如何把握小组合作学习设计的时机
2018-06-19广东恩平市年乐学校郑美金
广东恩平市年乐学校 郑美金
合作学习理论认为:合作的价值就在于通过合作实现学生间的优势互补。教师要善于选择合作的时机,因为不是所有内容都需要合作的,教师要根据教学内容、学生实际和教学环境条件等,选择有价值的内容、有利的时机和适当的次数让学生进行合作学习。注重选择小组合作学习的时机,主要体现在新旧知识衔接处,在实验操作时,在揭示知识的重难点、发现规律性知识时,在解法多样化需进行优化时,在辨析易混淆的概念时,在解决开放性问题时等等,我都放手让学生合作探究,精心设计合作学习内容,通过合作交流,让学生的思维得到启迪,思路得到开阔,从而培养学生的协作精神和创新意识。
一、在新旧知识联结处设计合作学习
“联结”指沟通知识体系,巧妙融合各种相关的知识经验,把知识放在更广阔的背景下进行教学,以旧拓新,这样能更好地对知识间的差异进行对比,让知识更有生气,更立体丰满。例如在教学《比的基本性质》时,在学生掌握了比的各部分名称及比的基本性质后,安排小组合作,合作学习问题设计如下:
(1)什么是商不变规律?试举例说明
(2)什么是分数的基本性质?试举例说明
(3)填表格
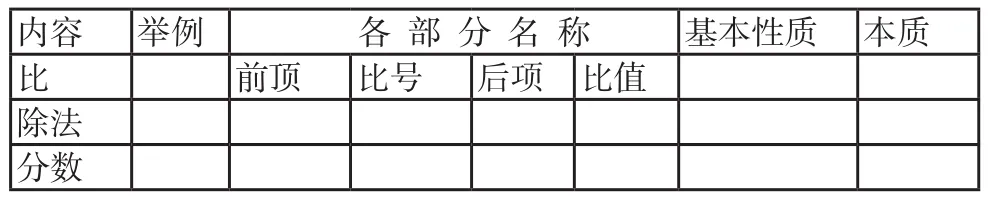
内容__举例_ 各 部 分 名 称 基本性质__本质__比 _____前顶__比号__后项__比值__________________除法__________________________________________________分数__________________________________________________
在新旧知识的联结处的合作学习不仅强化了知识间的横向联系,促使知识的融会贯通,同时了也能让学生多视角地理解知识、分析和应用知识,领悟数学内部知识间的融合关系,触类旁通,达到举一反三的效果。
二、动手操作时,开展小组合作学习
动手操作是小学生获得感性认识、发现数学关系的重要途径,也是激发学生探究欲望的重要载体。例如在教学“三角形的认识”时,发给每个学生2厘米、4厘米、5厘米、6厘米、8厘米的小棒,任取其中三根首尾相连围成一个三角形,6人小组合作学习。过程设计如下:
1.自主摆一摆,哪些能摆成三角形、哪些不能?为什么摆不成三角形呢?
2.和小组同学说一说、并分类填写好表格。
3.你发现了什么规律?并举例验证。
学生在操作的基础上发现不是任意三条小棒都能围成三角形,通过分类,找边与边之间的关系,发现三角形任意两边之和大于第三边这个规律,学生经历了感知、疑惑、思考、探索、发现等知识生成、发现、验证的全过程,体验了“纸上得来终觉浅,绝知此事要躬行”,理解深刻,教师教得轻松,优化了课堂教学效果。
三、把握本质,在知识学习的关键处设计合作学习
在小组合作学习中,教师将关键知识点转变为探索性的问题点、能力点,通过对知识点的设疑、质疑、解释,从而激发学生主动思考,逐步培养学生的探究精神以及对教材的分析、归纳、演绎的能力。探究的问题要能启发学生思维;问题不宜太多、太碎;问题应引导学生阅读思考;问题或者说知识点的呈现要尽量少用一个一个填空的方式,避免学生照课本填空,对号入座,抑制了学生的积极思维;问题的叙述语应引发学生积极思考,积极参与。如你发现了什么?你判断的依据?你的理由等。多用“想一想”“议一议”“试一试”“练一练”等问题情景去设计学习过程,让学生在学案的主线下进行自学,让学习提纲成为自主学习指导的老师。
四、在发散式思维和开放式习题处,开展合作学习
在教学活动中,教师要充分尊重学生个性,给学生以独立思考的时间和空间,在探索中形成自己的观点。
在答案开放的练习题中设计合作学习。在数学教学中设计开放性练习,给学生提供了一个充分表现个性、创新的空间,让学生自己动手、动口、动脑,让学生自己去发现问题和解决问题。例如:在讲完“三角形的分类”后,教师便举出一个装着三角形的纸袋,使三角形只露出一个角,让学生判断是什么三角形。当露出的是直角或钝角时,学生判断是直角或钝角三角形;而当露出的是锐角时,同学们则无法判断这个三角形是什么样的三角形,并且无法说出判断的理由。这时教师可以适时地加以点拨、引导,结合学习的三角形的特征让学生展开广泛的讨论,这样一来,课堂气氛异常活跃,每个学生都能够各抒己见,展示自己的个性以及创新的一面。
五、整理复习时,开展合作学习
在整理复习的教学中,教师以小组合作形式充分调动学生联系新旧知识,把自己学习过的相关知识形成完整的认知结构,从而进一步提高学生对这些知识的理解和掌握水平。例如在学完《比例》这一单元时,我设计这样的学案帮助学生整理正反比例相关知识:
1.什么是成正、反比例的量?它们的关系式是什么?试举例说明。
2.正、反比例关系的相同点和不同点各是什么?并填好表格。
正、反比例关系比较
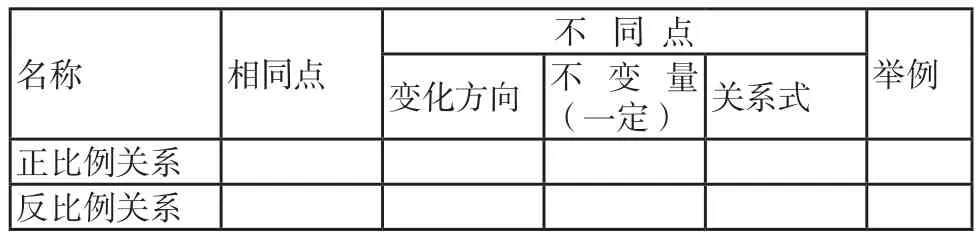
_________不 同 点_________名称 相同点(一定)关系式正比例关系____________________________________________反比例关系____________________________________________举例变化方向 不 变 量
3.两种相关联的量,不成正比例关系就成反比例关系吗?还有其它关系吗?试举例说明。用图表形式表示出来。
4.各小组列出正、反比例的应用题各一道,
5.选做题:解答下面的应用题。修一条2400米的路。原计划40天完成,每天修60米。实际4天修了300米,照这样计算,实际修完这条路要多少天?(用正反比例解答)
总之,在数学教学中适时适度有选择性地开展小组合作学习,使小组合作学习成为学生的探索、交流、展示的平台,使学生在探讨与辨析中擦出思维的火花,开阔了视野,拓宽了思路,有效地促进学生的语言表达能力、协作能力、创新能力、评价能力的提高,使课堂教学真正成为全面推进素质教育的主渠道。
