对一道书本习题改编的思考
2018-06-19浙江省杭州市淳安县大墅镇初级中学占宪辉
浙江省杭州市淳安县大墅镇初级中学 占宪辉
一、问题的提出
要深化落实新课程的标准,作为新时期的教师要学会利用好教材的资源,理解其本质,并对资源进行适当的改编,以凸显其数学本质。
初中数学中,研究线段之间的数量关系往往要借助全等三角形或相似三角形来进行,而全等三角形的构建往往是借助图形的变换而得来,其中包括旋转变换、平移变换、轴对称变换等等,本文就借教材中的一道习题通过适当的改编,凸显旋转变换在探究线段之间的关系,图形之间关系中的数学本质。
【原题呈现】
如图,E是正方形ABCD的AD
边上一点,延长BA至点F,使BF=DE,连结CE,CF.能通过旋转△DEC得到△FBC吗?请说明理由.
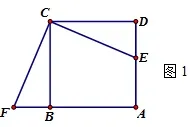
解答:能.理由:由已知,BC=CD, BF=DE,∴Rt△FBC≌Rt△EDC.∴∠DCE=∠BCF.∴∠FCE=∠DCB,CF=CE.所以把△DEC绕点C按顺时方向旋转90°时,CE与CF重合,DC与BC重合,也就是得△FBC.
通过解答让学生明确三角形旋转变换的条件:一是有旋转中心,二是各部分按同一方向转动同一角度。但是如果这道题目就到这里为止,显然没有发挥出它应有的价值,特别是发挥旋转变换在解决三角形和四边形中线段之间关系中的作用,笔者根据有关习题改编的方法,通过通过将条件和结论互换、增加条件、减少条件、改变图形等一系列改编,进行横向的拓展和纵向延伸.
二、对该题的改编
(一)结论和条件互换——用好旋转三角形的性质
【改编1】
如图1,将Rt△DEC旋转绕着点C顺时针旋转90度,得到Rt△FBC,延长DE和FB交于点A,你能发现四边形ABCD是什么特殊的四边形?请说明理由.
解题分析:在图形没有改变的条件下,显然学生能够猜想到这是一个正方形,而且根据正方形的判定方法,显然只要先证明它是矩形再根据邻边相等,就可以得出。而这些结论的得出都需要利用好旋转变换的性质.(具体证明过程略)
(二)增加条件——抓准旋转的三角形
【改编2】
如图2,在正方形ABCD中,点E,G分别在边DA、BA上,且∠ECG=45°.
(1)将△CDE绕着点C顺时针旋转90°,得到△CBF,试分析BG与DE的和与EG有什么数量关系?
(2)如图3,若点E在AD的延长线上,G在BA的延长线上,∠ECG=45°,则BG、DE、EG三条线段还有原先的数量关系吗?如果有加以说明,如果没有,请写出新的数量关系.
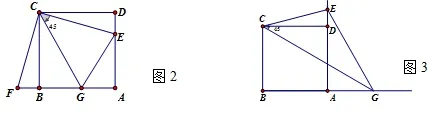
解题分析:第(1)小题由∠E C G=45°可知△FCG≌△ECG,从而得到EG=FG,而FG=BG+BF=BG+ED,因此BG+ED=EG .
第(2)小题,只是点E的位置改变到AD的延长线上,仍可以将△CDE绕着点C顺时针旋转90°,得到△CBF,由∠ECG=45°可知△FCG≌△ECG,仍可得到EG=FG,而此时FG=BG-BF=BG-ED,即EG= BG-ED.
(三)减少条件——构造旋转三角形
若将图1中的正方形部分隐藏掉.将原来的三角形的旋转变成了一条线段的旋转,这样虽然从图形上看是简单了,但对于线段之间数量关系的发现却增加了很大的难度,因此在解题中可以通过旋转将原图形补全来解.
【改编3】
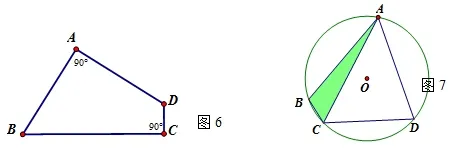
如图6,在四边形ABCD中,AB=AD,BC+CD=10,∠A=∠C= 90°,求四边形ABCD的面积.
【改编4】
如图7,在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.
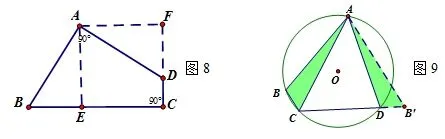
解题分析:引申3可以过点A作BC及CD所在的直线的垂线,垂足为E、F(如图8),由AB=AD,∠A=∠C= 90°可以证明△ABE≌△ADF,因此四边形的面积转化为正方形AECF的面积,再根据BC+CD=10,可得正方形的边长为5,面积为25.
引申4可以延长CD至B′使得DB′=BC连结AB′(如图9),显然△ABC≌△ADB,所以AC=AB′,由∠ACD=60°可得△A B′C为等边三角形,从而把四边形ABCD的面积转化为△A B′C的面积,由AC=1,可以求出△A B′C的面积为
(四)改变图形——重构旋转三角形
通过改编5已经发现,旋转不一定要在正方形中进行,正三角形中也经常可以借助旋转来解决,进一步可以探究出只要符合一定的条件均可以借助旋转来分析线段之间的数量及位置关系。
【改编5】
如图10,四边形ABCD中,AC、BD是对角线,△ABC是正三角形,∠ADC=30°,AD=3,BD=5,求CD的长.

解法分析:此题的解法较多,但不管什么办法都是借助三角形的旋转将两条已知线段和所要求的线段长放在一个直角三角形中利用勾股定理来进行计算,求得CD=4.现将几种利用旋转的解法图形呈现如下(具体解题过程略):


数学教育家弗赖登塔尔说过:“反思是数学思维活动的核心动力,没有反思,学生的理解就不可能从一个水平升华到更高的水平”反思可以深化对问题的理解,优化思维过程,揭示问题的本质、沟通知识间的联系、促进知识的同化和迁移、进而产生新的发现,是提高学生解题能力的重要途径。
