光栅光谱分布特性分析与讨论
2018-06-19张明霞令维军路飞平
张明霞,令维军,路飞平
(天水师范学院 电子信息与电气工程学院,甘肃 天水 741001)
1 问题的提出
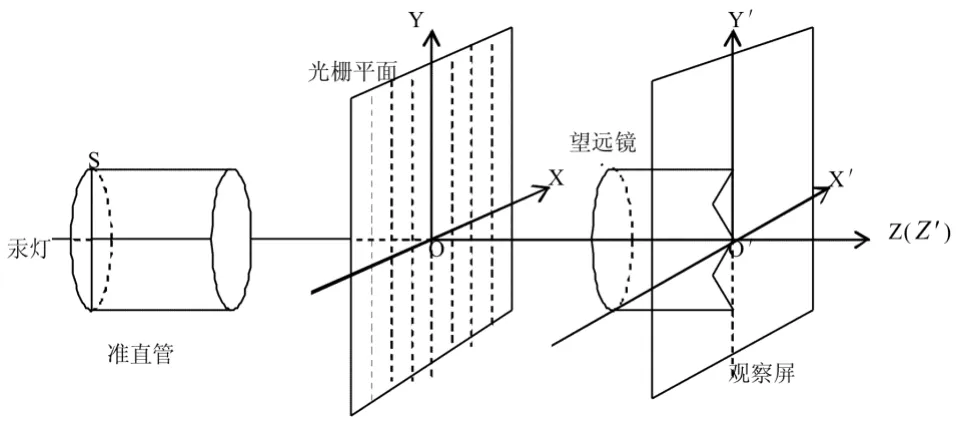
图1 光栅衍射实验装置示意图
光栅衍射实验是波动光学中非常重要的一个实验,图1所示为在分光仪上做光栅衍射实验时的简单装置示意图。[1]高压汞灯发出的复色光先经过准直管,准直管的左端为一狭缝S,可看作一缝光源S,它的方向可调,缝光源S位于准直管的物方焦面上,准直管后依次是平面透射光栅(简称光栅)及望远镜,通过望远镜可将在无穷远处所产生的干涉光谱重现在望远镜的目镜视场中。
笔者在实验教学中发现,将缝光源S绕准直管的主光轴旋转,观察到随着缝光源同步旋转的彩色的光栅光谱,说明谱线的分布特性和缝光源的位置有关,而缝光源的位置决定了光波通过光栅时的入射方式,即谱线的分布特性与入射光波的入射方式有关。缝光源S可看作无穷多个点光源的集合,准直管出射的光波并不是全部垂直入射或特殊斜入射于光栅平面,而是包含了多种入射方式(取决于狭缝的方向)。因此,实验中观察到的谱线随着光波入射方式的不同而产生复杂的变化,而国内大多文献均仅对垂直入射或特殊斜入射的光栅光谱分布特性进行分析讨论。[1-7]一般情况下,单缝衍射和多光束干涉两种效应共同对光栅光谱分布特性产生影响,但是单缝衍射仅对谱线的强度起调制作用,谱线的位置数目是由多光束干涉决定的。下面,笔者综合考虑缝光源的位置、光波通过光栅时的入射方式及光栅平面上光波相位分布情况,采用矢量图解法仅对多光束干涉场进行分析及计算,得到多光束干涉光强分布的一般公式,并通过多光束干涉光强分布的一般公式解释实验中观察到的随着缝光源同步旋转的光栅光谱分布特性。
2 多光束干涉光强分布公式推导
2.1 矢量图解法求多光束干涉光强公式
图2为多光束干涉光路示意图,光栅平面内有N个互相平行的单缝在空间周期性排列,单缝宽度为a,d为相邻单缝对应点的间隔。暂不考虑光波通过单缝衍射,即不考虑单缝对谱线强度的调制作用,假设每条单缝发出的光波在θ方向在P点产生的振动振幅为均为a0,得到N个振动,然后把这N个振动叠加起来,即得到N个振动在P点叠加后的总振幅Aθ.下面用矢量图解法来计算N个振动在P点叠加后的振动总振幅Aθ.

图2 多光束干涉光路示意图
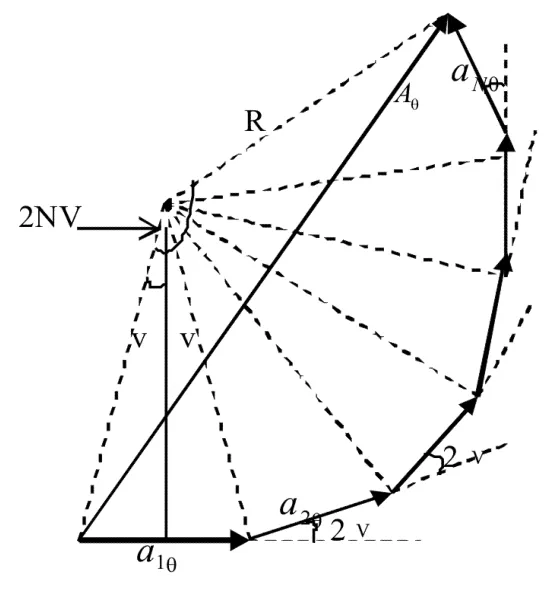
图3 多光束干涉矢量合成图
如图3所示为多光束干涉矢量合成图,计算来自N条缝合成振动的叠加,需要计算它们之间的相位差,而合成振动间的相位差同N条缝对应的发出的衍射线间的相位差Δφ是一样的,为了简便运算,将两相邻狭缝间的对应点在θ方向达到P点时的相位差的一半记为ν,令

△L为两相邻狭缝间的对应点在θ方向达到P点时的光程差。将N条单缝在θ方向达到P点时的振动矢量a0首尾相接,辐角依次增大2ν,排成正多边形的一部分,当参与叠加的缝的数目增加时,正多边形的一部分可看作一段圆弧,对应的圆心角为2NV,半径为R,a0对应的圆心角为2V,由图中的几何关系知

由(1)和(2)式可得P点的合振幅为

则多光束干涉光强分布公式为

2.2 缝间干涉因子分析及计算
由公式(3)知,多光束干涉光强分布取决于多光束干涉因子多光束干涉因子随着v的变化而变化,v取决于光栅平面上光波相位的分布,而光栅平面上光波相位的分布情况是由光波的入射方式决定的,缝光源的位置不同,光波通过光栅的入射方式就不同。将缝光源S绕准直管的主光轴旋转时,缝光源S上的每一个点光源通过平行光管以不同的方式入射于光栅平面,如图4所示为任意一个点光源通过平行光管后一般斜入射于光栅平面时的的光路图,和Y轴平行的虚线代表单狭缝,光栅平面内的斜虚线为分别过A和B两点的等相位线,即平面光波等相位面和光栅平面α的交线。A和B两点为相邻狭缝的对应点,过A点作过B点的等相位线的垂线,垂足为C点,B和C两点的相位相等,A和C两点在入射面β与光栅平面α的交线上,过A和C两点的入射线和n轴间夹角为θ0(n轴在β平面内且于直线----AC垂直)。

相邻狭缝上对应点A和B在θ方向发出的波线在P点产生的光程差为A和C两点在θ方向发出的波线在P点产生的光程差,过A点作入射线2的垂线,垂足为D,设则A和C两点在θ方向发出的波线在P点叠加的光程差为其中,光程差dsinθ对平面光波在三维空间所有的入射方向都是相等的(如图2所示);d0sinθ0是平面光波到达光栅平面时相邻狭缝对应点光波的光程差,当平面光波的入射方向改变时,d0和θ0同时发生变化。±号表示入射线和出射线在光栅平面法线同侧时取+号,反之,取-号。
在直角△ABC中,d0=dsinφ,其中φ为过B点的等相位线与X轴间的夹角,利用几何关系,我们不难证明φ角的大小取决于平面光波的入射方式,这一点笔者在文献[8]中分析单缝衍射时做过讨论。那么,A和B两点在θ方向发出的波线在P点产生的光程差为
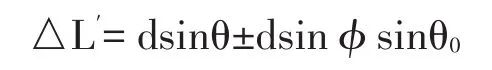
同时考虑A和B两点在θ方向在P点产生的相位差为2πΔL λ,则
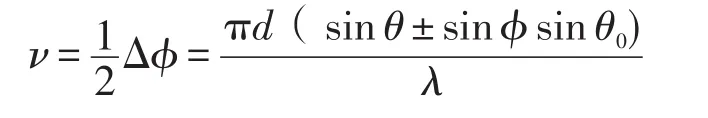
将v代入多光束干涉因子公式,可得多光束干涉因子在光波任意斜入射条件下的一般形式为
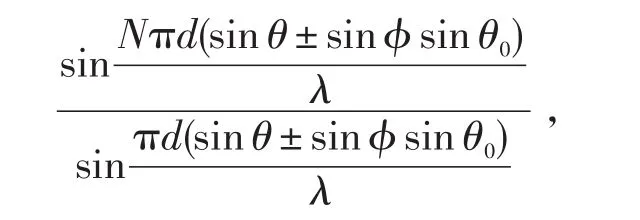
将此干涉因子代入光强分布公式(3),得到平面光波在任意斜入射于光栅平面时的多光束干涉光强分布公式为

其中,为光栅平面内过B点的等相位线与X轴间的夹角,θ0为入射线和n轴间的夹角,θ等于衍射角。
3 利用多光束干涉光强公式解释光栅光谱的分布特性
由公式(4)知,光波在一般斜入射条件下通过光栅平面时,多光束干涉因子拓展为
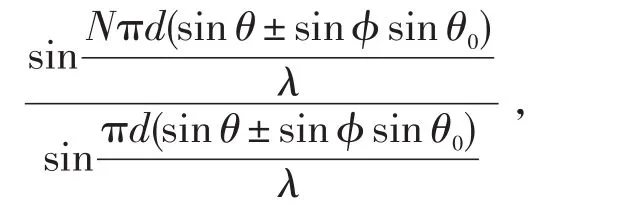
实验中观察到的各级谱线分布特性是由多光束干涉因子决定的。下面利用多光束干涉因子分析各级谱线的强度、位置、数目等分布特性。
当

的位置,即dsinθ±dsinφ sinθ0=Kλ,当K=0时,相邻两缝光程差为零,谱线为零级主极大,根据几何时,多光束干涉因子的分子和分母同时为零,此时多光束干涉因子取极大值N,谱线的各级主极大强度均相等,Ip=N2I0.各级主极大谱线出现在光学观点,物像之间具有等光程性,因此零级谱线就出现在几何像的位置,物和像相似,再根据衍射理论,其它各级谱线和零级谱线平行,这就解释了光栅衍射实验中当缝光源S绕准直管的主光轴旋转时,光栅光谱随着缝光源同步旋转,说明谱线的位置和缝光源的位置有关。谱线的极大值数目也是由多光束干涉因子决定的,当θ=900时,sin900=1,由计算知,K的极大值为K的极小值为由此可确定实验中可以观察到的主极大谱线的总数目。由以上分析可知,多光束干涉因子决定了各级主极大谱线的强度、位置、数目等分布特性。
4 结束语
由以上分析及计算知,多光束干涉光强公式主要取决于缝间干涉因子而缝间干涉因子取决于光栅平面上光波的相位分布,考虑缝光源上每一个点光源S处于准直管的物方焦平面上不同方位时,光栅平面上光波的相位分布不同,缝间干涉因子拓展为进而得到全面的多光束干涉光强公式(4),利用此公式可以解释实验中所出现的随缝光源同步旋转的光栅光谱的分布特性。
[1]杨述武,王定兴.普通物理实验·光学实验[M].北京:高等教育出版社,2005:119-123.
[2]蔡履中.光学[M].北京:科学出版社,2007:242-246.
[3]姚启均.光学教程[M].北京:高等教育出版社,2008:92-96
[4]张明霞,赵玉祥.一般斜入射情形下平面透射光栅衍射现象分析[J].天水师范学院学报,2015,35(2).
[5]申志荣.平行光斜入射光栅时的衍射特性研究[J].陕西科技大学学报,2003,21(5).
[6]郑曙东.非正入射条件的光栅衍射实验[J].青海大学学报(自然科学版),2005,23(4).
[7]段萍,刘金寿.光栅衍射条纹分布的探讨[J].大连大学学报,2004,25(4):12-13.
[8]张明霞.夫琅禾费单缝衍射光强分析与探讨[J].湘潭师范学院学报,2009,31(4).
