活用教材资源促进意义建构——《平均数》教学案例（一）

徐金春

【教学内容】

人教版四年级下册第90～92页。

【教学过程】

一、找准起点，明确目标

1.直接揭题。

师：今天，我们学习“平均数”（板书）。

2.交流引入。

师：同学们听说过平均数吗？你认为，什么是平均数？（学生发言，教师针对性评价）

师：看来，对于平均数，同学们已经有了一些了解。这节课，我们将通过一些活动来加深对平均数的理解。

【思考：生活中，“平均数”是一个较常用的数学概念。鉴于四年级学生对平均数的认识有一定的经验，通过直接揭题和请学生谈谈对平均数的已有认识，能帮助教师了解学情、找准起点，体现“数学学习是基于经验的持续生长”的施教理念。】

二、实践体验，建构意义

1.读信息，提问题。

师：请看大屏幕，这是某小组四位同学在“我是环保小卫士”活动中收集水瓶的情况。（出示教材例1主题图）从图中，你能获得哪些数学信息？

生：我知道了每个人收集的水瓶数量。

生：小明收集的最多，有15个；小亮收集的最少，是11个。

（根据回答，课件相机出示）

师：真棒，我们获得了这么多数学信息。那么，你能提一个与“平均数”有关的数学问题吗？（学生提问，课件出示：这个小组平均每人收集了多少个水瓶？）

【思考：“能获得哪些数学信息？”“能提一个与平均数有关的数学问题吗？”两个平常的学习指令，打开了学生自主收集信息、有效提出问题的“窗口”，有利于其“四能”的逐步发展。】

2.探策略，明原理。

师：对，这个数学问题要求的就是“平均数”。（课件在问题旁边出示：平均数）

师：会解决这个问题吗？请大家用自己喜欢的方法在作业纸上解决。（教师着重收集两类作业：第一类是“移多补少”，借助展台交流；第二类是“先合后分”，请学生板演解答）

（1）交流“移多补少”策略。

师：（投影作业后）你是怎么思考的？

生：小红比小兰多2个，小红给小兰1个，俩人就相等了。小明比小亮多4个，小明给小亮2个，俩人就相等了。

师：为什么要“多的移给少的”，而不是“少的移给多的”呢？

生：如果“少的移给多的”，那么少的就更少，多的就更多，不会“平均”了。

师：很好，我们通过“移多补少”（板书）达到了“每人一样多”的目的，求出了平均数。（课件演示：“移多补少”的动态过程）

（2）交流“先合后分”策略。

师：（指着板演的算式）（14+12+11+15）÷4=13，谁看懂了？

生：先算出“四个人一共收集了多少个水瓶”，再平均分成四份，就能得到平均数了。

师：很好，这种算法我们可以称为“先合后分”。（板书，课件动态演示：四个人收集的水瓶先汇总，再重新平均分成四份）这样算的数学道理，其实就是我们二年级学过的“平均分”。

【思考：这个过程充满了自主性与生成味。“移多补少”是平均数形成的背景，“先合后分”是平均数运算的方法，这两者都得到了充分呈现。值得一提的是，在交流“先合后分”策略的过程中，教师通过课件动态演示再现了蕴含其中的“平均分”本质，沟通了新旧知识的内在联系，让数学生长更稳妥、更牢靠。】

3.辨内涵，悟本质。

师：平均数为“13个”是否说明，他们每个人都收集了13个水瓶呢？

生：不是的，但都与13个很接近。

生：虽然不是13个，但都在13个左右。有的比平均数大，有的比平均数小。

（根据回答，课件出示表示平均数的红线，引导学生感受平均数的虚拟性）

师：妈妈知道小明在收集水瓶。同学们，你认为妈妈会比较关心小明的哪些情况？（根据回答，课件创设对话情境、并出示两个问题：你收集了多少个？你们整个小队的情况怎样？）

师：对于第一个问题，大家都知道小明会告诉妈妈“我收集了15个”（课件出示）。对于第二个问题，小明准备了两种回答。如果你是妈妈，更想听哪一种？（课件出示：A.我们一共收集了52个。B.我们平均每人收集了13个。）

生：更想听第二种回答。这样，妈妈就能知道小明收集的瓶子数超过了小组的平均水平。

生：我也认为是第二种回答，这样就能看出小明的“战况”很不错。

师：有道理。平均数能让我们看出全组同学的整体水平。（板书：整体水平）

【思考：针对“平均数是13”这个解答结果，教师通过即时追问，使学生明确了平均数的虚拟性。在此基础上，教师非常巧妙地设计了一个延伸情境，组织学生共同讨论“妈妈会比较关心小明的哪些情况？整个小队的情况怎样？”帮助其最终把握“平均数表示一组数据的整体水平”的本质属性。教学，由此走向了深入。】

三、灵活运用，感悟价值

1.基本应用。

师：顺利解决了“收集水瓶”的问题，我们来解决“踢毽比赛中的问题”。（课件出示图1）男生队和女生队，哪个队的成绩更好？

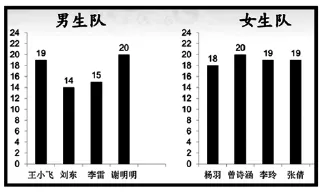
图1

（学生独立思考、交流汇报。教师板书：一对一比；比总数；比平均数。为丰富学生的直观感受，课件出示表示男、女队平均数的两条红线）

2.变式应用。

师：老师在统计男生队的成绩时，漏了“孙奇同学的成绩”，他踢了22个（课件演示图2：男生队条形图中补上“孙奇22个”）。现在，你认为哪个队的成绩更好？怎么比更合适？

图2

生：人数不同，“一对一”的方法不能比。

生：比两队的总数。（随之招来反对声：人数不同时，比总数不公平）

生：用平均数比较。（学生算出男生队的平均数是“18”，发现女生队依然领先）

师：是什么原因导致男生队的平均数升高了呢？孙奇的“22个”是所有人中最好的，为什么男生队还是失败了呢？（学生思考回答，教师点评指导）

3.拓展应用。

师：如果男生队和女生队要打成平手，即男生队的平均数也是19个，孙奇至少要踢几个？

（学生思考并尝试解决：19×5-68=27）

师：假如孙奇踢的个数比27个多，你认为男生队的平均数会发生怎样的变化？如果孙奇踢的成绩很差，比如只有7个，这时男生队的平均数又会发生怎样的变化？

师：看来，当其中一个数发生变化时整组数据的平均数就变了。

【思考：教师有意微调了教材例2的呈现方式及个别数据，使学习材料的思辨空间更大。学生经历了“4个对4个”向“5个对4个”的情境变换，再次体会“平均数反映整体水平”的基本特点。随后，教师继续变换情境，带领学生参与“已知平均数、求某个具体数据”的逆向练习，并让学生切身体会“平均数会根据个别数据的变化而变化”。整个过程，“变式”发挥了重要作用，增加了学习活动的“厚度”。】

四、总结收获，梳理过程（略）

五、联系实际，综合思辨

师：小东喜欢游泳，他的身高为1.4米。现在有一个水深1.1米的儿童泳池和一个平均水深1.1米的池塘。你认为，小东到哪里去游泳相对比较危险？为什么？

（先让学生根据自己的理解在纸上画一画示意图。在展示、交流、汇报的基础上，课件呈现池塘、游泳池的截面图，再次强调平均数所反映的是“整体水平”）

【思考：练习中，通过对两个“1.1米”的对比分析，进一步突出了“平均数反映整体水平”的核心要义。另外，让学生通过画图来诠释思考过程，有利于其几何直观能力的发展。】