收与放的交融———算法多样与算法最优——以苏教版《十几减九》为例

吴中杰

《数学课程标准（2011版）》提出：“计算教学中，不仅要创设情境，还要尊重学生的个性，鼓励算法的多样化。”这使传统教学模式下以教师为中心的课堂，逐步向以学生为中心迈进，给了学生更多的思维空间和创造机会。学生在自主探索创新之中，其思维得以开拓，个性得以张扬，也契合《数学课程标准（2011版）》提出的“不同的人，在数学上得到不同的发展”的理念。在这种背景下，课堂上学生思维更加活跃，各种创新的素材也不断涌现，各种各样的算法也得以出现，达到了算法多样化的目标。那么，在多样化的算法中我们是否还需要寻求最优的算法呢？何种方法才是最优呢？下面，笔者结合《十几减九》一课做简单的分析。

一、课本最优是否就是最优

首先，我们对教材做简略的分析，找寻教材的最优。先对“想一想，做一做”第一题进行分析，教材给出了两个算式：“12-9=”和“16-9=”并用小棒进行了表示引导，12-9以10根小棒为一堆，另外一堆则为2根；16-9也是以10根小棒为一堆，另外一堆为6根，感觉上教材是想强调破十法，也是很多教师认为本课最优方法是破十法的原因。那接下来，我们再来看第二题，教材也是给出了两个算式“15-9=”和“17-9=”，而15-9给出的示意图是9个正方体为一堆，另外一边则遮住了，那就用“？”表示，17-9的示意图也是以9个为一堆，另外一堆并不知道。不知看到这里，你是否发现了教材的深意，教材突出强调了“9加几”，这里教材则明显地提示了本课应当以“想加法，做减法”为最优算法。到了这里，可能部分教师还是有疑问，为何是“想加法，做减法”呢？那不妨我们继续往下，再来对教材进行解读。我们看第三题，9+2=，11-9=，9+5=，14-9=，9+9=，18-9=。而在课后的练习1中也有体现，练习1中的第一题9+？=12，第二题 9+？=15，15-9=，9+？=16，16-9=，9+？=17，17-9=则都是侧重在“想加法，做减法”的算法上，想必到了此处，再对教材进行认真阅读、分析、比较、思考后，教材的意图便跃然纸上。

由此可见，对于本节课，教材意图是让学生掌握“想加法，算减法”的运算方法，即是教材中所给出的最优化算法。而往往执教的教师也都一味地去强调这种算法，却并未关注学生是否能够理解和接受。教师虽然是按照《数学课程标准（2011版）》和教材意图进行教学，但由于学生的年龄和认知水平的局限，可能教材所提出的“想加法，算减法”对于一年级的学生来说，过于偏高。而本节课中，学生在已有的知识经验的基础上，所创造的多样化算法：“逐个递减”、“破十法”、“平十法”等方法相比较于教材所要求的“想加法，算减法”来说，计算思维层次可能相对较低。而通过本节课的教学，对于各种算法的分析比较，学生都已基本掌握了一种适合自己的算法，但对于“想加法，算减法”能够熟练掌握并运用的学生并非很多。这是否是教师的教学失误？算法最优并未得以实现呢？

笔者认为，教师传授算法时按照课本意图的教学自然并无过错，但如果教师一味地去强调课本的最优，而忽略了学生的学情，强行将教材最优算法灌输给学生，而忽略学生自身的算法体验，那本节课的教学可能是毫无意义的。学生没有接受“想加法，算减法”，虽然从表面上看他们还未实现算法的最优，但若教师安排了一定的教学活动，让学生在通过自主动手操作、分析比较、整理归纳后，在其原有的算法基础上，发现自身算法的不足，并将自己最初的算法进行一定的完善，得到了一种最适合自己的算法，并能够对后续问题进行处理解答。那我想，本节课的教学无疑已经实现了最优。

根据学生的学情和实际，教材的最优并非是学生的最优。而真正的最优应该是学生在多样化的算法中，掌握基本的算法，体验知识的建构，在对多样化的算法有了一定的理解、感悟的基础上，再通过教师的引导，对多种算法进行比较、分析、归纳、感悟后，进行自我完善，悟出属于自己的最优算法。只有通过自己的探索发现，改善自身的不足，吸收较为先进、简便的方法，补足自身，才能得到属于自身最优的算法。

二、算法多样化与算法最优是否矛盾

在当前“多样化算法”风靡的背景下，许多教师对“最优算法”是否有必要提出产生了疑问。既然都提倡了“算法的多样”，又何必再去进行“算法的优化”呢？笔者认为，算法的多样化是一种态度，一个过程。最优的算法是算法多样化的归宿，是学生自我反思，自我完善的产物。《数学课程标准（2011版）》是“鼓励”算法的多样化，而并非强制要求多样化。而往往我们的课堂教学中，只注重了“算法的多样化”，一味地寻求不同的算法，而忽视了算法多样化的本意。在一味的寻求过程中，学生利用已有的知识经验，创造出的方法可能并不科学、合理，而计算过程可能也十分复杂。甚至有些学生思维还处于混乱之中，虽然给出的算法可以得出结果，但可能并不能讲出具体的意思。而真正的多样化算法，也应当建立在清晰思维、合理逻辑、科学简便的基础之上，而并非囫囵吞枣，将所有算法都囊括其中。而在如此多的算法之中，有些算法的思维水平层次可能过于低，对于后续的学习并无帮助。如果不对其进行优化，那学生可能永远掌握着自己原先所拥有的算法，便会导致学习的两极分化，使差生越来越差。学生的思维也无法得以发展。因此，多样化算法后，应寻求最优，让学生在寻求的过程中得以自我完善和发展，思维能力得以提高。

三、情境融入教学，算法得以优化

苏教版一年级教材中，对于13-9的算法给出了三种预设的学生的算法：

1.平十法，将9拆分成3+6，再用13-3，然后用10-6。

2.破十法，将13拆分成10+3，再用10-9=1，再用1+3。

3.想加法，做减法，13-9，我们先想到加法，9加几才等于13？

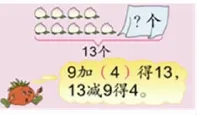
而往往在实际教学中，低年级的学生可能还会给出第四种回答，用13一个一个地进行减法，一共减9次，这样也得到了结果。那这样我们对于13-9则有了四种不同的计算方法。此时，我们的教学便已经达到了算法的多样化目标。

在这四种算法中我们可以明确地看出四种方法的层次性，对于一个一个减去的方法，显然相比于“平十法”、“破十法”而言，此种方法的思维层次是最低的，而“想加法，算减法”相对而言其思维层次则显得过高。但相信经过教师的点拨，学生自己的动手操作，四种算法中学生必能对一种方法进行掌握和应用了。而教师往往在教学时便顺水推舟，可能只是简单地对学生的方法进行评价后，便进入了习题的巩固之中，并未对多样化的算法进行进一步的详细分析，给予学生更多的思考，让学生体会各种算法的特点，并与自身的方法进行比较、归纳，从而将自身的算法得以完善。在具体教学中，执教者到底应当如何在多样化的算法中，帮助学生对算法进行优化呢？下面笔者结合《十几减九》一课的教学，进行简单的教学设计。

（1）课前导入。

建构主义学习理论认为，学习的过程是学习者主动建构知识的过程，学习者以原有的知识经验为基础，通过与外界的相互作用来建构新的知识结构。因此，本节课的课前导入部分可用旧知导入，教师可先带学生复习20以内进位加法，然后提升难度，设计？+9=12，？+8=12……此类加法问题，在复习旧知的同时帮助学生巩固原有知识，又为之后本节课的“想加法，做减法”教学做铺垫。

（2）结合情境，优化算法。

结合教材主题图，将算法多样化教学融入教学活动之中。教材第一幅图是平十法，将一筐13个桃子，先拿出了3个，后又拿出了6个；第二幅图是破十法，从13个桃子中拿出10个，剩下了3个，再从10个中拿掉9个；而第三幅图，则是给出了一堆9个桃，另外一堆桃子被遮挡住了，让学生思考有了9个桃子，再加几个才是13个。这里教师可以让学生利用简单的学具圆片来代替桃子，自己动手将课本所给的图片进行实际的操作，以帮助学生从实际情境中去理解真正的算理。

然后教师可以根据各种不同的算法的特点，创设情境性练习。

①针对一个一个减算法进行如下设计：小猴买了12个桃子，每天吃1个，这样连续吃了9天，你知道小猴子还剩几个桃子没有吃吗？这时学生都会以各自所掌握的不同的方法进行解答，而有的学生可以很快解答得出结果，有的学生则非常慢，这就体现了算法之间的差异，让那些用逐一减的学生得以思考，进而对自身的算法进行优化，实现初步的最优。

②针对破十法：小猴妈妈出门了，给小猴留下了2堆桃子，一堆有10个，另外一堆有6个，妈妈嘱咐小猴，今天一天只有这些桃子能吃，可是贪吃的小猴一下子就吃了9个桃子，它今天还能吃几个桃子呢？学生在这样的引导之下就能发现我们可以先用10-9再加上6得到结果，好像相比于第一种方法简化了很多。确实“破十法”对于低年级的学生来说是比较容易理解和接受的，大多数学生在优化自身算法后便也能熟练地运用破十法进行问题的解决。

③针对平十法：小猴一个人在家里无聊，于是打电话找来了它的好朋友小花猫来陪它玩，小花猫给小猴带来了15个桃子，小花猫不喜欢吃桃子，所以只吃了3个，而小猴可喜欢吃桃子了，所以小猴吃了6个，同学们知道它们两个吃完后还剩几个桃子吗？平十法可以让大多数学生都掌握、运用，并且能让学生自主动手研究学习，计算时也相对简单、快捷。

（针对②③的教学设计，笔者建议可以制作适当的PPT，进行动画演示，以具体的动态实物为例，可以让低年级的学生更好地把握题目意思）

④针对想加法，算减法：小猴妈妈回来了，还带回来两篮桃子，妈妈告诉小猴，这次一共带回来17个桃子，并告诉小猴子一个篮子里装了9个桃子，那另一个篮子装了几个呢？你能帮助小猴算一算吗？这个方法看似简单，但对于低年级的学生来说显然其思维水平更上了一层楼，要求学生能将加法进行逆运算，对于一些基础并不是很扎实的学生来说要求过于偏高了。

在进行完这些题目的练习、讲解后，教师可以帮助学生一起分析、比较、归纳各种算法的特点，也可以让学生自己说说，然后选择自己喜欢的算法和小组成员交流一下所选择的算法。相信通过这样的自我完善的过程后，学生在保留了自己个性化算法的同时，也对其他的不同的算法有了新的体会和认识，对自己本身算法的缺陷也得到了弥补，找到了一种属于自己的最优算法。到此，本堂课的教学目标也已完成——让学生在张扬个性后得到多样化算法，并对自身的算法进行改善、优化，最终找到了自己的初步算法归宿。

算法的多样化是“放”，算法的优化是“收”，教师只有在这一收、一放之间，做到收放自如，才能在多样化的背景下，让学生在彰显个性的同时，又能得到进一步的发展，在培养创新性思维的目标中，又有所改进和提高。唯有“多中择、因人择、因材择、择而优、优而用”，才能让多样化的算法和最优的算法得以相辅相成。