磁流变减振器力学模型校验及天棚ON-OFF控制
2018-06-19张进秋彭志召
彭 虎, 张进秋, 张 建, 彭志召, 张 杨
(1. 陆军装甲兵学院装备保障与再制造系, 北京 100072; 2. 陆军装甲兵学院车辆工程系, 北京 100072;3. 驻674厂军代室, 黑龙江 哈尔滨 150056)
车辆悬挂系统用于支撑车体,缓和路面不平度冲击和衰减振动,以达到隔振和减振的目的[1]。目前,可控悬挂主要分为主动悬挂和半主动悬挂2类,其中:主动悬挂减振性好,但控制能耗大、成本高且不易维护[2];相比之下,半主动悬挂通过变阻尼实现减振,能量不直接参与振动控制,具有能耗低、阻尼连续可调、易于控制及“失效-安全”特性等优点,其控制性能接近主动悬挂,得到了广泛关注[3-4]。
磁流变减振器(Magneto-Rheological Damper, MRD)是一种阻尼连续可调的新型变阻尼减振器,其利用内装的磁流变液(Magneto-Rheological Fluid, MRF)在外加磁场作用下发生流变效应的特性改变阻尼力,实现变阻尼[5]。MRD响应迅速(通常为毫秒级)、体积小、能耗低,在控制失效时黏滞阻尼可充当被动阻尼起到减振作用,具备“失效-安全”特性,具有良好的发展前景[6-8]。然而,对MRD实现控制需要建立相应的力学模型,常用的MRD力学模型有Bingham模型、Bouc-wen模型及多项式模型等。其中:Bingham模型表达式简单、意义明确,但模型精度稍差,难以描述MRD阻尼力-速度的滞回特性;Bouc-wen模型可准确表示MRD阻尼力-速度的滞回特性,但模型结构复杂、参数多,且部分参数表示的物理意义不明确;多项式模型可通过提高拟合阶数来提高模型精度,不仅可反映MRD阻尼力-速度的滞回特性,且便于求解MRD逆模型[9]。此外,对力学模型校验是检验其准确性的重要步骤,但目前并未引起足够重视,仅通过简单地对建立的模型与试验数据得到的阻尼力曲线之间的拟合度进行比较判断科学性不强,因此亟需一种科学的力学模型校验方法。
鉴于此,笔者以某轻型军用轮式越野车为研究对象,首先设计阀式MRD并利用平板模型推导其阻尼力模型;然后,基于最小二乘法对试验数据拟合得到的MRD多项式力学模型进行校验;最后,采用天棚ON-OFF半主动控制算法对设计的阀式MRD的减振性能进行台架试验,以期为其在军用车辆上的发展和应用提供一定参考。
1 MRD建模及特性试验
该MRD主要由活塞、活塞杆、线圈及缸体等部分组成,图1、2分别为其结构图及实物图。图中:活塞由内阻尼活塞和外导向活塞组成,可缩短轴向尺寸;磁回路从导向活塞绕回,可减小漏磁;导向活塞上下两端开有MRF流通孔,阻尼缝隙采用环形缝隙式结构;浮动活塞式体积补偿装置用于补偿活塞杆占用的部分体积。
1.1 MRF模型
将MRF视为Bingham模型,则MRF的本构关系可近似描述为[10]
(1)

采用实验室自制的MRF,η=0.8 Pa·s,其剪切屈服应力τy与磁感应强度B的关系如图3所示。可以看出:正常工作条件下,MRF的磁感应强度一般为0.4~0.6 T,对应的剪切屈服应力约为23 kPa,满足使用需求。
利用MATLAB的cftool工具拟合τy与B的关系,可得
τy=-39B2+68B-1.3。
(2)
1.2 MRD阻尼力模型
该MRD工作模式为阀式,由文献[11]可知:将环形缝隙近似为平板模型带来的最大误差小于5%,因此采用平板模型推导阻尼力模型。图4为阀式平板流动工作模式示意图。图中:w为平板宽度;L为平板长度;h为缝隙高度;Q为MRF体积流量;Δp为压强梯度。建立坐标系xOz,其中:原点O在下平板的表面;Ox轴为MRF的流动方向,Oz轴为液体流动的垂直方向。
图5为平板间MRF的流速与应力分布示意图。图中:Ⅰ、Ⅱ、C分别为上、下梯度流速区和等流速区;v0为活塞运动速度;p为沿MRF流动方向的压强;u为MRF的流速;uC为C区域MRF的流速;h1、h2及hC分别为I、I+C及C区的宽度;δx为微元的单位长度。
根据图5可推导出压强梯度公式为
(3)
对式(3)两侧积分可得
(4)
式中:D1为常数。由τh1=τy,τh2=-τy及式(4)可得
(5)
(6)
在区域Ⅰ中,
(7)
将式(4)代入式(7),且令初值u(0)=0,则在0≤z (8) 在区域Ⅱ中, (9) 将边界条件u(h)=-v0代入式(9),可得在h2≤z≤h区间内, (10) 在区域C中,uC为常数,且u(h1)=u(h2),则有 (11) 由式(8)-(11)可得,Ⅰ、C及Ⅱ各区域的流速u(z)为 (12) MRF体积流量 (13) 在阀式流动模式中,压强梯度 (14) 由于总阻尼力Fd=ΔpAp,其中Ap为活塞截面积,则联立式(12)-(14)可得 Fd=Fη+Fτ, (15) 式中: 为黏滞阻尼力; Fτ=τycApL/h, 为可调阻尼力,其中c=2.07+1/[1+0.4wh2τy/(12ηQ)],为调整系数。 可调系数ε为总阻尼力Fd与黏滞阻尼力Fη之比,即 (16) 由式(15)可知:Fd主要由Fη和Fτ两部分组成;当MRD几何尺寸及MRF性质确定后,结合式(13)可知,Fη的大小仅受v0的影响;Fτ则是与τy相关的函数,其受磁场强度的影响,因此可通过改变加载在线圈上的电流I调节Fτ,实现变阻尼。 为实现对MRD的控制,按照QC/T545—1999《汽车筒式减振器台架试验方法》[12]测试MRD的阻尼特性和力学特性。采用正弦激励,振幅为±25 mm,分别测试阻尼力-位移和阻尼力-速度特性,其中v0=0.1,0.2,0.3,0.4,0.5 m/s,I=0,0.25,0.5,0.75,1,1.5,2 A。限于篇幅,只提供v0=0.1 m/s时的阻尼力-位移特性曲线,如图6(a)所示,而阻尼力-速度和阻尼力-电流特性曲线分别如图6(b)、(c)所示。 由图6(a)可知:阻尼力-位移示功曲线饱满,说明浮动活塞式体积补偿装置可有效补偿活塞杆拉伸和压缩时产生的体积差;阻尼力随加载电流的增大而增大,且示功曲线所包围的面积也随之增大,表明MRD的耗功能力在不断增加。 由图6(b)可知:当加载电流相同时,阻尼力随速度的增大呈线性增加趋势,这部分阻尼力主要由黏滞阻尼力产生;当速度一定时,阻尼力随加载电流的增大而增大,这部分由可调阻尼力提供,与Bingham模型变化特性相符;当v0=0.5 m/s时I=0 A,Fη=270.25 N,而I=2 A时Fd=743 N,根据式(16)可知ε=2.75,可调系数满足MRD对变阻尼的需求。 由图6(c)可知:阻尼力随加载电流的增大而增大,且增大速率先大后小。分析其原因为:在起初磁回路并未饱和的状态下,阻尼力的增大速率较大;而I>1 A时,随着磁回路逐渐饱和,阻尼力的增大速率变小。这与图3所示的MRF剪切屈服应力与磁感应强度关系的变化趋势相一致。 利用MATLAB中cftool函数拟合工具箱对MRD试验所得参数进行拟合。多项式拟合阶数越高,精度越高,同时越容易在曲线两端出现剧烈的Rouge振荡现象,因此取多项式拟合阶数为3阶。阻尼力Fd与I(0~2 A)和v0(-0.5~0.5 m/s)的关系式为 (17) 为了检验拟合得到的MRD模型的准确性,笔者提出利用最小二乘法对其进行校验。首先建立目标函数,使目标函数残差平方和最小,其表达式为 (18) 为了比较所建MRD力学模型与试验数据的拟合度,通过相对误差、相关系数和标准差3个指标对其进行校验。其中:相对误差可反映建立模型各个数据点与试验数据对应点的误差;相关系数则可反映建立模型与试验数据的相关性,相关系数越大,则二者相关性越好,建立的模型越准确;标准差可反映数据集的离散程度。3个指标的表达式分别为: 1) 相对误差 (19) 式中:Fd_max和Fd_min分别为给定试验状态下阻尼力的最大值和最小值。 2)相关系数 (20) 3) 标准差 限于篇幅,在此给出正速度下3个指标的统计结果,如图7所示。 由图7(a)可知:除I=0.25 A和v0=0.5 m/s时阻尼力-速度的最大相对误差为10.62%以外,其余的相对误差大都小于5%,说明相对误差较小。由图7(b)可知:相关系数随速度的增大先增大后减小,但均在0.995以上,说明拟合函数与试验数据线性相关度较好。由图7(c)可知:标准差值随速度的增大而增大,说明速度越大,数据集越离散,表明MRD在速度较大时的工作稳定性较差,应尽量使MRD工作在|v0|<0.3 m/s的低速条件下。 拟合得到的阻尼力-速度和阻尼力-电流特性曲线如图8所示,可见:与图6(b)、(c)的拟合度较好,表明建立的MRD力学模型较准确。 天棚ON-OFF半主动控制算法是美国学者KARNOPP等[13]于1974年最早提出的,该算法实现较为简单,对车辆低频振动有较好的控制效果,且得到了广泛应用。该算法的表达式为 (22) 该型军用轮式越野车为独立悬挂,假设其车身质量分配系数为1,则可用1/4车二自由度模型描述车辆悬挂动力学模型。基本假设为:1) 每个车轮的路面输入相同;2) 车身为刚体,无形变;3) 车轮视为无阻尼元件,仅有刚度;4) 悬挂系统视为弹性元件和阻尼元件的组合。基于上述假设,装有MRD的1/4车悬挂动力学模型如图9所示。 根据牛顿第二定律,悬挂运动微分方程为 (23) 1/4车悬挂动力学参数如表1所示。表中:cp为原被动阻尼系数;[fd]为悬挂许用行程。 表1 1/4车悬挂动力学参数 基于路面谱激励试验台搭建MRD振动控制试验系统。其中:车身垂直加速度传感器和悬挂相对位移传感器用了采集车辆状态信息;数据采集、控制及MRD电流驱动集成模块组将数据采集板卡、控制板卡和MRD电流驱动板卡集成,兼具数据采集、控制及MRD供电的功能;控制上位机用于控制集成模块组;供电电源为各个模块和部件供电;路面谱激励试验台控制上位机用于对液压激振台进行控制。采用谐波叠加法生成随机路面谱[14],并将其导入路面谱激励试验台控制系统中,液压激振头按照导入的随机路谱振动而模拟随机路面。MRD振动控制试验系统框图及实物图分别如图10、11所示。 3.2.1 时域分析 取D级随机路面10 m/s车速作为激励条件,图12为随机激励响应时域图,随机激励响应指标统计结果如表2所示。可以看出:相比于被动悬挂,天棚ON-OFF半主动控制可使车身垂直加速度均方根值降低10.63%,悬挂动行程均方根值恶化31.37%,但未超过[fd]/3=0.04 m。分析其原因为:由天棚ON-OFF半主动控制的传递特性可知,其有效的控制频段主要是车身共振区附近的低频段,而其余频段的控制失效甚至恶化;在覆盖的所关心的主要频段[0.1,25] Hz内,各指标均方根值统计结果是一个均方值,故对乘坐舒适性的改善有限。 控制方式车身垂直加速度/(m·s-2)悬挂动行程/m被动悬挂1.042 50.010 2天棚ON-OFF0.931 70.013 4变化率/%10.63-31.37 3.2.2 频域分析 图13为随机路面频域图。可以看出:在天棚ON-OFF半主动控制条件下,对车身垂直加速度的衰减主要集中在车身共振区附近的低频区域,其余频段的控制失效;而对悬挂动行程的恶化集中在中、低频段,车身共振区附近恶化最明显。为提高天棚ON-OFF半主动控制效果,在随机路面条件下,应在悬挂振动频段位于车身共振的低频附近时进行控制,此时ON-OFF控制效果较好。 1) 当MRD结构一定时,MRD阻尼力主要受MRF剪切屈服应力和磁场强度间相互关系的影响。MRD特性试验结果表明:阻尼力随v0的增大呈线性增大趋势,与Bingham模型相符;阻尼力随I增大而增大的变化趋势先快后慢,其中I<1 A时,阻尼力随I的增加而增长较快,I>1 A以后磁回路基本达到磁饱和,与MRF性质一致。 2) 利用最小二乘法对拟合得到的MRD多项式力学模型进行校验,结果表明:相关系数、相对误差及标准差均较小,说明该MRD力学模型可较准确地描述MRD力学性能;标准差随着v0的增大而增大,说明数据集越来越离散,表明MRD在v0较大时的工作稳定性较差,应尽量使MRD工作于|v0|<0.3 m/s的低速条件下。 3) 天棚ON-OFF半主动控制可使车身垂直加速度均方根值降低10.63%,在车身共振区低频段控制效果较好,而在其余频段的控制基本失效。军用越野车辆行驶路况较恶劣,工作频段较低,而该控制算法简单实用,可降低系统时滞,起到有效的控制效果,具有较好的实用价值。 参考文献: [1] 周长城.车辆悬架设计及理论[M].北京:北京大学出版社,2011:45-55. [2] 金耀,于德介,陈中祥,等.内分泌LQR控制策略及其主动悬架减振研究[J].振动与冲击,2016,35(10):49-54. [3] HEMANTH K,KUMARL H,GANGADHARANL K V.Vertical dynamic analysis of a quarter car suspension system with MR damper[J].Journal of the brazilian society of mechanical sciences and engineering,2017(39):41-51. [4] 欧进萍.结构振动控制:主动、半主动和智能控制[M].北京:科学出版社,2003:56-67. [5] BOADA M J L,CALVO J A,BOADA B L,et al.Modeling of a magneto-rheological damper by recursive lazy learning[J].International journal of non-linear mechanics, 2011(46):479-485. [6] 金京设,陈照波,程明,等.改进阻尼特性的内置平行双线圈磁流变阻尼器研究[J].农业机械学报,2017,48(3):368-375. [7] 陈士安,祖广浩,姚明,等.磁流变半主动悬架的泰勒级数LQG时滞补偿控制方法[J].振动与冲击,2017,36(8):190-196. [8] KHAN I U,DAVID W,NEIL D S.Improving the vibration suppression capabilities of a magneto-rheological damper using hybrid active and semi-active control[J].Smart mater struct,2016(25):1-15. [9] 陈昭晖,倪一清.磁流变阻尼器非参数化模型泛化能力的提高[J].振动与冲击,2017,36(6):146-151. [10] BITARAF M,OSMAN E O,STEFAN H,et al.Application of semi-active control strategies for seismic protection of buildings with MR dampers[J].Engineering structures,2010(32):3040-3047. [11] 关新春,郭鹏飞,欧进萍.基于有限元动网格技术的磁流变阻尼器瞬态阻尼力的数值计算[J].工程力学,2010,27(12): 46-58. [12] 国家机械工业局.汽车筒式减振器台架试验方法:QC/T545—1999[S].北京:中华人民共和国汽车行业标准,1999:506-510. [13] KARNOPP D,CROSBY M J,HARWOOD R A.Vibration control using semi-active force generators[J].ASME journal of engineering for industry,1974,5(2): 619-629. [14] 常志权,罗虹,褚志刚,等.谐波叠加路面输入模型的建立及数字模拟[J].重庆大学学报(自然科学版),2004,27(12):5-8.1.3 MRD特性试验
2 MRD力学模型及校验
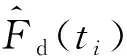
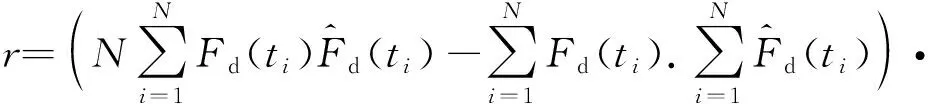
3 MRD天棚ON-OFF半主动控制
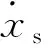
3.1 1/4车悬挂动力学模型


3.2 振动控制试验
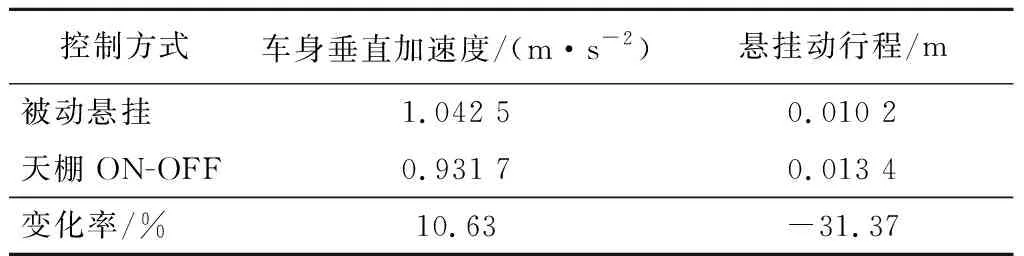
4 结论
