反积型信息熵及其在图像分割中的应用

王 帅, 李 婷, 于永利

(1. 陆军工程大学石家庄校区信息工程系， 河北 石家庄 050003；2. 陆军工程大学石家庄校区装备指挥与管理系， 河北 石家庄 050003)

熵的概念源自于热力学，是表征物质状态的参量，其物理意义是体系混乱程度的度量[1]。香农于1948年提出信息熵的概念，并给出了数学表达，解决了信息度量问题[2]。信息熵出现后，在诸多领域得到了广泛应用。图像分割作为计算机图形图像处理中的基础技术，是读取、分析和理解图像信息的关键步骤。1980年以后，国内外众多研究者将熵的概念应用于图像分割处理，并进行了大量研究。如：曹建农[3]系统地阐述了信息熵、Renyi熵、Tsallis熵等新型熵在图像分割处理中的应用，并基于此对比了全局熵、局部熵、指数熵、高维熵、条件熵、联合熵和交叉熵等基本熵，同时对比了一维熵和二维熵的应用；吴成茂[4]研究了新型信息熵及其性质，并用于图像分割，获得了良好效果；林佳颖[5]和冉清华[6]研究了基于Renyi熵图像分割算法；盛春冬[7]和唐土生等[8]研究了模糊熵在图像分割中的应用；张新明等[9]研究了基于Tsallis熵采用广义概率进行图像分割；路亚缇[10]将粒子群优化算法应用于最大熵多阈值图像分割方法中；陈恺[11]将萤火虫算法和二维熵多阈值方法结合起来进行快速图像分割；张晓丽[12]研究了基于改进差分进化算法进行二维最大熵图像分割；李爱菊等[13]采用改进布鸟算法进行最大熵值图像分割等。上述研究均在一定程度上提高了图像分割效果，丰富了图像分割内涵，但也有一定的适用范围。为简化图像分割算法，提高图像分割处理效率，笔者在信息熵的基础上定义一种反积型信息熵，并证明其性质，最后通过采用二维阈值最大熵值法并结合图像分割实例应用验证该熵的有效性和实用性。

1 信息熵

(1)

信息熵的典型性质为[2-3]：

1) 非负性。对于任意离散概率分布P，则有0≤H(P)≤logn。

2) 确定性。对于任意离散概率分布P，当P=(0,0,…,0,1,0,…,0)时，则有H(P)=0，即离散事件中，如果有确定性的事件发生，那么其信息熵为0。

3) 对称性。当p1,p2,…,pn的顺序任意互换时，H(P)值不变。

4) 可加性。独立事件的熵等于各独立事件的熵之和，即H(PQ)=H(P)+H(Q)。

信息熵在描述信息不确定度时，对于一个n状态系统，pi作为第i个事件发生的概率，则第i个事件的信息量可表示为

H(pi)=-pilogpi。

(2)

由式(2)可推出：pi越大，其信息量越小，即第i个事件的不确定度越小。因此，本文提出反积型信息熵，用于描述n状态系统的信息量。

2 反积型信息熵

2.1 定义

对于第i个事件，其发生的概率为pi，那么其信息量表征为1-pi。对于离散概率分布P=(p1,p2,…,pn)，n状态系统的熵值H′(P)命名为反积型信息熵，可表示为

(3)

反积型信息熵的含义为：离散系统的信息量，可使用离散事件中原发生概率取反后的相互乘积来衡量。反积型信息熵具有如下性质：

2) 确定性。对于任意离散概率分布P，当且仅当P=(0,0,…,0,1,0,…,0)时，有H′(P)=0，即离散事件中，如果有确定性的事件发生，那么其信息熵为0。

4) 不可加性。独立事件的熵不等于各独立事件熵之和，即H(PQ)≠H(P)+H(Q)。

反积型信息熵的不可加性是显而易见的，这里不作证明，而仅证明性质1)-3)。

2.2 证明

2.2.1 非负性证明

因为

0≤pi≤1，

则

进而

因为

所以

2.2.2 确定性证明

对于任意离散概率分布P，当P=(0,0,…,0,1,0,…,0)时，1-P=(1,1,…,1,0,1,…,1)，因此

且上述离散事件顺序可任意调换。

由于

并且

所以

(4)

又因为

0≤pi≤1，

所以

2.2.3 对称性证明

由性质1)证明可知

当且仅当1-p1=1-p2=…=1-pn时等号成立，

也即

则有

3 信息熵在图像分割中的应用

3.1 二维阈值最大熵值法图像分割原理

阈值分割法是图像分割中基本而又广泛使用的一种方法，其思想是采用阈值来划分图像中的目标物与其背景物灰度，使目标从背景中分离出来。阈值分割方法的原理为：设原始灰度图像函数为f(x,y)，以一定的准则在f(x,y)中找出一个灰度值t作为阈值，将图像分割为2部分，分割后的二值函数

(5)

二维阈值化图像分割方法则需要同时考虑像素点的灰度值及其邻域平均灰度值,其原理为：将f(x,y)看作一个二维灰度图像函数，其邻域灰度值为g(x,y)，设二维分割阈值分别为s和t，则对图像函数f(x,y)以二维阈值分割后的二值函数记为fs,t(x,y)，即

(6)

假定有一幅数字灰度图像G，表示为G=[g(x,y)]M×N(1≤x≤M，1≤y≤N)，则该图像中灰度的变化为0～L-1(L=256)，对于图像上任何一个像素点m×n(m、n通常取值为3)，有像素灰度值u和邻域平均灰度值v与其对应。设ruv表示图像G中像素灰度值为u，且其邻域平均灰度值为v的像素点的个数，有

(7)

则定义二元组(u,v)在图像G中的二维联合概率密度p(u,v)，则有[4,14]

(8)

式(8)本质上是一个二维均值直方图，相比较一维阈值图像分割，其用于图像分割能够降低图像噪声和边缘的影响，可较好地保证图像分割效果，但二维均值表示复杂，计算量大，必然增加计算时间。本文将分别使用信息熵最大熵值法和反积型信息熵最大熵值法求解二维阈值，再利用所得二维阈值进行典型图像分割，对比图像分割效果以及所耗时间。

提取原始图像任意像素点的灰度值以及计算该像素点邻域平均灰度值之后，根据给定的二维阈值(s,t)，将图像二维联合概率密度分割成A、B、C、D四个典型区域。一般而言，图像中目标点和背景点在图像像素中所占比例最大，且目标区域和背景区域内部的像素点灰度级比较均匀，点灰度及其区域灰度均值相差不大，导致目标点和背景点往往集中在对角线附近[14]。因此，可用对角线连接图1中的A、B区域，使其分别对应于目标和背景，而将远离对角线的C、D区域分别对应噪声和边缘。图像二维阈值分割分区表达如图1所示。

此时，假设目标概率和背景分别为CA和CB，其出现的概率分别为

(9)

则目标CA的灰度级(u,v)所对应的概率分布为

(10)

同样地，背景CB的灰度级(u,v)所对应的概率分布为

(11)

根据基于信息熵的二维直方图阈值化分割准则，可得二维最优阈值(sopt,topt)为

H(s,t,CB)}，

(12)

式中：

(13)

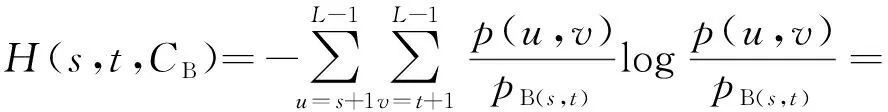
(14)

分别为给定阈值(sopt,topt)分割图像所得目标CA和CB的信息熵。

相应地，反积型信息熵分别为

(15)

(16)

3.2 二维阈值图像分割过程

为了验证反积型信息熵的有效性，分别采用信息熵二维最大阈值分割法和反积型信息熵二维最大阈值分割法对图像进行分割实验，具体图像分割处理流程如图2所示。其中：选用的图像处理工具是MATLAB2011b，计算机配置为Intel(R) CoreTMi7-6700 @2600 GHz，8 GB内存，64_位Windows7操作系统。

限于篇幅，选用了5幅典型灰度图像作为示例说明，采用2种二维阈值法对其进行分割，其图像及其分割效果如图3-7所示，表1为5幅图像对应的阈值和时间消耗。

由图3-7可以看出：反积型信息熵用于二维阈值图像分割是可行的。同时，由图4、5、7可以清晰地看出：在图像分割细节方面，反积型信息熵的分割效果优于信息熵分割效果，进一步验证了反积型熵的有效性。反积型信息熵的数学性质有效支撑了其在图像分割领域的可行性和有效性，说明了其与信息熵在进行信息量量化方面本质上是一致的。

图像名称原图大小/kB信息熵分割法反积型信息熵分割法阈值计算时间/s阈值计算时间/sLena512×512 258(123,120)32.132 4(112,99)11.510 2手骨骼307×409 124(32,29)10.169 7 (41,35)4.538 3文本320×240 77 (168,166)18.067 8(167,162)7.532 3楼梯254×252 65 (115,121)12.170 5(115,109)4.684 1小兔461×461 210(121,80)21.106 0(99,115)11.167 9

由表1可以看出：反积型信息熵的计算时间远小于信息熵计算时间，后者约为前者的2.5倍，与理论结论相符。

4 结论

本文提出了反积型信息熵，并从数学性质和图像分割应用2个角度证明了该熵的有效性，且该信息熵表达简单，便于理解，同时实验结果表明其能够大幅减少计算时间，进一步丰富了信息熵的理论，具有一定的现实意义。但在进行计算时并未对求解过程进行优化，若与其他优化算法结合使用，则能够进一步节省图像分割时间，提高分割效率。

参考文献：

[1] 傅祖芸.信息论-基础理论与应用[M].3版.北京:电子工业出版社,2011:1-40.

[2] 高秀峰,齐剑锋.军事信息技术基础[M].北京:电子工业出版社,2017:5-20.

[3] 曹建农.图像分割的熵方法综述[J].模式识别与人工智能,2012,25(6):958-969.

[4] 吴成茂.一种新信息熵定义及其在图像分割中的应用[J].西安邮电学报,2009,14(1):72-78.

[5] 林佳颖.基于Renyi熵的图像分割算法研究[D].长春:吉林大学,2010:10-13.

[6] 冉清华.基于Renyi熵理论的图像分割算法研究[D].重庆:重庆大学,2011:13-23.

[7] 盛春冬.基于变精度粗糙熵的职能图像分割方法研究[D].哈尔滨:哈尔滨工程大学,2011:17-28.

[8] 唐土生,陈绚青.基于超模糊熵ULPCNN二值图像分割算法研究与实现[J].激光杂志,2016,37(1):113-116.

[9] 张新明,张贝,涂强.广义概率Tsallis熵的快速多阈值图像分割[J].数学采集与处理,2013,31(3):502-511.

[10] 路亚缇.基于粒子群优化算法的最大熵多阈值图像分割研究[D].郑州:郑州大学,2015:13-22.

[11] 陈恺.基于萤火虫算法的二维熵多阈值快速图像分割[J].光学精密工程,2014,22(2):517-523.

[12] 张晓丽.基于改进差分进化算法的二维最大熵图像分割[J].自动化技术与应用,2016,35(6):71-76.

[13] 李爱菊,钮文良,王廷梅.改进布鸟搜索算法最大熵值的医学图像分割[J].计算机仿真,2014,31(8):421-425.

[14] 张毅军,吴雪菁,夏良正.二维熵图像阈值分割的快速递推算法[J].模式识别与人工智能,1997,10(3):259-263.