基于OFDM的合成孔径雷达距离模糊抑制

李小萍

(中国电子科技集团公司第三十八研究所，安徽 合肥 230088)

0 引 言

合成孔径雷达(SAR)具有全天时、全天候成像的优异性能，是遥感探测的重要途径。通过信号处理，SAR可以获得高分辨率图像，但是由于最小天线面积的限制，SAR不得不在距离模糊和方位向分辨率之间进行折衷[1-2]。对于广域监视，尤其是对于星载SAR系统，距离模糊是其面临的关键问题。

在SAR中，如果当前发射脉冲的回波是在后续脉冲已经发射后接收到，那么，所接收到的信号就会存在距离模糊问题。如图1所示，无距离模糊区域的散射回波将会被距离模糊区域的散射回波遮挡。在进行方位压缩时，将会造成模糊区域的散焦和错译，为了解决该问题，学者们已经提出了多种解决方法[3-10]。

图1 SAR成像场景

虽然可以通过降低脉冲重复频率(PRF)的方式解决距离模糊问题，但是，这样会造成方位向分辨率的下降，且易导致多普勒模糊[3]。为了在不降低PRF的情况下，解决距离模糊问题，已有学者提出了解决方法[4-10]。例如，文献[4]提出了上下调频波形，用于区分无距离模糊区和距离模糊区的回波信号，该方法可以解决存在一次距离模糊的情况，但对于多次距离模糊问题，该方法已不再适用。文献[5]提出了方位向编码的方法，该方法通过对方位向进行编码，将不同的距离模糊搬移到不同的多普勒谱上，通过方位向滤波消除距离模糊。文献[6]提出了块编码技术，通过匹配滤波的方式抑制距离模糊。文献[7]将正交频分复用(OFDM)和线性调频(LFM)波形相结合，提出了减轻距离模糊问题的方法。此外，为了抑制距离模糊，文献[8]～[10]提出了编码OFDM波形，但是该方法只能解决临近距离的模糊问题，且临近2次发射波形的正交性较差，同时存在距离分辨率下降的问题。

为了抑制距离模糊，同时确保距离分辨率没有损失，本文提出了随机相位编码OFDM波形，通过对不同发射脉冲进行独立相位编码，可以有效抑制不同的距离模糊。

1 问题描述和建模

1.1 OFDM信号模型

第p个脉冲发射的OFDM信号可以表示为：

(1)

式中：NU=⎣(Nc-1)/2」，NL=⎣Nc/2」，Nc为子载波个数，⎣·」表示下取整；am,p为第m个子载波和第p个脉冲上所调制的编码，下文将对其设计问题进行讨论；Δf为子载波间隔；T为每个基本OFDM符号的持续时间，且T=1/Δf；Tr为脉冲重复间隔；rect[t/T]为矩形窗函数，当0≤t≤T时其值为1，其他情况下为0。

可以看出，整个发射信号的带宽为B=NcΔf。

1.2 距离模糊抑制原理

在实际中，如果雷达接收到的回波信号是由不同发射脉冲的回波信号构成，那么就会存在距离模糊问题。而之所以存在距离模糊问题，是由于雷达接收机无法区分不同发射脉冲的回波信号。如果雷达接收机可以区分不同发射脉冲的信号，那么距离模糊问题就会迎刃而解。

对于SAR系统而言，采用脉冲压缩(即匹配滤波)的方式，提高距离分辨率和输出信噪比(SNR)。如果不同脉冲发射的信号是正交的，那么，雷达接收信号经过1组匹配滤波器后，就可以区分不同发射脉冲的回波信号，从而解决距离模糊问题。本文基于此思想，通过对所发射的OFDM信号进行设计，以达到解决SAR中距离模糊的问题。

不同发射脉冲的正交特性可以表示为：

(2)

式中：(·)*表示共轭运算；δ(p-p′)为 Dirac delta函数。

那么，匹配滤波器的输出可以表示为：

(3)

式中：yp(t)为第p个发射脉冲的匹配滤波器输出；x(t)为接收信号；∘表示卷积运算。

不失一般性，如果忽略噪声干扰和信号的幅度衰落，接收信号可以看作是发射信号经过不同时延和多普勒调制后的叠加结果；因此，可以利用不同发射信号的互模糊函数来评估对距离模糊的抑制性能。

第p个发射脉冲和第p′个发射信号的互模糊函数可以表示为：

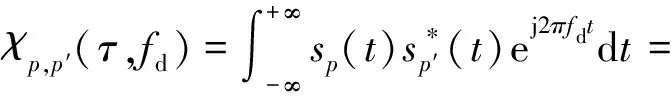
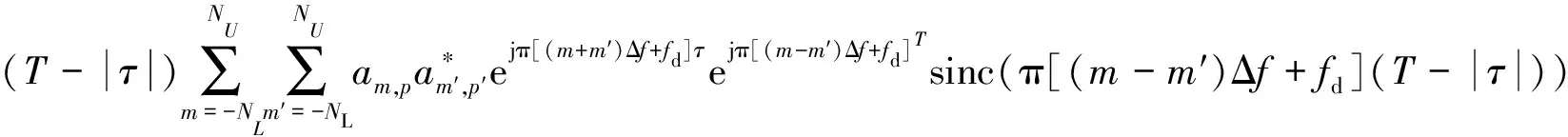
(4)

式中：τ为时间延迟；fd为多普勒频移；sinc(x)=sinx/x，x表示对x取绝对值。

可以看出，当p=p′时，式(4)中的互模糊函数将表示sp(t)的模糊函数，当am,p∈{0,1}，式(4)将与文献[10]中的互模糊函数相一致。

2 OFDM波形设计

本节将提出OFDM波形设计方法，理想情况下，当p≠p′时，如果式(4)的互模糊函数为0，那么距离模糊问题就可以得到解决。

理论上，如果编码am,p的相位是独立均匀分布的，那么，可以得到下面的结果[11]：

(5)

式中：E[·]表示求期望。

由式(5)可知，式(4)的期望可以表示为：

Eχp,p′(τ,fd)=

(6)

如果子载波的数目足够大，那么χp,p′(τ,fd)将会趋近于它的期望值。

根据文献[12]中星载SAR系统的参数：脉冲持续时间为40 μs，信号带宽为20 MHz，如果要达到相同的系统性能，那么，OFDM信号的子载波数要达到800。此外，如果SAR系统可以满足脉冲持续时间增长或者系统带宽增大的条件，可以使OFDM信号的子载波数目得到进一步提高。此外，通过对不同发射脉冲信号进行随机相位编码，从而使所设计的OFDM信号的互模糊函数更加接近式(6)的结果，以达到抑制距离模糊的目的。

实际中，通过对不同的发射脉冲调制独立的随机相位编码，并经过1组匹配滤波器，从而达到抑制距离模糊的目的。图2给出了无距离模糊宽幅成像的具体实现流程。接收信号经过1组匹配滤波器后，每一路输出为距离模糊抑制后的1条子带，再经过方位向处理，就可得到不同子带的像，最后，将这些子带的像沿着距离维拼接，就可得到无距离模糊的宽幅像。

图2 无距离模糊宽幅成像流程

3 仿真分析

本节将通过实验仿真分析验证所提方法的有效性。仿真中，信号带宽为20 MHz，脉冲持续时间为40 μs。此外，在仿真实验中，分别与文献[4]和[10]中所设计的波形的性能进行对比，其中，文献[4]和[10]中的结论分别表示为“UD-LFM”和“C-OFDM”，所提方法表示为“R-OFDM”。

为了评估所设计的波形的性能，本文采用成像中的某些性能指标进行描述，包括峰值旁瓣比(PSLR)、积分旁瓣比(ISLR)、最大相对互模糊函数(MRCA)和距离分辨率。

根据文献[12]，PSLR定义如下：

(7)

式中：Ps为最大旁瓣功率；Pm为最大主瓣功率。

积分旁瓣比(ISLR)定义为：

(8)

式中：Es为旁瓣能量；Em为主瓣能量，本文中主瓣为第1对零点之间的区域。

最大相对互模糊(MRCA)函数定义为：

(9)

可以看出，MRCA越小，对距离模糊的抑制性能也就越好，因此，在波形设计中，MRCA应尽可能地小。

表1给出了不同波形在不同性能参数下的比较结果，对比表1中的结果可以看出，由于C-OFDM波形失去了频谱两端的子载波，因此，C-OFDM波形的距离分辨率均存在损失，而所设计的R-OFDM和UD-OFDM波形具有更高的距离分辨率。R-OFDM和UD-OFDM波形具有优异的PSLR性能，而C-OFDM波形的PSLR性能最差，这是由于C-OFDM波形在频谱上不连续，存在频谱间隙。所设计的波形R-OFDM的ISLR性能要比C-OFDM波形好，但与UD-LFM波形相比较差。

此外，与其他波形相比，所设计的波形R-OFDM具有最好的MRCA特性，也就是说，所设计的波形R-OFDM具有最好的正交特性，这对于距离模糊抑制尤为重要。本文所提方法通过采用随机相位编码进行调制，可以设计出多个相互正交的波形，而传统的设计方法(如C-OFDM和UD-OFDM波形)只能设计出1对正交的波形，从而导致这些波形只能抑制有限的距离模糊。

表 1 不同波形的性能指标

图3给出了所设计的波形的模糊函数。从图中可以看出，所设计的波形的模糊函数具有图钉状特性，即具有尖锐的峰和类似于噪声的旁瓣。图4(a)给出了不同波形的互模糊函数时延维的特性，图4(b)给出了不同波形互模糊函数多普勒维的特性。无论是对于互模糊函数的时延维还是多普勒维，所设计的波形R-OFDM的性能最好。C-OFDM波形的互模糊函数的时延维特性要优于UD-LFM波形，但其互模糊函数的多普勒维特性较差。上述仿真实验同时也说明所设计的波形R-OFDM具有优异的互模糊函数特性，也就是说，其具有优异的距离模糊抑制性能。

图3 所设计波形的模糊函数

图4 互模糊函数特性

4 结束语

为了解决SAR成像中距离模糊问题，本文提出了随机相位编码OFDM波形设计方法。通过简单的匹配滤波处理，就可以对距离模糊达到有效的抑制，而且所设计的波形具有图钉状的模糊函数特性，也不存在距离分辨率下降的问题。此外，与其他传统的波形相比，本文所提方法设计的波形具有较好的PSLR和ISLR特性，以及优异的MRCA特性。

[1] CURLANDER J C,MCDONOUGH R N.Synthetic Aperture Radar:Systems and Signal Processing[M].New York:Wiley,1991.

[2] LI F,JOHNSON W T K.Ambiguities in spaceborne synthetic aperture radar systems[J].IEEE Transactions on Aerospace and Electronic Systems,1983,AES-19(3):389-397.

[3] FREEMAN A.On ambiguities in SAR design[C]//Proc.6th Eur.Conf.Synthetic Aperture Radar,2006：1-4.

[4] MITTERMAYER J,MARTNEZ J M.Analysis of range ambiguity suppression in SAR by up and down chirp modulation for point and distributed targets[C]//2003 IEEE International Geoscience and Remote Sensing Symposium,2003：4077-4079.

[5] DALL J,KUSK A.Azimuth phase coding for range ambiguity suppression in SAR[C]//2004 IEEE International Geoscience and Remote Sensing Symposium,2004:1734-1737.

[6] AKHTAR J.Cancellation of range ambiguities with block coding techniques[C]//2009 IEEE Radar Conference,2009:1-6.

[7] WANG W Q.Mitigating range ambiguities in high-PRF SAR with OFDM waveform diversity[J].IEEE Geoscience and Remote Sensing Letters,2013,10(1):101-105.

[8] RICHÉ V,MÉRIC S,POTTIER É,BAUDAIS J.OFDM signal design for range ambiguity suppression in SAR configuration[C]//2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS),2012:2156-2159.

[9] RICHÉé V l,MERIC S,BAUAIS J,POTTIER É.Optimization of OFDM SAR signals for range ambiguity suppression[C]//Proceedings of the 9th European Radar Conference,Amsterdam,the Netherlands,2012: 278-281.

[10] RICHÉ V,MÉRIC S,BAUDAIS J,POTTIER É.Investigations on OFDM signal for range ambiguity suppression in SAR configuration[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(7)：101-105.

[11] FIRAT TIGREK R,De HEIJ WIM J A,VAN GENDEREN P.OFDM signals as the radar waveform to solve Doppler ambiguity[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):130-143.

[12] CUMMING I G,WONG F H.Digital Processing of Synthetic Aperture Radar Data:Algorithms and Implementation[M].Boston,MA,USA:Artech House,2005.