大坝混凝土分数阶徐变模型探讨

，，， ， (.三峡大学 水利与环境学院，湖北 宜昌 44300； .中国电建集团 贵阳勘测设计研究院有限公司，贵阳 55008)

1 研究背景

徐变对混凝土的受力和变形性能有显著影响，在混凝土结构计算中不容忽视。徐变模型是反映徐变度或徐变变形随时间变化规律的数学函数式，徐变预测的有效性和准确性很大程度上取决于徐变模型的选取。

徐变模型一直是土木工程界研究的热点，在有足够多徐变试验资料的情况下，可用数学方法直接建立徐变与加载龄期及持荷时间的关系。常用的徐变表达式可分为2大类：一类是表示徐变与持荷时间的关系，如幂函数式、对数函数式、双曲线函数式等；另一类是表示徐变与加载龄期及持荷时间的关系，如幂指数函数式、多项式指数函数式。在缺乏足够多徐变资料的情况下，往往要通过经验公式来估算徐变值，常用的徐变估算方法有CEB/FIP方法、ACI方法、BAPⅡ方法、CS方法、以及朱伯芳提出的朱氏公式和成都勘测设计研究院提出的由弹性模量推算徐变的方法。上述徐变模型各有局限性及适用性[1-4]，各徐变模型在精度上也存在一定的差异[5-6]。

分数阶微积分是一个解决物理力学建模难题的有力工具。例如理想固体的应力-应变关系满足胡克(Hooke)定律，理想流体满足牛顿(Newton)定律，介于理想固体和理想流体之间的材料应满足σ(t)-dβε(t)/dtβ(0≤β≤1)的关系，它不仅包含了理想固体和理想液体，而且刻画了处于它们之间的其他材料。分数阶微积分流变模型的引入，仅仅需要少数几个参数就可以模拟出复杂的应力-应变关系，这是整数阶微积分流变模型难以比拟的。但是到目前为止，分数阶微积分主要应用于岩体蠕变、电磁学、神经网络、混沌系统[7-9]等方面，而将分数阶微积分运用于混凝土徐变模型的实例很少。因此，本文基于分数阶微积分理论建立了混凝土徐变模型，将该理论引入混凝土徐变分析。

2 混凝土分数阶徐变模型

2.1 软体元件

设有一种元件代表处于理想流体和固体之间某种状态的物体，该物体称为软体，该元件称为软体元件[10]，软体元件本构方程为

(1)

式中：σ(t)表示应力；t为时间；η为黏弹性系数。当β=1，该元件就是阻尼器元件，代表理想流体；当β=0，该元件变为弹簧元件，代表理想固体。当σ(t)为常数时，即应力不变的情况下，软体元件将描述流变行为的徐变，对式(1)两侧进行拉普拉斯变换及逆变换，同时利用卷积定理[11]，可得

(2)

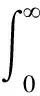
在应力不变的情况下，当β不同时，式(2)表示的是一系列的徐变曲线,即通过改变β，软体元件就能描述处于理想固体和理想液体之间的不同状态的流变行为。

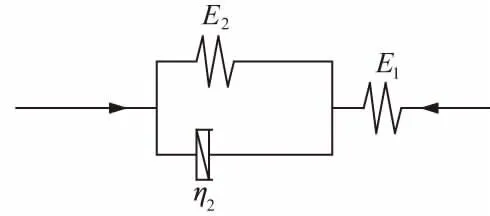
图1 带软体元件的广义开尔文模型Fig.1 Generalized Kelvin model with software component

2.2 带软体元件的广义开尔文模型

混凝土是由多种成分组成的复合材料，描述混凝土的徐变性能需要将不同的流变元件进行组合。本文通过带软体元件的广义开尔文模型对混凝土徐变性能进行分析，带软体元件的广义开尔文模型[11]见图1。

带软体元件的广义开尔文模型本构方程[11]为

(3)

式中D为分数阶微积分算子。

当σ(t)为常数时，由Riemann-Liouville型分数阶微积分算子理论，可得

2.3 分数阶徐变模型

朱伯芳[12]对比了广义开尔文模型与混凝土徐变柔量的狄利克雷(Dirichlet)级数之间的关系，认为目前混凝土工程上常用的8参数徐变模型是考虑了混凝土龄期的广义开尔文模型。此外，由于混凝土的徐变不仅与持荷时间有关，还与加载龄期有关。因此，当应力不变的情况下，根据Riemann-Liouville型分数阶微积分算子理论，结合式(4)和混凝土徐变特性，本文建立了考虑加载龄期的混凝土分数阶徐变模型的表达式为

C(t,τ)=(f1+g1τ-p1)·

(5)

式中：C(t,τ)为加荷龄期τ、持荷时间t-τ的徐变度；f1，g1，p1，r1，β均为待定系数，且0<β≤1。

当β=1时，得到徐变模型表达式为C(t,τ)=(f1+g1τ-p1)[1-e-r1(t-τ)]，该模型简化为考虑混凝土龄期的4参数模型。

3 算例分析

为验证分数阶徐变模型的准确性及方便与其他的徐变模型相比较，本文采用优化算法对建立的分数阶徐变模型、常用的8参数模型、4参数模型进行参数反演。模型参数反演是一个非线性规划中的数学问题，文献[12]对于参数反演的方法有详细介绍，本文不再重复列出。复合形算法[13]适合解决有约束条件的优化问题，而且计算结果较为可靠，故本文使用复合形法确定待定参数，并基于MatLab语言编写计算程序，然后结合各算例中的徐变度试验值对各徐变模型进行参数优选。

3.1 算例1

采取文献[12]中龚嘴重力坝基础部分混凝土的徐变试验资料，见表1。

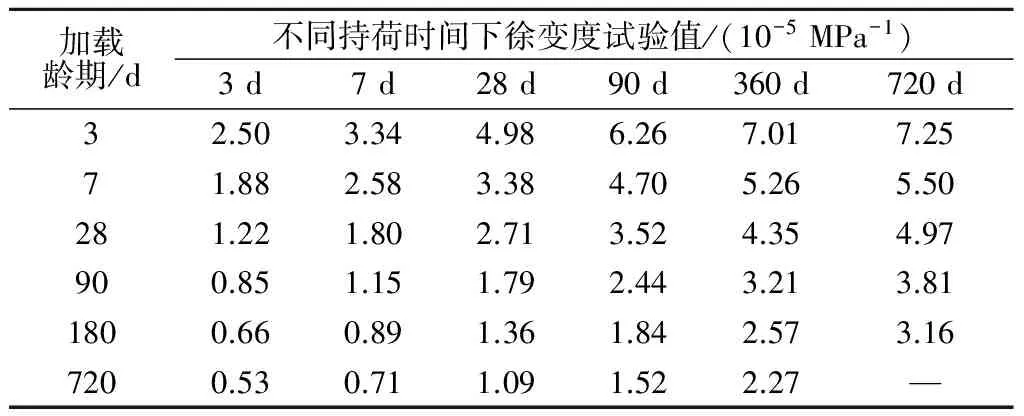
表1 龚嘴重力坝徐变度试验值Table 1 Creep test results of Gongzui gravity dam

注：加载龄期为720 d时持荷时间720 d的徐变数据缺失

针对龚嘴重力坝的混凝土徐变度试验值，对所建立的分数阶徐变模型、8参数模型、4参数模型进行参数反演。

对式(5)进行收敛性分析，当n>40时，分数阶模型表达式基本处于收敛。故本算例在编写MatLab程序时，取n=41。经过敏感性分析发现，f1，r1，β较其他2个参数敏感；通过对初始复合形法不断调试，优化得到模型参数见表2。

表2 分数阶模型参数反演结果Table 2 Results of parameter inversion of fractionalorder model

根据反演出的参数结果，确定出分数阶模型徐变度表达式为

C(t,τ)=(6.87+32.35τ-0.38)·

(6)

同理，反演出4参数模型徐变度表达式为

C(t,τ)=(1.54+7.81τ-0.39)[1-e0.078(t-τ)] 。

(7)

根据文献[12]可得8参数模型徐变度表达式及徐变度计算值。 图2给出龚嘴重力坝各加荷龄期的徐变试验值、分数阶模型计算值、8参数模型计算值、4参数模型计算值的徐变过程线对比。

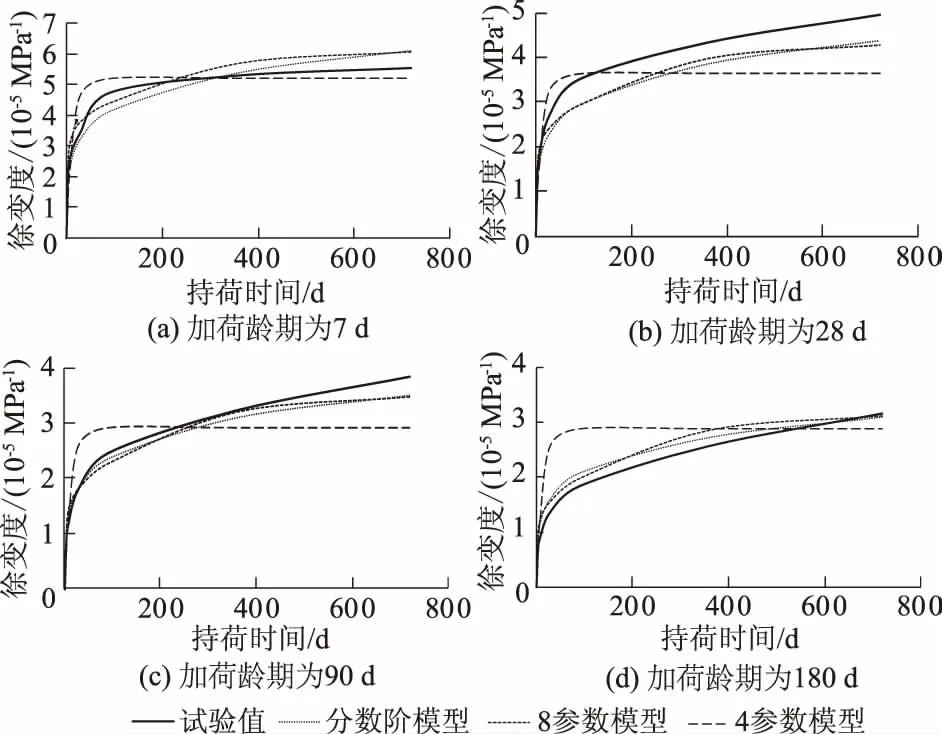
图2 龚嘴重力坝各加荷龄期的徐变过程对比Fig.2 Comparison of creep process of Gongzui gravity dam among different ages of loading

3.2 算例2

算例2采取文献[14]中锦屏工程混凝土的徐变试验资料，见表3。

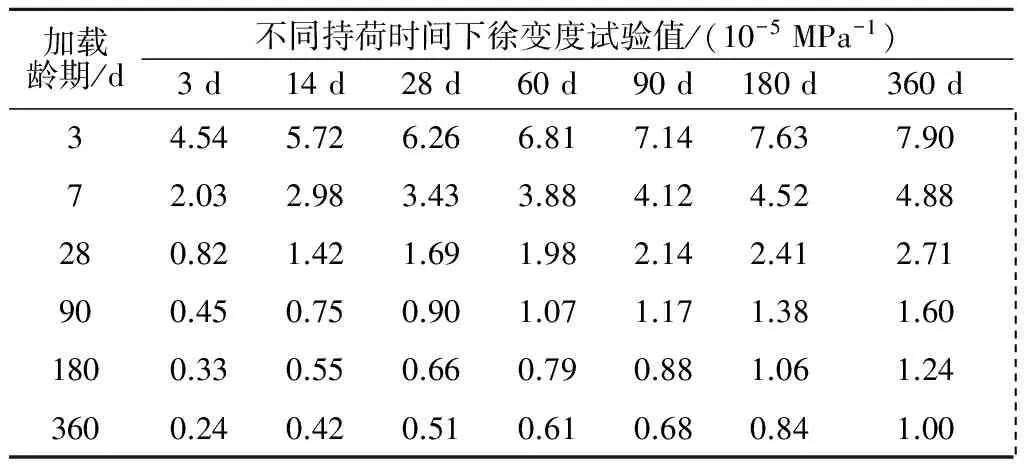
表3 锦屏工程徐变度试验值Table 3 Creep test results of Jinping arch dam

针对锦屏工程混凝土徐变试验值，对所建立的分数阶徐变模型、8参数模型及4参数模型进行参数反演。

对式(5)进行收敛性分析，本算例在编写MatLab程序时，取n=47,通过对初始复合形不断调试，优化得到分数阶模型参数。根据参数反演结果，得到分数阶模型徐变度表达式为

C(t,τ)=(0.17+20.66τ-0.53)·

(8)

同理，经参数反演得到8参数模型表达式为

C(t,τ)=(0.82+12.08τ-0.88)[1-e-0.406(t-τ)]+

(0.32+15.68τ-0.634)[1-e-0.001 5(t-τ)] 。

(9)

反演出4参数模型徐变度表达式为

C(t,τ)=(1.31+13.29τ-0.86)[1-e0.186(t-τ)] 。

(10)

图3给出锦屏工程混凝土各加荷龄期的徐变试验值、分数阶模型计算值、8参数模型计算值、4参数模型计算值的徐变过程线对比。

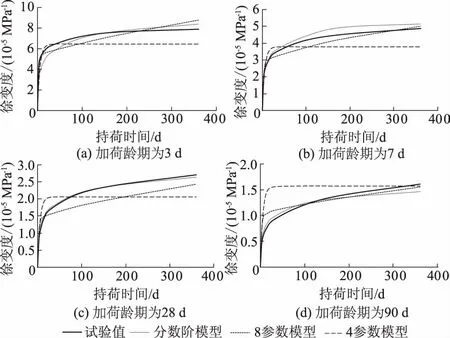
图3 锦屏工程各加荷龄期的徐变过程对比Fig.3 Comparison of creep process of Jinping arch dam among different ages of loading

分析图2、图3可知：

(1)对比分数阶模型、4参数模型,可以看出：当加载龄期<28 d时，分数阶模型、4参数模型均具有较高的拟合精度；而当加载龄期≥28 d时，分数阶模型较4参数模型的拟合效果要好，如4参数模型徐变度在持荷90 d后几乎不再增长，而分数阶模型可反映出混凝土徐变度随持荷时间增加而增长的趋势。

(2)对于图2来说,当加荷龄期较长时，分数阶模型拟合效果较8参数模型略好，如当加荷龄期为90 d时，分数阶模型与试验值的非线性相关系数为0.95，而8参数模型的非线性相关系数为0.93；加荷龄期较短时，8参数模型更优，如当加荷龄期为7 d时，分数阶模型与试验值的非线性相关系数为0.91，而8参数模型的非线性相关系数为0.92。对于图3来说,当加荷龄期为3，7 d时分数阶模型与8参数模型拟合效果较为接近，分数阶模型与试验值的非线性相关系数为0.90，8参数模型与试验值非线性相关系数为0.91；但在加荷龄期在28 d后，则分数阶拟合效果更优。

(3)总体上来说，分数阶模型拟合徐变度过程线和徐变度试验过程线吻合效果较好，拟合表达式的精度较高，如分数阶计算值与试验值最大比值为0.78，且各加荷龄期计算值与试验值的非线性相关系数均在0.9以上，这说明将分数阶模型运用于混凝土徐变预测中是行之有效的。

4 结 论

本文将分数阶微积分流变模型应用于混凝土的徐变研究中，给出了考虑加载龄期的混凝土分数阶徐变模型的表达式，并结合工程实例中土徐变度实测值优化反演模型参数。得到如下结论：

(1)结合龚嘴重力坝混凝土及锦屏工程混凝土徐变度试验值，基于混凝土分数阶微积分徐变模型，采用复合形法优化反演出徐变度表达式中的5个参数，采用此模型所得的徐变度计算值和试验值吻合效果较好。

(2)分数阶模型能较为准确地预测混凝土徐变，与8参数模型预测效果接近的同时，也克服了8参数模型所需要确定的参数较多的缺点，是一种良好的混凝土徐变预测模型。

参考文献：

[1] 黄国兴,惠荣炎,王秀军.混凝土徐变与收缩[M].北京：中国电力出版社，2011.

[2] NEVILLE A M, DILGER W H, BROOKS J J. Creep of Plan and Structural Concrete[M]. New York：Construction Press,1983.

[3] 潘钻峰,吕志涛,刘 钊,等.高强混凝土收缩徐变试验及预测模型研究[J].公路交通科技，2010，27(12)：10-15.

[4] 潘立本，张苏俊.混凝土收缩与徐变的实验研究[J].河海大学学报(自然科学版)，1997，25(5)：84-89.

[5] 曹国辉，胡佳星,张 锴，等.混凝土徐变预测模型修正分析[J].建筑结构，2014，(4)：45-49.

[6] 朱伯芳.关于混凝土徐变理论的几个问题[J].水利学报,1982,29(3):35-40.

[7] 陈家瑞,浦 海，肖 成，等.基于分数阶理论的破碎泥岩流变模型试验研究[J].中国矿业大学学报，2015,44(6): 996-1001.

[8] 张 昊，缪仲翠，张永义，等.基于分数阶PI～λ控制器的永磁同步电动机调速系统研究[J].电气应用，2015，(23):50-54.

[9] 潘晓明，杨绪君，李传东.时滞分数阶神经网络的稳定性分析[J].西南大学学报(自然科学版)，2016,38(5): 168-173.

[10] 黄耀英，郑 宏.整数及分数阶流变模型研究及应用[M].北京：中国水利水电出版社，2016.

[11] 黄耀英，郑 宏.分数阶微积分流变模型在岩体结构加速流变破坏分析中的应用[J].计算机辅助工程，2010，19(4):20-24.

[12] 朱伯芳. 大体积混凝土温度应力与温度控制[M].北京：中国电力出版社，1999.

[13] 龚 纯，王正琳. 精通MATLAB最优化计算[M].北京：电子工业出版社，2012.

[14] 李洋波，李 翔，黄达海.混凝土徐变度反演分析方法[J]. 三峡大学学报(自然科学版)，2005，27(2)：134-136.