节理倾角对砂岩强度及物理特征的影响

，， ，， (.三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 44300；.长江科学院 水利部岩土力学与工程重点实验室，武汉 43000)

1 研究背景

天然岩体中普遍存在着节理裂隙，且存在着许多不同类型的不连续面，包括片理、节理、层理面、裂隙、断层和剪切带，加上人工开挖、爆破、地震等众多因素对岩体的影响，使得节理岩体力学特性研究变得更为复杂。

目前已有许多学者通过室内、现场试验及数值模拟等方法对节理岩体力学特性进行深入研究。刘远明等[1-4]通过各种试验方法，对节理岩体的强度特性进行了研究；刘爱华等[5-6]等通过数值模拟的方式，研究了节理对岩体力学性质的影响；Kulatilake等[7]通过预制节理和裂隙的方法开展相似材料模型试验，研究了节理岩体的力学参数与岩体结构间的关系;王鲁明等[8-9]通过运用数值模拟和理论推导等手段开展应力波穿越节理岩体的能耗规律研究；陈新等[10]通过单轴压缩试验，系统地研究节理组的产状和节理连通率的连续变化对张开断续节理岩体单轴压缩强度和弹性模量及应力-应变曲线的影响;杨横涛等[11]通过FLAC3D建立数值计算模型，研究了单裂隙的几何参数对岩样破坏强度的影响;胡波等[12]采用理论分析同模型试验相结合的方法对共面闭合断续节理岩体的直剪强度特性进行研究；李庆森等[13]利用单轴压缩试验对经历不同温度后节理砂岩的物理力学性质进行分析研究，同时探讨不同温度对于变形破坏机理的影响;黄书岭等[14]通过利用其所提出的本构模型与三维节理网络模型，初步提出基于连续介质力学理论的合成岩体模型分析;Wang 等[15]以多组节理岩体为研究对象，提出了能够反映岩体强度和变形各向异性的节理岩体本构力学模型。

许多学者运用应力波测量岩石物理参数和通过试验以及数值模拟等方法对岩石峰值强度、应力-应变曲线和弹性模量进行了一系列研究，但在岩石物理和强度特征方面的研究较少。本文以三峡库区砂岩作为研究对象，通过完整及不同节理倾角(30°，60°，90°)的岩样在不同围压(0，5，10，20 MPa)下的三轴加载破坏试验及声波测试试验，探讨不同节理倾角对岩石物理特性的影响，得出不同节理倾角对岩样应力应变曲线和峰值强度的影响规律，同时通过Mohr-Coulomb准则和Hoek-Brown准则拟合主应力之间的关系。

2 试样制备及试验方案

2.1 试样制备

砂岩为典型的沉积岩，而沉积岩则是水文地质及地质区域的主要类型，砂岩在沉积岩中分布最广。砂岩一般由砂、基质、胶结物组成，砂岩中砂含量一般超过50%，碎屑以石英、长石为主。根据《水利水电工程岩石试验规程》(DLT 5368—2007)以及《工程岩体试验方法标准》(GB/T 50266—99)确定试样按100 mm×50 mm(长度×直径)圆柱体进行制备。取出岩芯用切割机切为2段,并分别将两端面切割磨平，制样严格按照国际岩石力学学会(ISRM)试验规程来加工，满足以下几点要求：①岩样直径的误差≤0.3 mm；②端面不平行度误差≤0.05 mm;③端面与试件轴线间最大偏差均≤0.25°。

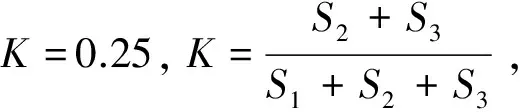
图1 连通率示意图Fig.1 Schematic diagram of connectivity

图2 部分制备岩样Fig.2 Some prepared specimens

2.2 试验方案

(1)在岩样切割节理前后分别采用非金属超声波检测分析仪对岩样进行声波测试，得出不同切割节理对岩样波速大小的影响。

(2)将岩样置于RMT-150C岩石力学试验系统上，使用应力控制，同步施加围压和轴压(施加速率均为0.1 MPa/s)至5，10，20 MPa( 围压和轴压相同)，使试样处于静水压力状态；然后保持围压不变，使用位移控制，速率为0.005 mm/s，使岩样加载至破坏。通过完整以及含有不同节理倾角(30°,60°,90°)砂岩的三轴压缩试验，并依此分析得到预制节理砂岩与完整砂岩的基本力学参数及强度特征。

3 物理特性分析

采用NM-4A非金属超声分析仪，测试之前保证岩样表面干净、平整，岩样与传感器之间涂抹凡士林，多次测量取最小值。纵波波速公式为

ν=L/Δt。

(1)

式中：ν为纵波波速(m/s)；L为岩样高度(m)，Δt为声波传播时差(s)。

通过对126个试样进行声波测试发现，岩样分布比较集中，在2 633～3 467 m/s之间，均值为3 050 m/s。绘制纵波波速散点图，如图3。

图3 完整试样纵波波速散点图Fig.3 Scatter plot of longitudinal wave velocity of intact rock specimens

通过对3组切割节理前后的岩样进行波速影响分析，得出不同节理岩样纵波波速变化规律，见表1。

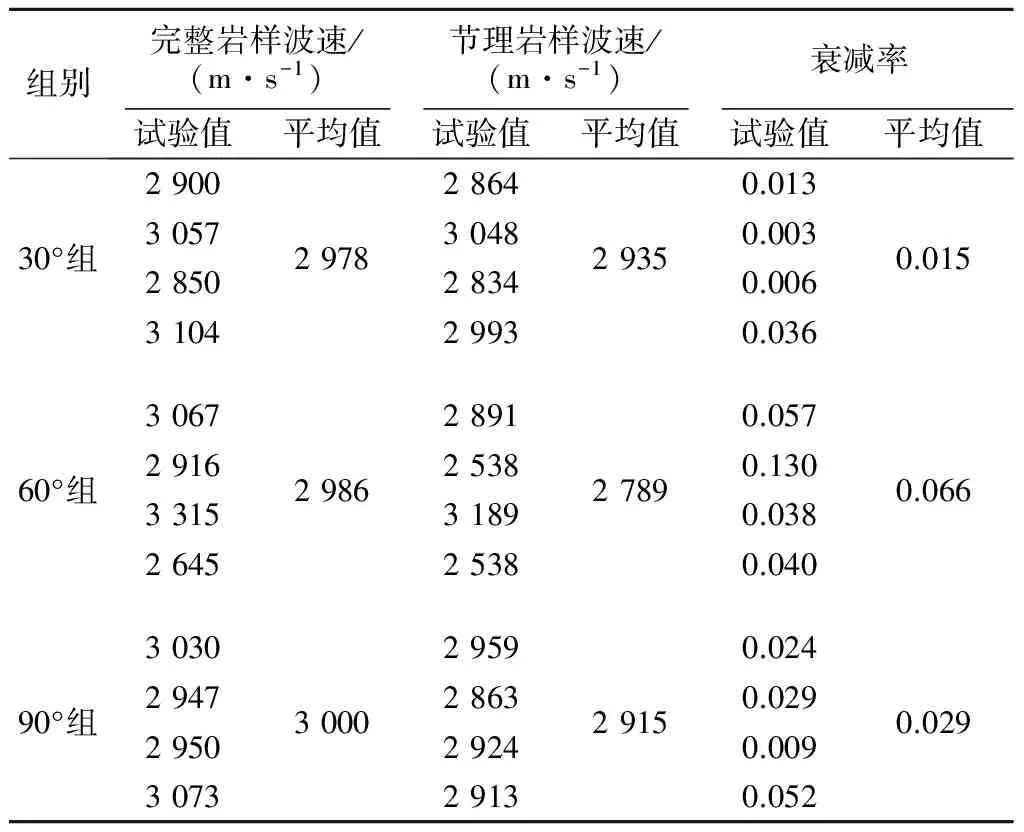
表1 不同节理岩样纵波波速Table 1 Longitudinal wave velocity of differentjointed rock specimens

注：衰减率=(完整岩样波速-节理岩样波速)/完整岩样波速

从表1中可以看出节理对岩样纵波波速有较大的影响。随着节理倾角的变化，岩样纵波波速衰减率有所不同，其中在节理倾角为60°时衰减率最大，在30°和90°时衰减率相对较小。

4 强度特征分析

4.1 强度理论与强度准则

岩石的峰值强度也表征岩石的极限承载能力，从岩石的峰值点则可以看出岩石材料在破坏时的应力以及应变的状态。岩石在一定的应力下，当试样一个方向上的应力增大直到岩石试样发生塑性破坏，岩石材料的应变就会随着应力的增加发生累积，当应力增加到岩石发生破坏时就会出现岩样的极限应力值，该极限应力值就是该条件下岩样的峰值强度。

将岩石的强度理论作为一种材料破坏判断依据，用来表征岩样在极限平衡状态时岩石内部应力应变与岩石相关参数之间的关系，采用主应力之间的关系可以表示为

F(σ1,σ2,σ3)=0 。

(2)

在岩土工程中，Mohr-Coulomb准则和Hoek-Brown准则是目前运用较为广泛且普遍接受的强度准则和强度理论，Mohr-Coulomb 准则中岩石的抗剪强度τs是由岩石的内摩擦角φ与黏聚力c共同确定的，包络线为直线，其关系式为

τs=c+σtanφ。

(3)

式中σ是岩石破坏面上受到的最大正应力，使用最大主应力σ1及最小主应力σ3表示时可写成

σ1=M+Nσ3。

(4)

式中M，N都是强度准则参数。M是该岩石的单轴抗压强度的理论值。M，N用试样的黏聚力c和内摩擦角φ分别表示为：

(5)

(6)

Hoek-Brown强度准则是在试验的基础上得到的经验强度准则，岩体破坏时最大主应力与最小主应力之间的关系式为

(7)

式中：m为经验参数；s为与岩体特征相关的常数；σc为单轴抗压强度值。通过公式换算可进一步将该式写成

(8)

4.2 应力-应变曲线

从图4应力-应变曲线中可以得出，在相同节理倾角下，岩样峰值强度随着围压的升高而增加，应力-应变曲线处于弹性阶段的线段也在逐渐变长，且达到峰值强度的时间也在逐渐增加；当围压较低时，岩体内部强度较低的部分先达到屈服强度而破坏，导致岩体内部产生裂隙，当轴向荷载继续增大时，岩体内部孔隙扩展并贯通，导致岩体破坏，但同时岩体内部强度较高的部分还未达到其屈服的强度；当围压升高时，限制了岩体低强度部分产生的塑性变形的发展，此时岩体内部较高强度的部分发挥承载作用，并发生弹塑性破坏，出现了较明显的屈服平台。随着围压的逐渐增大，岩样的竖向抗压承载力逐渐增强，岩样由脆性破坏向延性破坏转变，岩样塑性变形阶段增长，且应变也在逐渐变大。同时节理岩样的弹性模量均低于完整岩样，弹性模量随节理倾角的变化规律大致是E完整>E90°>E30°>E60°。

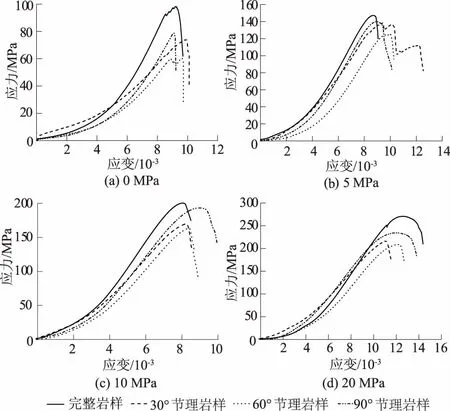
图4 不同倾角下节理岩样的应力-应变曲线Fig.4 Stress-strain curves of jointed rock specimens with different dip angles

4.3 峰值强度与节理角度的关系

在连通率为0.25时，非贯通节理岩体峰值强度随着节理倾角与围压的变化曲线如图5所示，结果显示:在该连通率下节理岩体的峰值强度均小于完整岩样;在同一节理倾角下，岩样的峰值强度随着围压的增加而增加；在同一围压下，岩样峰值随着节理倾角的变化表现出明显的各向异性，其规律表现为σ完整>σ90°>σ30°>σ60°。

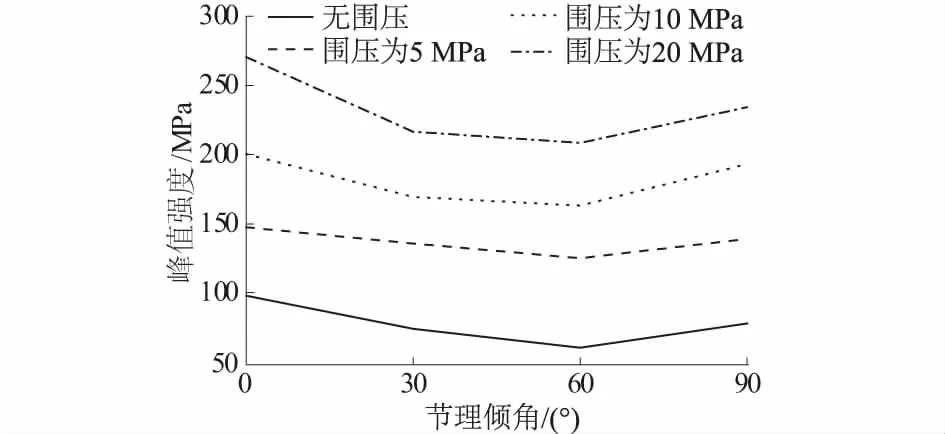
图5 节理岩样峰值强度随节理倾角的变化曲线Fig.5 Changes of peak strength of jointed rock specimens against dip angle

从图5中可以发现节理倾角对非贯通节理试件的峰值强度有较大影响，而岩样的峰值强度随着节理倾角β的变化呈现出U型的变化趋势，在已经完成的几组围压下最小峰值强度一般出现在节理倾角为60°处，由此可见节理倾角对峰值强度的影响较为明显。

4.4 峰值强度与围压的关系

不同节理倾角岩样的峰值强度随着围压变化的统计结果如图6所示。

图6 节理岩样峰值强度随围压的变化曲线Fig.6 Curves of peak strength of jointed rock specimens against confining pressure

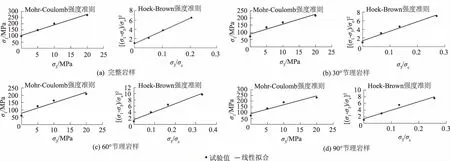
图7 完整岩样与不同倾角节理岩样峰值强度与围压的关系Fig.7 Relationship of peak strength of intact rock and jointed rock specimens with different dip angles against confining pressure

根据试验数据，使用Mohr-Coulomb准则和Hoek-Brown准则对已完成的各组围压下试样的峰值强度进行拟合，拟合结果如图7所示。分别采用上面2个强度准则对本次数据进行拟合，统计拟合结果的线性回归及拟合系数如表2所示。拟合结果表明，2个准则均能较好地表达主应力之间的关系。

表2 峰值强度线性回归公式及相关系数统计值Table 2 Linear regression formulae of peak strengthand values of corresponding correlation coefficient

根据Mohr-Coulomb准则，可得到岩样在峰值强度时的黏聚力c和内摩擦角φ，见表3。结果表明：节理岩样的黏聚力随着节理角度β的变化呈现出U型的变化趋势，且在节理角度β=60°时黏聚力最小，最小为14.50 MPa；同时内摩擦角随着节理角度β的增大而逐渐增大，最大值为52.36°。

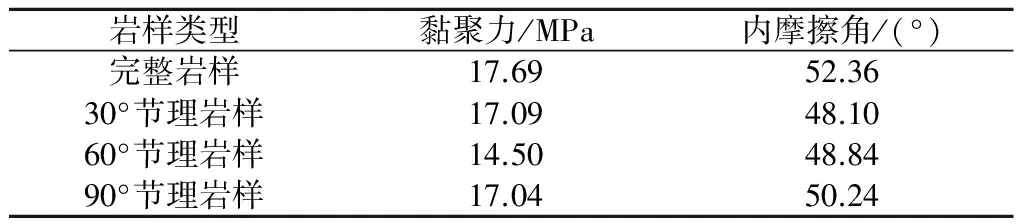
表3 岩样峰值强度下的黏聚力和内摩擦角Table 3 Cohesion and internal friction angle atpeak strength of rock specimens

5 结 论

通过完整及含不同节理倾角(30°，60°，90°)岩样在不同围压(0，5，10，20 MPa)下的三轴加载破坏试验及声波测试试验，研究了节理倾角对砂岩强度及物理特性的影响规律。研究结果表明：

(1)节理倾角对岩样纵波波速影响有较大的影响。随着节理倾角的变化，岩样纵波波速衰减率有所不同，其中在节理倾角为60°时衰减率最大，在30°和90°时衰减率相对较小。

(2)在围压较高时出现了较明显的屈服平台。节理岩样的弹性模量均低于完整岩样，弹性模量随节理倾角的变化规律大致是E完整>E90°>E30°>E60°。

(3)节理倾角对非贯通节理试件的峰值强度有较大影响，同一节理倾角下，岩样的峰值强度随着围压的增加而增加；同一围压下，岩样的峰值强度随着节理角度的变化表现出明显的各向异性，其规律表现为σ完整>σ90°>σ30°>σ60°。

(4)岩石峰值强度随围压的升高而增加，Mohr-Coulomb准则和Hoek-Brown准则均能较好地表达主应力之间的关系。节理岩样的黏聚力随节理倾角β的变化呈现出U型的变化趋势，节理倾角为60°时黏聚力最小；内摩擦角随着节理倾角增大而逐渐增大。

参考文献：

[1] 刘远明,刘 杰,夏才初. 不同节理表面形貌下非贯通节理岩体强度特性直剪试验研究[J]. 岩土力学,2014,35(5):1269-1274.

[2] 李海波,冯海鹏,刘 博. 不同剪切速率下岩石节理的强度特性研究[J]. 岩石力学与工程学报,2006,25(12):2435-2440.

[3] 张志刚,乔春生,李 晓. 单节理岩体强度试验研究[J]. 中国铁道科学,2007,28(4):34-39.

[4] 王 欣,宋卫东,王永清,等. 程潮铁矿矿岩节理面力学特性实验研究[J]. 矿业研究与开发,2011,(5):35-39.

[5] 刘爱华,董 蕾,董陇军. 节理岩体强度参数的数值模拟及工程应用[J]. 中南大学学报(自然科学版),2011,42(1):177-183.

[6] 盛 谦,黄正加,邬爱清. 三峡节理岩体力学性质的数值模拟试验[J]. 长江科学院院报,2001,18(1):35-37.

[7] KULATILAKE P H S W,MALAMA B,WANG J L.Physical and Particle Flow Modeling of Jointed Rock Block Behavior under Uniaxial Loading[J].International Journal of Rock Mechanics & Mining Science,2001,38(5):641-657.

[8] 王鲁明,赵 坚,华安增,等. 节理岩体中应力波传播规律研究的进展[J]. 岩土力学,2003,24(增2):602-605，610.

[9] 李业学,范建辉,李 铮. 岩体节理对应力波传播规律影响的研究进展[J]. 湖北文理学院学报,2015,36(11):10-14，22.

[10] 陈 新,廖志红,李德建. 节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J]. 岩石力学与工程学报,2011,30(4):781-789.

[11] 杨横涛,林 杭.岩样单裂隙几何参数对其破坏模式与强度的影响[J].长江科学院院报,2018,35(3):26-33,44.

[12] 胡 波,张 楠,王思敬,等. 断续节理岩体模型试验及强度分析研究[J]. 地下空间与工程学报,2011,7(4):657-665.

[13] 李庆森,杨圣奇,陈国飞. 高温后节理砂岩强度及变形破坏特性[J]. 煤炭学报,2014,39(4):651-657.

[14] 黄书岭,丁秀丽,邬爱清,等. 层状岩体多节理本构模型与试验验证[J]. 岩石力学与工程学报,2012,31(8):1627-1635.

[15] WANG Tai-tien, HUANG Tsan-hwei. A Constitutive Model for the Deformation of a Rock Mass Containing Sets of Ubiquitous Joints[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(6): 521-530.