基于Leaderrank的高拱坝场内施工道路复杂网络重要节点挖掘与分析

，， ， ,，(1.三峡大学 a.水利与环境学院; b.水电工程施工与管理湖北省重点实验室，湖北 宜昌 443002；2.中国葛洲坝集团股份有限公司 a.白鹤滩施工局,四川 凉山 615400; b.向家坝施工局，四川 宜宾 644000)

1 研究背景

高拱坝施工道路一般可划分为对内交通和对外交通，针对场内交通的特殊性与复杂性，本文重点研究高拱坝场内施工道路网络。不同于城市道路，高拱坝场内施工道路有其独特的特征：场内运输量大、运输强度高，多处于高山峡谷、地质条件复杂的山区，运输难度大；临时性、线路多变、多交叉口、多坡、多转弯；运输车辆多为大型车辆，有特重大件运输；通常没有行人和其他交通工具影响[1]。正是由于高拱坝场内施工道路的这些特点，使得其面临的不确定性因素众多，如地质灾害、路面损坏等，从而引起场内施工道路系统局部失效，致使整个系统超载并损害其整体功能，这种局部失效有可能传导至整个道路网络，造成道路交通运输能力和效率明显降低。因此，为了在施工道路发生局部失效后尽快恢复施工道路应有的功能，必须深刻认识路网拓扑性质，进一步研究施工道路网络的整体特性，在此基础上对施工道路网络进行控制与管理，以保证施工道路正常运行，满足工程施工需要。

目前关于高拱坝场内施工道路布置方面的研究很少，可以参考其他水利水电工程施工道路布置和城市道路布置研究。水利工程施工道路线型布置通常采用三次B样条曲线拟合[1]。刘序[2]建立了土石方调配模型，以此为基础对梨园堆石坝工程场内交通进行了仿真研究。关于城市道路的研究中，单条城市道路相关研究已经非常成熟，在交通优化方面(如分时、分路、分车型、分流向使用道路等)都有深入研究[3]；李清等[4]研究了道路可靠性，用遗传算法解决了最短和最可靠的路径搜索问题；Hirpa等[5]建立了优化道路三维设计的模型，并找到了效用和土方工程费用2个相矛盾目标的非支配解； Pushak等[6]运用多种离散算法寻找新公路最好的建设路径，提出了一种具体的优化算法。

在城市道路复杂网络分析中，张朋东等[7]提出了一种道路网络拓扑强度层次表达模型，为确定各路段在维持路网连通性方面的重要性程度提供了依据；赵玲[8]运用复杂网络对2种不同类型的路网，提出了一种基于交通流的建模方法； Zhang 等[9]研究了基于复杂网络的VANET拓扑分析，对道路堵塞、安全和管理方面的相关研究有所帮助。同时，在复杂网络鲁棒性和可靠性方面，张琨等[10]基于Pagerank算法提出了网络重要性评估的新指标； He等[11]研究了加权复杂网络的鲁棒性，发现影响网络鲁棒性的重要因素是连接强度。

总的来说，可以参照其他水利水电工程施工道路和城市道路布置的相关研究成果，对高拱坝施工道路进行布置，但是，从高拱坝施工道路的整体出发，分析施工道路网络的拓扑结构，确定施工道路中的重要节点，提高施工道路整体的鲁棒性和可靠性，还有待进一步深入研究。因此，本文运用复杂网络理论建立了高拱坝场内施工道路网络模型，采用Leaderrank算法对道路网络的重要节点进行挖掘，从而确定重要的施工道路，为施工道路受损时制定有效的恢复方案提供依据。

2 高拱坝场内施工道路网络模型建立

2.1 基本假设

根据上述高拱坝场内施工道路的特性，对本文建立的网络模型作出如下基本假设：

(1)场内施工道路的设计能够满足工程建设的各项要求，并且符合水利水电工程施工组织设计规范、公路工程技术标准等国家现行的规范。

(2)由于高拱坝场内施工道路不像城市道路那样具有详细的等级划分，因此假设各道路的等级相同且不存在单行线，即节点处于同一层级水平，所有节点都是双向连接。

(3)由于高拱坝场内施工道路所处地区一般为偏远山区，条件较城市道路更为复杂，不同于城市道路单个或多个交叉路口失效，施工道路更多的是道路失效，因此本文建立模型时将较长的道路划分为多个路段，考虑整个节点的失效。

(4)我国所处环境稳定，对城市道路网络大规模的蓄意破坏比较少见，对施工道路的蓄意破坏更为少见，但是自然灾害等不可预见的突发情况造成道路损害无法通行的情况时有发生，因此本文不考虑蓄意攻击或随机攻击对道路网络的影响，而重点关注破坏发生后如何更好、更快地恢复路网。

(5)由于高拱坝施工道路在空间上存在立体交叉，并且随着时间的推移会发生变化，但是目前的网络模型理论无法很好地解决这类问题，所以本文没有考虑高拱坝施工道路在时间上和空间上的变化，只是以高拱坝施工道路全部投入使用、道路网络规模最大的时期为依据，建立施工道路网络模型。

(6)假设道路破坏时没有大量人员伤亡，并且救援资源和条件有一定限制,即不可能同时修复所有受损道路。

2.2 道 路

网络模型中用节点表示道路，将施工道路网络各条道路、桥梁等抽象成为网络的节点，同时为避免出现带有重边或环的复图造成相关研究的困难，将施工网络当中长度较长且交叉口较多的道路进行划分，形成多个路段，每个路段用一个节点来表示。在这里，用V来表示节点的集合，V=[v1,v2,..,vn]。

2.3 交叉口

网络模型中用边表示交叉口，将道路之间的交叉口定义为边，那么边就表示道路之间的连接关系，根据道路网络的特性不存在孤立的节点。在这里定义，用E来表示边的集合，E=[e1,e2,...,em]。

2.4 施工道路网络模型

通过以上分析，可以将施工道路抽象成为1个无向的网络模型，包括节点集合和边集合2方面的信息，具体定义为：G=[V,E]。也就是一个由n个节点m条边组成的网络模型。网络模型的可视化可由Pajek软件获得[12]。

2.5 施工道路网络模型验证

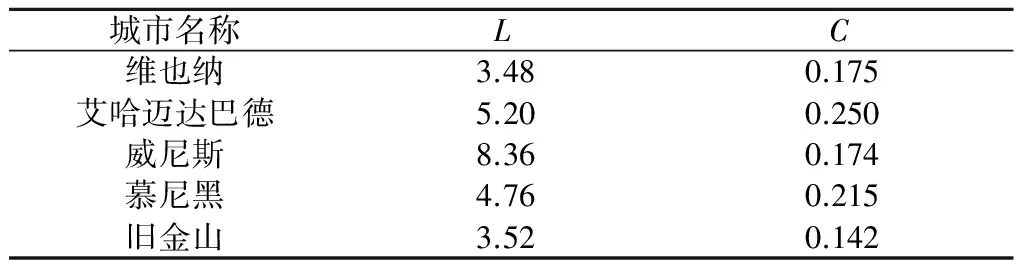
施工道路网络模型建立之后，需要验证是否符合复杂网络的相关特征。在这方面，城市道路的相关研究已比较完善，可以用平均路径距离、集聚系数来说明网络模型的特征，L表示平均路径距离，C表示集聚系数。目前已证明了城市道路具有小世界网络的特征，部分城市道路具有无标度网络的特征，文献[13-14]给出了一些城市道路网络特征值,见表1。

表1部分城市道路网络特征值
Table1Characteristicvaluesofroadnetworkinsomecities

城市名称LC维也纳3．480．175艾哈迈达巴德5．200．250威尼斯8．360．174慕尼黑4．760．215旧金山3．520．142

注:平均路径距离L没有单位，在复杂网络理论中，2个节点经历边数最小的一条路径为测地线，测地线的边数为节点距离，所有节点距离取平均为网络的平均距离L。比如，一个节点通过一条边与另外一个节点相连，它们之间的距离就为1

可以发现上述城市道路具有如下特征：相较于具有相同节点数的规则网络(比如只与相邻节点连接的最近邻耦合网络图)，城市道路网络的平均距离非常小，同时具有较高的集聚系数。本文将所算得高拱坝场内施工道路网络特征值与上述城市道路网络特征值进行对比分析。

如果施工道路的L和C具有与城市道路类似的特征，则可以考虑其是复杂网络且具有小世界网络的特征，可以进一步利用最为典型的小世界网络模型WS模型进行验证。根据施工道路网络模型，可以建立类似的节点数目相同的WS模型。WS模型的平均距离可以近似地由如式(1)获得。

(1)

式中：N为节点个数，每个节点与它左右相邻的B个节点相连,K=2B；p为随机化重连概率；f(u)为普适尺度函数,其近似表达式为

(2)

小世界网络的集聚系数可以表示为

(3)

对于大多数真实的复杂网络，WS模型的建造方式使得其与现实网络存在差距，但其表现出的一些性质、特点普遍存在于现实网络当中。如果高拱坝施工道路网络模型与WS模型的计算结果相似，那么就说明高拱坝施工道路网络是复杂网络。

3 施工道路网络重要节点挖掘

现实网络中的重要节点挖掘具有重大意义，也是复杂网络研究的热点之一，从目前的相关研究来看[15]，重要节点的挖掘没有一种通用的方法，都有其侧重点，需要对方法的准确性进行验证。

3.1 Leaderrank算法

本文考虑利用随机行走的思想来进行重要节点的挖掘，其中最为经典的是谷歌的Pagerank算法，但当网络中存在孤立节点或社团时结果可能不唯一，且收敛速度不快，因此本文采用了针对这些问题的改进算法,即Leaderrank算法[16]。

为方便对网络相关参数、特征进行计算，需要引入邻接矩阵的概念，具体的邻接矩阵A为

式中：aij表示节点vi和节点vj之间的连接关系，即若aij=1则表示存在1条从节点vi指向节点vj的边，反之aij=0，则表示2节点间不存在边。根据所研究施工道路网络的特征，建立的网络模型为无向图，因此上述邻接矩阵中aij=aji，且主对角线aii=0。需要注意的是，邻接矩阵主要反映两相邻节点之间的连接关系。

Leaderrank算法为1个有N个节点、M条边的网络图，额外增加一个节点G，且该节点与其他节点建立双向连接，即网络图变为有N+1个节点，M+2N条边的强连通的网络图。其具体的迭代步骤如下。

第1步：除了节点G以外的每个节点值si(0)=1，节点G的值sg(0)=0。

第2步：在时间t，节点i的分数为si(t)，为了方便计算,针对无向网络图对公式进行改写，则

(4)

式中Dj为节点j的度。

第3步：最后第2步的迭代会收敛于一个定值，此时将节点G的分数sg(tc)平均加入其他节点的分数中，可得节点的重要度为

(5)

式中tc表示式(4)收敛于定值时的迭代时间。

上述迭代过程中aij/Dj，即为一个随机的行走者在节点i处走到节点j处的概率，易证其构成的矩阵P为素阵，根据Perron-Frobenius定理，矩阵P的最大特征值有唯一的特征向量，因此算法的收敛性有保证，且快于Pagerank算法。

3.2 结果验证

重要度是一个非常模糊的概念，根据定义的不同，可能会造成结果的不同。因此，本文以节点失效后施工道路网络平均距离以及网络规模的变化来定义节点的重要度，具体的平均距离的变化反映节点间最短距离的变化，即部分道路失效之后剩余道路之间联系的最短距离；网络规模则反映节点失效后不可达节点的数量，即部分道路失效之后，不可到达的道路数量。由此可见，这2个指标能较好地反映道路失效后对整个道路网络的影响，从而挖掘出重要的道路。

本文采用删除与节点有关的所有边的方法，通过对比节点失效前后道路网络的变化，来验证排序结果的准确性。首先考虑按排序结果移除节点，步骤如下：

(1)初始化网络，此时网络的平均距离L0可以用Pajek软件算得，网络规模为s0=N。

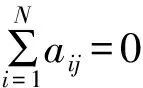
随后考虑节点的随机失效，计算方法与上述步骤类似，唯一不同的是在随机地移除节点而不是按照顺序，即随机使邻接矩阵中第i行第i列的所有元素变为0。

最后根据计算结果绘制平均距离和网络规模变化曲线，曲线横纵坐标均采用与原网络对比的相对值，通过对比分析所绘制的2条曲线，来验证结果的准确性。

4 实例应用

4.1 工程概况

某高拱坝位于云南省与四川省交界处，该工程场内施工道路名称以及道路之间的连接关系见表2。

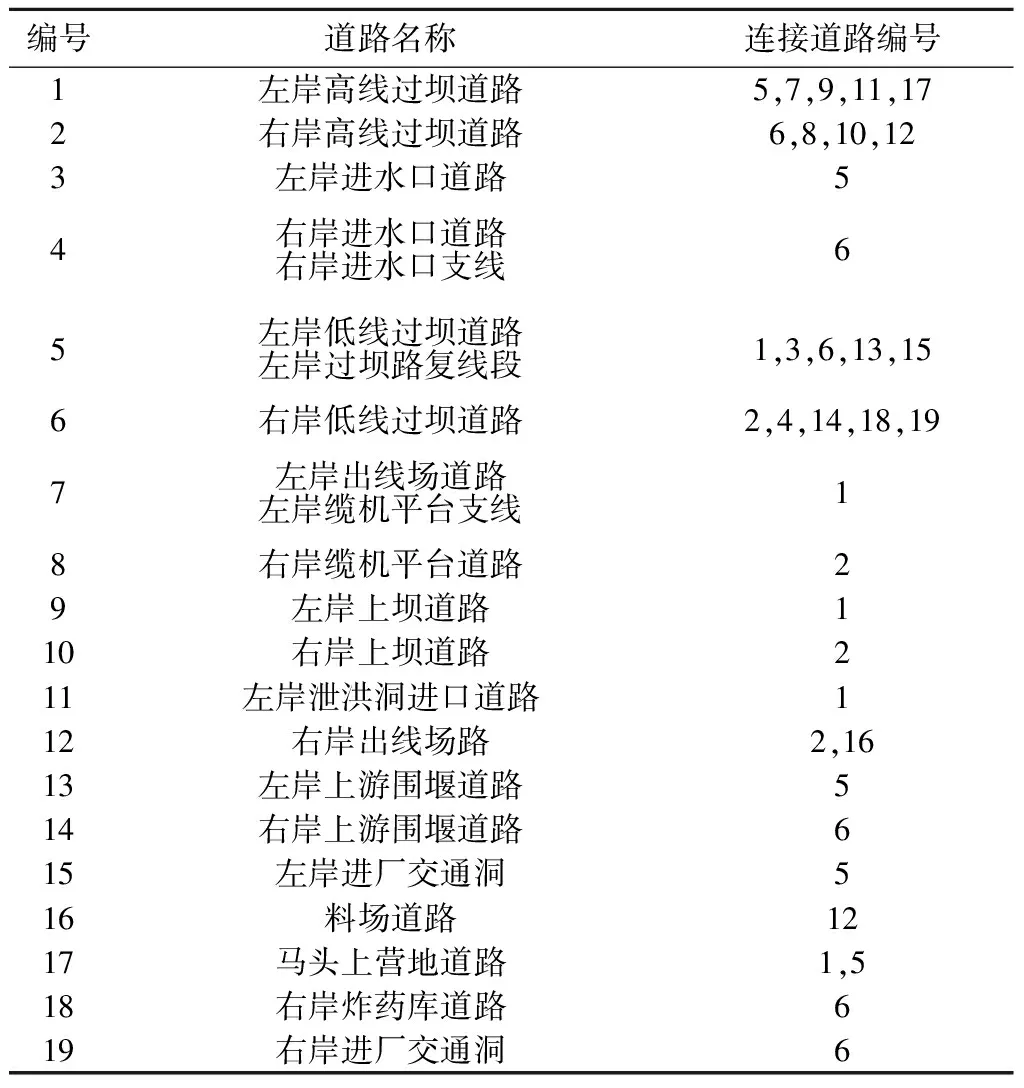
表2 场内施工道路一览表Table 2 List of roads in the construction site

4.2 高拱坝施工道路网络拓扑分析

在本工程中，存在一条道路有多个交叉口与另外一条道路相连接，如5号道路有2个交叉口与1号道路相连，5号道路与6号道路通过上游临时索道桥、下游临时索道桥和一座永久桥梁相连接，且交叉口之间距离较远，仅用1条边表示它们之间的关系显然不太合理;其次应避免所建网络图模型出现重边等复图，不利于后面对网络图进行分析的情况；再次灾害发生时，对于这些特殊的道路而言，整条道路失效的可能性较小，更多的是部分路段或者几个交叉口失效，在网络图中具体的表现是边的失效，简单地移除节点不能反映实际情况，增加了分析的难度。因此，为简化分析步骤，同时不失科学性，本文将几条比较长的道路,根据交叉口分为几个路段，分别将5号道路、6号道路按上游索道桥位置分成2个路段，索道桥看成单独的道路，在网络图中用单独的节点表示。

根据以上道路信息，利用复杂网络分析软件Pajek将该高拱坝施工道路抽象成为一个具有23个节点的网络图，结果见图1，需要验证该网络模型是否符合复杂网络的特征。

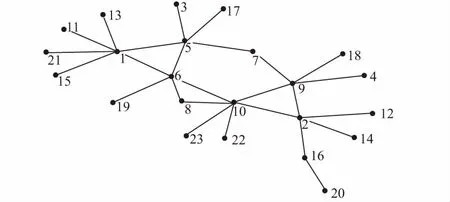
图1 施工道路网络图Fig.1 Construction road network

针对上述网络进行基本几何特征量的计算可得：该网络的平均路径距离L=3.024；该网络的集聚系数C=0.189。

通过对比表1的城市道路相关特征值，发现施工道路网络在数值上与城市网络较为接近，有类似的地方，可以考虑场内施工道路具有小世界网络的特性。

根据本工程实际情况，构建类似的WS模型。取N=23，K=4，p=0.5为具体参数构建WS小世界模型。根据式(1)平均距离L=2.334，根据式(3)集聚系数C=0.188，可以发现高拱坝施工道路模型的值与其非常接近。

综上所述，通过高拱坝施工道路网络和城市网络与WS小世界网络的对比研究，可以发现该高拱坝施工道路网络是一个复杂网络，且具有小世界网络的特性，至于这种特性是否普遍存在于施工道路网络中还需要更多实例的支撑。

4.3 施工路网重要节点挖掘及验证

通过上述分析已了解了该高拱坝施工道路网络的特性，下面需要对网络中的重要节点进行挖掘，并对整个道路网络的节点进行排序，具体的算法已经由3.1节给出。由于邻接矩阵为24阶的矩阵，在这里将其列举出来意义不大，故在此省去，网络图经过增加一个节点的变化见图2。

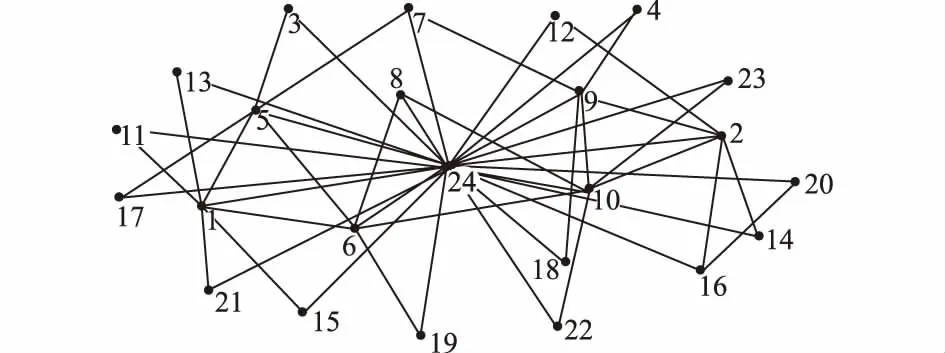
图2 变化后的施工道路网路图Fig.2 Modified construction road network

根据式(4)和式(5)，利用MatLab进行编程迭代计算，计算结果如表3所示。

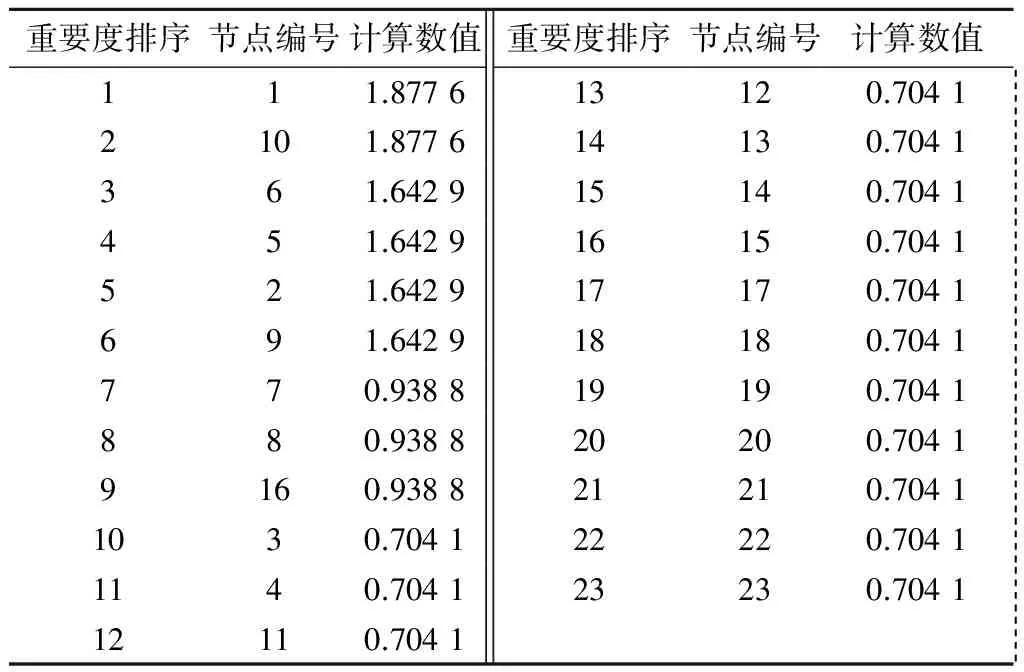
表3 道路节点得分结果Table 3 Scores of road nodes

图3 施工道路网络平均距离对比Fig.3 Comparison of average distance among construction roads between different node-failure modes

对上述结果进行进一步验证，方法已由3.2节给出，对比节点随机失效和按排序顺序使节点失效对道路网络平均距离和连通性(主要表现在网络规模的变化，不可达节点数量)的影响。

从图3可以看出，按排序节点失效曲线，在初始阶段平均距离随着节点失效呈现上升的趋势，但随着更多的节点失效，平均距离迅速下降，这主要是因为道路网络的连通性不断下降，不可达节点数量迅速增加，使得网络的规模迅速缩小。由于节点数目很少，剩余部分的平均距离迅速下降，随着重要节点的失效，断裂节点为初始网络节点的0.35左右,整个道路网络就已经完全失效；节点随机失效曲线，在初始阶段平均距离的变化较为平稳，且与原网络基本一致，随着大量节点失效，平均距离也迅速减小，直到变为0。

从图4可以看出，按排序节点失效曲线对比于节点随机失效曲线，网络规模缩小得更快，与平均距离曲线图一致，重要节点失效后，道路网络完全失效；从节点随机失效曲线来看，网络规模变化情况基本呈现出线性递减的形式，且大部分节点都失效后，整个道路网络才彻底失效。

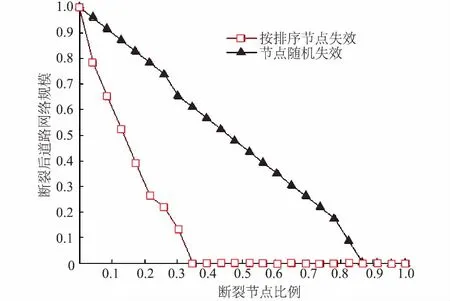
图4 施工道路网络规模对比Fig.4 Comparison of network scale of construction roads between different node-failure modes

综上所述，采用Leaderrank算法在施工道路网络重要节点挖掘中较为准确，通过删除节点的边的方式进行分析、对比，可以发现该算法识别的重要节点在网络中具有重要的意义，如果识别的重要节点失效，对整个网络的平均距离、规模有非常大的影响。

5 结 语

本文将施工道路网络抽象化，建立施工道路网络模型，将所建模型应用于工程实例中，通过计算相关特征值发现施工道路网络具有小世界网络的特性，进一步研究了网络节点重要度排序，并通过节点删除法验证了排序结果的准确性，最终找出了重要的施工道路。在施工道路受到损坏时，为道路的抢修顺序，尽快恢复施工道路网络的功能提供依据。

在本文实例当中出现了许多重要度赋值相同的节点，这主要是由于在本案例中，有多个仅有1个交叉口的道路与同一条重要道路相连，这也是造成重要节点失效后整个施工道路网络迅速瘫痪的原因之一。由此可见，本研究是寻找最优的施工道路网络结构、增强施工道路网络鲁棒性的研究基础，这也是下一步需要进行的工作。

参考文献：

[1] 冯志军，郭 潇，张玉峰,等. 水利水电工程施工场地布置决策理论、方法与应用研究[M]. 郑州: 黄河水利出版社, 2010.

[2] 刘 序.梨园面板堆石坝交通仿真分析研究[D].天津：天津大学，2014.

[3] 《中国公路学报》编辑部. 中国交通工程学术研究综述·2016[J]. 中国公路学报, 2016,29(6):1-161.

[4] 李 清, 胡志华. 基于多目标遗传算法的灾后可靠路径选择[J]. 浙江大学学报(工学版), 2016，(1):33-40.

[5] HIRPA D, HARE W, LUCET Y,etal. A Bi-objective Optimization Framework for Three-dimensional Road Alignment Design[J]. Transportation Research Part C: Emerging Technologies, 2016,65:61-78.

[6] PUSHAK Y, HARE W, LUCET Y. Multiple-path Selection for New Highway Alignments using Discrete Algorithms[J]. European Journal of Operational Research, 2016, 248(2): 415-427.

[7] 张朋东, 石 岩, 邓 敏, 等. 基于拓扑强度的城市道路网络层次表达[J]. 武汉大学学报(信息科学版), 2016，(2):178-183.

[8] 赵 玲. 城市道路网络结构分析及其对交通流的影响研究[D]. 长沙：中南大学, 2013.

[9] ZHANG Hong, LI Jie. Modeling and Dynamical Topology Properties of VANET Based on Complex Networks Theory[J]. AIP Advances, 2015,5(1):17150.

[10] 张 琨, 李配配, 朱保平, 等. 基于Pagerank的有向加权复杂网络节点重要性评估方法[J]. 南京航空航天大学学报,2013,45(3):429-434.

[11] HE Zhi-wei, LIU Shuai, ZHAN Meng. Dynamical Robustness Analysis of Weighted Complex Networks[J]. Physica A: Statistical Mechanics and Its Applications, 2013,392(18):4181-4191.

[12] 诺 伊, 姆尔瓦, 巴塔盖尔吉. 蜘蛛：社会网络分析技术[M]. 林 枫，译.北京: 世界图书出版公司, 2014.

[13] JIANG B, CLARAMUNT C. Topological Analysis of Urban Street Networks[J]. Environment and Planning B: Planning and Design, 2004,31(1):151-162.

[14] PORTA S, CRUCITTI P, LATORA V. The Network Analysis of Urban Streets: A Dual Approach[J]. Physica A: Statistical Mechanics and Its Applications, 2006,369(2):853-866.

[15] 刘建国, 任卓明, 郭 强, 等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013，(17):9-18.

[16] LÜ Lin-yuan, ZHANG Yi-cheng, YEUNG C H,etal. Leaders in Social Networks, the Delicious Case[J]. PLOS ONE, 2011,6(6):e21202.