桃林口水库下游山区洪水演进模拟和洪灾损失评估
2018-06-15天津大学水利工程仿真与安全国家重点实验室天津30007河北省桃林口水库管理局河北秦皇岛066000
, ,,,(.天津大学 水利工程仿真与安全国家重点实验室,天津 30007;.河北省桃林口水库管理局,河北 秦皇岛 066000)
1 研究背景
洪水演进数值模拟作为防洪减灾体系中的重要部分,是流域生命安全和经济发展的重要保障,为洪水预警、洪灾风险评估等提供依据。近年来,随着山洪造成的伤亡和损失不断攀升,山区洪水风险逐步引起国内外专家和政府关注。对于山区洪水的特性及山区洪水的数值模拟,已有诸多专家和学者进行了研究。张光科[1]对山区河流特性作初步探究;吴修广等[2]提出山区河流二维糙率计算公式,并应用于二维水流计算中;李艳红等[3]提出“混合五对角法”建立平面二维数学模型,解决山区河流复杂边界及计算稳定性等问题;解刚[4]利用贴体网格建立了适用于山区河流的平面二维推移质模型,并用有限差分ADI法离散方程;陈一帆等[5]基于三角形无结构网格的有限体积法建立了耦合水工建筑物的山区河流平面二维模型;张红萍[6]基于GIS技术建立了山区小流域洪水评价机制,为山区小流域洪水风险评估提供技术支持;韩通等[7]引入K最近邻算法应用于山区小流域洪水实时校正。
与平原地区相比,山区洪水数值模拟存在较多困难。由于山区地形的约束及山区汇流特征的影响,山区洪水流速变化快,水位暴涨暴落,对模型求解稳定性造成一定影响,对时间步长的限制较为严格。且由于山区地形起伏较大,在模型计算过程中更容易产生水流虚假流动的现象,影响模型计算的稳定性和准确性。此外,山区洪水调查难度较大,历史洪水资料不够完整,洪灾损失统计资料不够完善,防洪评价工作较难开展。
本文以二维非恒定流方程为基本理论建立模型,采用有限体积法对网格进行离散求解。通过对水量平衡计算模式的修正,解决单元虚假流速的问题。根据桃林口水库的实际地形、地貌和水库泄洪过程,模拟了洪水演进过程,并根据实际情况提出相应的评价方法,对该地区洪灾风险进行评估。
2 数学模型基本理论
2.1 二维非恒定流控制方程
连续方程:
(1)
动量方程:
(2)
(3)
式中:H为水深;M,N分别为x,y方向上的单宽流量,且M=Hu,N=Hv;u,v分别为x,y方向上的平均流速;q为源汇项;n为糙率系数;z为水位,z=z0+H,z0为底高程;g为重力加速度。
2.2 有限体积离散
按照有限体积法布置二维网格的方式如图1所示。取单元网格为控制体,在网格中心计算水位H,在网格周边通道的中点计算流量Q。即在平衡计算时,控制体每条边的法向通量用该边中点处的通量作代表,乘以边长即为通量沿该边的积分。中点的通量可用中心格式(如取相邻两格子形心处通量的平均)或逆风格式确定。
2.2.1 连续型方程离散
将方程(1)改写成矢量形式,按照有限体积法,将其在控制体内进行积分,对水位和流量按时间交错计算方式(如图1(b)),则方程(1)可离散为
(4)
式中:Ai为第i个网格的单元面积;Lik为i号网格的第k号通道的长度;Qik为i号网格的第k号通道的单宽流量。
2.2.2 运动方程离散
由于山区河道实际地形较为复杂,对运动方程进行离散时可将复杂的地形概化为地面型通道、河道型通道和缺口堤或连续堤通道,并给所有通道附加特征信息,以相应的水力学公式进行计算。
(1)地面型通道,即通道两侧单元为陆地地面,且地形起伏不大。此时地形对水流形态的影响较小,洪水演进主要受到重力和阻力的作用,加速度项可忽略不计。通过差分法离散可得到地面型通道的动量离散方程为
(5)
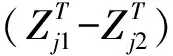
(2)河道型通道,即通道两侧网格均为河道型网格,此时洪水演进需考虑河道的复杂地形对水流的影响,因此动量方程中需保留局地加速度项、重力项和阻力项,利用差分方法离散得到河道型通道的动量离散方程为
(6)
(3)对于堤防、公路、铁路等高于地面的阻水建筑物,其流量通常采用宽顶堰溢流公式来计算,离散后得到
(7)
式中:σs为淹没系数;m为流量系数。
2.3 水量平衡计算模式
由于山区地形起伏大,山区河道洪水演进模拟计算过程中往往比平原河道更易出现虚假流动的现象,即单元出流量大于入流量,单元出现负水深。本模型网格为无结构的三角形网格,以图2所示为例对模型水量平衡计算模式进行说明。其中O为中心单元,H,HA,HB,HC为T时刻单元水深,QA,QB,QC为T+dt时刻由方程离散格式计算得到的通道流量。

图2 水量平衡计算示意图Fig.2 Schematic diagram of water balance calculation
当由式(4)计算得到的T+2dt时刻单元水深为负时,重新计算T+dt时刻的出流,根据计算得到的负水深(-h)分别将出流量按比例缩减得到QB1和QC1,保证中心单元O内不出现负水深;假定此时修正后的入流量为QA1,按此时中心单元O向B,C单元的出流比例重新分配,得到出流修正值QB2和QC2,保证QB2≤QB与QC2≤QC;按上一步骤得到的出流对单元O入流重新修正,再将入流量按比例分配给出流量,保证出流量不大于连续性方程计算值[8-9]。
3 数学模型构建
本文利用桃林口水库下游1982年1∶10 000比例尺地形图历史资料确定模型边界,以GIS平台资料和2012年河道平面、断面资料进行补充,建立二维洪水演进模型。
3.1 计算区域简介
桃林口水库位于青龙河中游,水库坝址位于青龙河干流河道上,库区位于河北省青龙县附近,控制青龙河流域面积的80%。桃林口水库相对位置示意图如图3所示。

图3 桃林口水库库区示意图Fig.3 Map of Taolinkou reservoir area
模型选取桃林口水库坝下青龙河与沙河汇流前的部分流域,计算区域覆盖面积约227.9 km2,由山区和丘陵组成,海拔高度在50~400 m之间(图4)。青龙河流域地处燕山山脉的暴雨中心地带,洪水主要由暴雨形成,由于暴雨历时短、强度大,地面坡陡流急,一次洪水过程表现为峰高、量大、陡涨陡落的特点。2012年7月21日,持续强降雨导致桃林口水库爆发5次连续的洪水,最大入库洪峰流量4 000 m3/s,至7月30日入库洪水总量11.10亿 m3,接近设计10 a一遇洪水。库区洪水调度后,水库泄洪将对大坝下游区域防洪安全产生重大影响。

图4 模型区域地形等值线Fig.4 Topographic contour map of model domain
3.2 模型区域网格划分
考虑计算区域边界的复杂性以及河道蜿蜒的走向,网格应对边界有较强的适应能力,因此模型采用无结构的三角形网格来离散计算区域。单元最小面积1 508 m2,最小边长38 m,网格节点12 956个,网格单元15 683个,网格通道28 638个。河道型网格节点15 683个。计算区域网格分布如图5所示 。

图5 模型区域网格划分Fig.5 Grid subdivision of model domain
3.3 模型边界条件
模型采用桃林口水库2012年7月31日15:00至2012年8月6日15:00时段内大坝泄流作为计算区域入流边界,泄流过程见图6(a)(横坐标中时间表示水库泄洪时间),其中最大泄量出现在8月4日1:00~4:00,洪峰流量为3 000 m3/s;模型下游边界采用青龙河与沙河汇流前河道断面的水位流量关系曲线,见图6(b)。
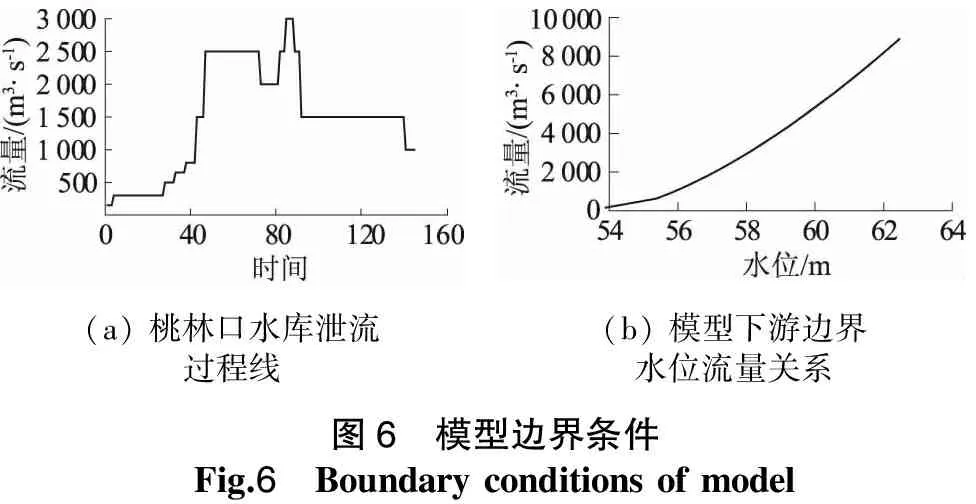
(a)桃林口水库泄流过程线(b)模型下游边界水位流量关系图6 模型边界条件Fig.6 Boundaryconditionsofmodel
4 模型验证
4.1 糙率系数取值
糙率是反映河床及其他下垫面对水流阻力影响的综合参数,其取值直接影响水力计算的准确性和精度。根据模型区实际的地物特征将模型单元划分为不同类型,并通过模型计算调试确定糙率取值。模型糙率取值结果见表1。

表1 二维模型糙率取值Table 1 Roughness values of two-dimension model
4.2 洪水演进验证
采用2012年8月历史最大洪水的演进情况对模型进行验证。选取模型计算第25,50,75,125 h的计算结果来反映洪峰到达前后洪水流速和淹没范围的变化情况,模拟结果见图7。
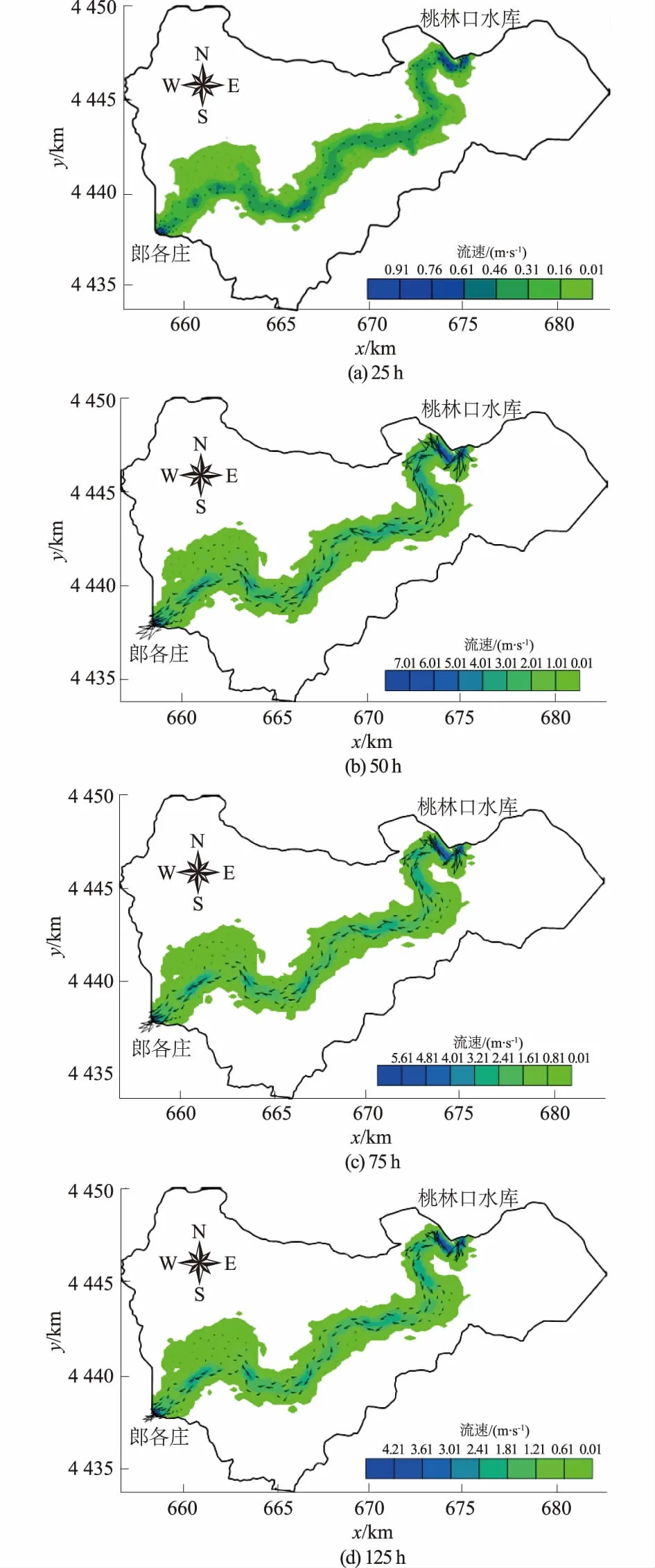
图7 洪水演进过程流场及淹没范围Fig.7 Flow fields and submerged area in flood routing process
从淹没范围来看,由于山区地形的约束,淹没范围并没有随来流的变化而明显变化。河道上游段河谷狭窄且坡度较陡,淹没水面相对不宽;下游段两岸坡度变缓,淹没水面逐渐展宽。从流场变化上看,随水库下泄流量由小变大再变小的过程,流场也随之变化。说明模型基本能够反映流场及淹没范围的变化趋势,模型构建基本合理。
洪水过后当地实测洪痕点的相对位置见图8。选取其中可靠程度高的洪痕点作为验证条件,将水位计算值与实测值作对比,进一步验证模型的准确性,验证结果见表2。从验证结果来看,水位计算值与实测值基本相差0.3 m以内。产生误差的原因是计算区域地形复杂,网格插值造成的误差使模型较难完全准确地还原当地地形、地貌及糙率等条件。但模型能够较合理地反映该区域洪水演进的趋势,且计算水位误差不大,说明模型参数选择准确,模型基本能反映洪水演进过程,可用于该区域洪水风险研究。

图8 模型水位验证点Fig.8 Verification of water level in the model

表2 左岸和右岸水位验证Table 2 Verification of water level on the left bankand the right bank
5 洪灾损失分析
5.1 洪灾经济损失评估
洪灾经济损失一般可归纳为直接损失和间接损失两方面。本文主要对洪灾造成的直接经济损失(即财产损失)进行分析和估算。由于财产损失与洪水淹没程度相关,因此本文根据模型计算得到的洪水最大淹没水深(图9)将受灾区域划分为5个风险等级,并归纳财产损失率与风险等级的二维关系[10],确定具体产业在不同风险等级下的财产损失率,结果见表3。
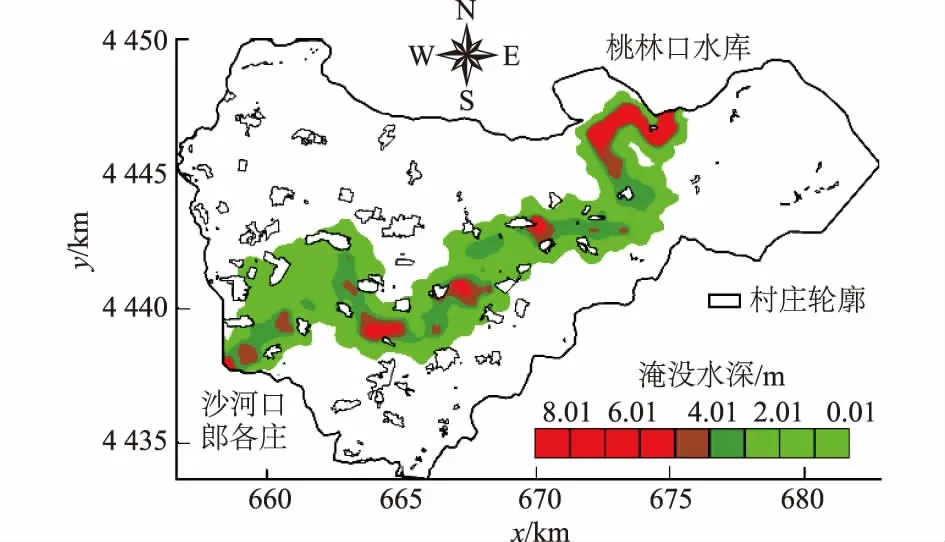
图9 模型最大淹没范围及淹没水深Fig.9 Maximum submerged area and submerged depth

表3 洪水风险等级与财产损失率的关系Table 3 Relations between the risk level of flood andthe rate of economic loss
根据卢龙县统计年鉴的相关资料统计卢龙县受灾村庄的农、林、牧、渔业产值。依据受灾区域风险等级划分及每个风险等级对应的财产损失率,分别计算卢龙县各个受灾村庄的财产损失,计算结果如表4所示。
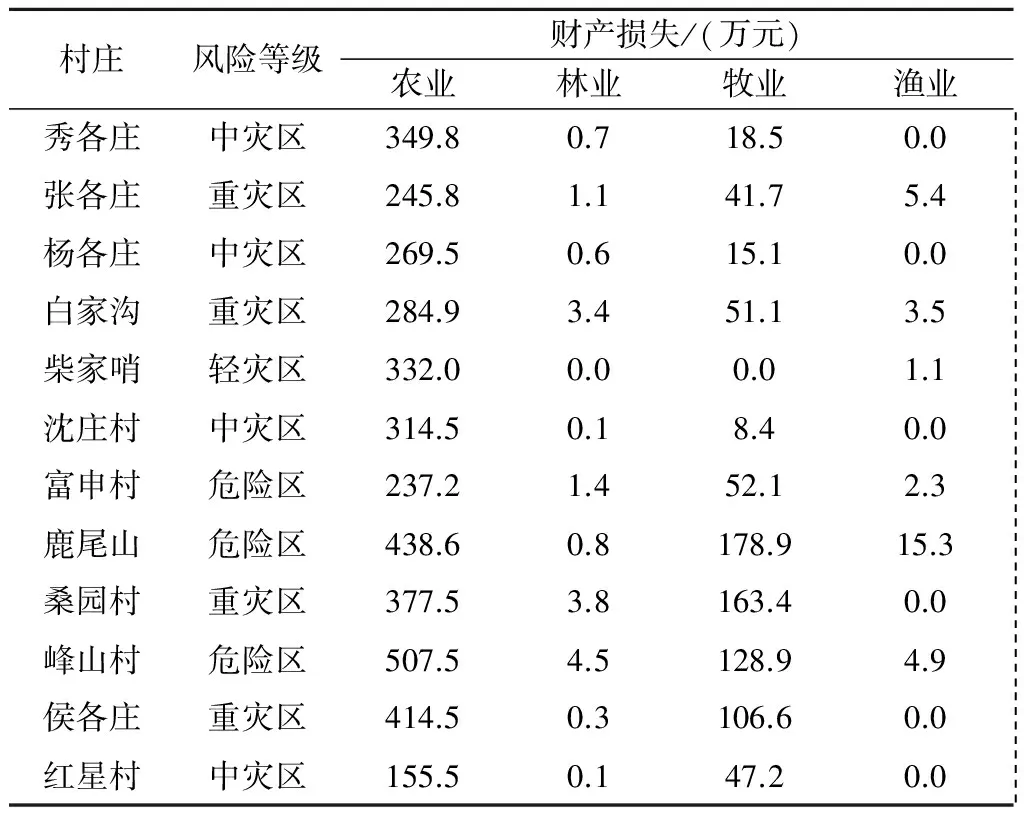
表4 卢龙县村庄财产损失统计Table 4 Statistics of economic loss in villages ofLulong county
5.2 洪灾生命损失分析
人员伤亡在洪灾损失研究中有重大意义。DeKay与McClelland根据大量的洪灾历史统计资料[11],利用对数回归分析总结出一个包含风险总人口、预警时间、洪水风险特征的生命损失估算公式,即
LOL=PAR/[1+13.077(PAR0.440)]·
1/[exp(0.759WT-3.709F+0.223WTF)] 。(9)
式中:LOL为洪灾生命损失数;PAR为风险总人口;WT为洪水预警时间;F为洪水风险特征,对高水力风险洪水取1,低水力风险洪水取0。
D & M公式在计算洪灾生命损失时虽然考虑了洪水风险特征的影响,但对于洪水风险特征F的取值方法较粗糙,导致对生命损失的估算结果存在很大的随意性。李大鸣等[12]提出,F的取值可以用淹没水深表征,且F的取值应与WT相关。考虑模型区洪水演进受山区地形约束,水面并没有展开,而仅表现在水深和流速的变化上,因此可用该区域滞水总体积与入流总体积的比值近似代替水深对风险特征F的影响。本文在计算洪灾生命损失时,应用洪水风险特征F的修订公式来反映F与WT之间的关系,即
F=(AX/AL)exp(-WT) 。
(10)
式中:AX为区域内滞水总体积;AL为区域内入流总体积。
根据模型计算,桃林口水库坝下山区在2012年7月31日到8月6日洪水过程中,入流总体积为21.19万m3,出流总体积为19.31万m3,区域内滞水总体积为1.88万m3。由公式(9)计算得到的洪水风险特征值见表5。根据区域内村庄受灾情况及人口统计数据可得各村庄的风险人口,统计乡镇地区风险总人口数,利用修订后的公式对洪灾生命损失数进行预测,计算结果见表6。
综合表5和表6的计算结果可以看出,在无预警(WT= 0 h)时,洪水将造成严重的人员伤亡;当0

表5 不同预警时间下F取值Table 5 Values of F in different warning time

表6 不同预警时间下伤亡人数Table 6 Casualties prediction in different warning time
6 结 论
(1)本文以二维非恒定流控制方程为基础建立桃林口水库下游山区洪水演进模型,通过有限体积法对方程离散求解,并以修正的水量平衡模式解决单元负水深的问题,提高了计算精度。
(2)采用河道两岸洪痕实测数据作为模型验证条件,验证点水位计算误差基本在0.3 m以内,验证结果表明模型参数设置准确,基本能准确模拟计算区域洪水演进过程;计算得到的淹没面积、淹没水深和流场结果较为合理,可为该区域防洪减灾及灾害评估提供可靠的依据。
(3)本文在模拟洪水演进过程的基础上,利用统计资料对区域洪灾财产损失进行了估算;通过改进洪水风险特征的取值方法对洪灾生命损失进行预测和评估,计算结果表明,预警时间在1.5 h内洪灾生命损失数明显下降,计算结果反映的趋势基本合理,但对经验公式的修订仍需考虑更多因素的影响,对风险估算结果仍需做进一步验证。
参考文献:
[1] 张光科.山区河流若干特性研究[J].四川大学学报(工程科学版),1999,3(1):11-20.
[2] 吴修广,王平义.山区河流二维阻力特性研究[J].重庆交通学院学报,2001,20(3):102-105,109.
[3] 李艳红,周华君,时 钟.山区河流平面二维流场的数值模拟[J]. 水科学进展,2003,14(4):424-429.
[4] 解 刚.山区河流平面二维泥沙数学模型[D].成都:四川大学,2004.
[5] 陈一帆,程伟平,蒋建群,等.含水工建筑物的山区河流二维流场数值模拟[J].浙江大学学报(工学版),2013,47(11):1945-1950.
[6] 张红萍. 山区小流域洪水风险评估与预瞀技术研究[D]. 北京:中国水利水电科学研究院,2012.
[7] 韩 通,李致家,刘开磊,等.山区小流域洪水预报实时校正研究[J].河海大学学报(自然科学版),2015,43(3):208-214.
[8] 杨紫佩.小清河蓄滞洪区洪水演进数学模型及水量平衡研究[D].天津:天津大学,2014.
[9] 李大鸣,范 玉,杨紫佩,等. 小清河滞洪区洪水演进数学模型的研究[J]. 天津大学学报(自然科学与工程技术版),2016,49(4):401-407.
[10] 李谢辉,韩荟芬. 河南省黄河中下游地区洪灾损失评估与预测[J]. 灾害学,2014,29(1):87-92.
[11] 周克发. 溃坝生命损失分析方法研究[D]. 南京:南京水利科学研究院,2006.
[12] 李大鸣,范 玉,赵明雨,等. 基于洪水演进数值模拟的洪灾生命损失计算方法研究[J]. 水利水电技术,2015,46(10):17-21.
