减速流条件下床面泥沙起动试验研究

，， ，，(长江科学院 .长江工程技术公司；.河流研究所，武汉 430010)

1 研究背景

长久以来，诸多学者对于均匀流条件下的泥沙起动做了大量的工作，并取得了许多成果[1-3]。但对于天然河流，特别是河道上修建有大量水闸、大坝及桥梁的河流，由于这些水工建筑物的挡水作用，使得沿程水深逐渐增加从而形成壅水，即形成减速流，且沿程非均匀性逐步加强，使得现有的计算公式不足以很好地表达该条件下的床面泥沙起动，因此，通过概化水槽试验的手段来研究减速流条件下的床面泥沙起动是很有必要的。

水流底部床面上泥沙开始运动称为起动，相应的水流泥沙条件称为起动条件。当泥沙颗粒的粒径、密度等已知时，泥沙开始运动的流速和水深称为起动时的流速和水深。由于水深对流速的影响较大，习惯上将水深作为参数，而将泥沙起动的流速条件称为起动流速。由于作用在泥沙颗粒上的流速是水流的底部流速，而在实际应用当中多换算成沿水深的平均流速，故起动流速应泛指这2种流速。在本项研究中，取沿水深的平均流速作为起动流速。

表示泥沙起动的条件除起动流速和水深外，尚有另外2种指标。其中在欧美应用较多的是起动拖曳力，即泥沙开始运动时床面底部水流切应力τc为

(1)

式中：ρ为水的密度；u*c为摩阻流速；g为重力加速度；h为水深；J为能坡，一般可用水面比降代替；γ为水的重度。τc与起动流速Vc(垂线平均流速)的换算关系为

(2)

另外一种起动条件指标是起动功率，其计算式为

Wc=γhJVc=τcVc=γqcJ。

(3)

式中：Wc为起动功率;qc为单宽流量。

起动功率表示单位宽度、单位长度的水体在单位时间内所损失的势能。后面通过试验结果分别对几种起动指标进行描述。

2 试验概况

2.1 试验水槽及设备

试验水槽采用矩形横断面，长50 m、宽1 m、高1 m，有效试验段36 m。试验水槽通过WJGS-2河工模型试验综合控制系统进行控制，该系统通过变频供水控制与计算机控制技术相结合，实现了流量、水位的全过程自动控制，减少了试验的强度，改善了控制精度，流量测量精度为0.5%，控制精度为2%。

水流循环系统由水泵、输水管路、试验水槽及其蓄水水库组成的封闭自循环系统；通过水泵从蓄水水库中提水至输水管路，然后注入水槽前池，再经水槽又流入蓄水水库，水槽前部加设3道花墙以平稳水流，水槽尾部通过尾门控制尾水水位达到调节各种壅水效果。水位用测针测量(精度为0.1 mm)，流速采用声学多普勒流速仪(ADV)测量。试验段尾部有集沙坎，试验水槽示意图见图1。

图1 试验水槽布置Fig.1 Layout of experiment flume

2.2 试验方案及试验条件

本试验主要研究不同均匀性下减速流床面泥沙的起动水槽试验。主要观测沿程水深、比降、流速以及泥沙起动的各种状态，底坡1.5‰，选定了3级流量(80，120，160 L/s)。非均匀性越强，同一工况流量条件下流速越小，对应的泥沙起动就越困难。为了依次观察到克雷默标准提出的床沙弱动、中动和普动效果[1]，每级流量均从最大水深处放起，床面铺沙15 cm，尾门处对应清水试验最大水深定为45 cm。若床面无泥沙颗粒起动，则降低水位，至观察到有少量泥沙颗粒起动，则记下时间，待水流稳定，放水1～2 h停泵，取不同水位下，固定断面的泥沙沙样进行筛分，得到对应的泥沙起动粒径。本试验采用粒径范围为0.125～10 mm的天然黄沙。通过预备试验后，得到每级流量下床面泥沙分别处于弱动、中动和普动状态下的组次，每组试验条件见表1。

表1 水槽试验条件Table 1 Parameters of flume experiments

注：h0为均匀流条件下正常水深，R为水力半径

在每组试验过程中，为保证试验条件不变，每次试验结束后，均会重新进行铺沙，然后进行下一次试验。每一级流量后，都需将水槽内黄沙清出槽外。重新搅拌均匀再填入水槽进行试验。每组试验结束后均需将积沙坎沙样以及沿程固定断面所取沙样进行烘干、称重，进行级配分析。

3 试验结果分析

3.1 非均匀性标准β

判别水流流态均匀性与非均匀性的通常方法是判断沿程水深是否发生变化。若水深发生变化则判别水流流态为非均匀，不变则为均匀流。对于减速流而言，沿程水深逐渐增加，各断面的水力条件显然发生变化。Graf等[4]提出了非均匀系数βn，即

(4)

式中：dh/dx为沿程水深变化率；S为床面底坡;τ为床面切应力。水槽试验当中，由于水面的波动，水面比降测量并不精确，同时床面切应力也不能准确确定，因此该参数在实际应用当中并不是十分理想。

本试验主要是研究非均匀性对床面泥沙起动的影响，因此可以取非均匀断面水深与正常水深即均匀流水深的比值作为该水流的非均匀系数β[5],即

(5)

由此可以计算出A，B，C三组试验条件下的非均匀系数β，见表2。

表2 非均匀参数β计算结果Table 2 Calculation results of heterogeneityparameter β

3.2 起动标准

依据定性的克雷默标准来分析泥沙起动，显得主观性较强，而且随意性极大，即使是相同的标准，具体的判断也会因人而异。为了使试验达到更高的精度，选取一个合适的定量起动标准与定性标准相结合尤为重要。

对于推移质泥沙的起动标准，较为常用的就是韩其为等[6]提出的低输沙率的标准，确定相对输沙率λqb，c=0.219×10-3为起动标准，但在计算过程中需要以起动颗数来算单宽输沙率，在现行试验条件下达不到特定的精度。考虑到所选沙样级配较宽(0.125～10 mm)，为了减小试验的复杂程度，选取推移质取样标准作为起动标准[7-8]，即推移质累计频率接近100%(95%左右)的粒径确定为起动粒径。

图2为试验得到的各工况条件下，积沙坎处表层泥沙取样后，烘干、筛分做出的累计频率曲线。筛分采用0.125～10 mm的连续筛。为了保证起动标准的精确性，根据数值分析中样条插值法，在各曲线中内插累计频率95%，得到对应的d95粒径值。

图2 A,B,C三组试验取样泥沙级配曲线Fig.2 Gradation curves of sediment in test group A,B, and C

同时，可发现在不同流量下，泥沙起动粒径随着水深的变化有着相同的规律，随着壅水指标的变大，起动粒径变小，沿程会出现粗沙先起动细沙后起动的现象。钱宁等[1]研究表明粗沙先动细沙后动的现象与2种沙的隐暴系数有关系。

3.3 临界起动流速公式参数验证

指数型起动流速公式为

(6)

式中:Uc为所测断面平均流速;d为粒径，取起动标准粒径d95;h为对应水深;γs为泥沙的重度;A为起动流速参数。

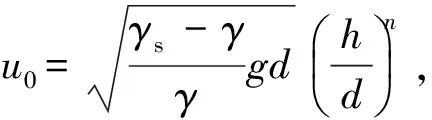
由图3可知，当n取1/6时，参数A在1.06～1.38之间拟合近似为一条直线。沙莫夫公式和张瑞瑾公式化简形式中的参数A分别为1.14和1.33，均在此范围内。

表3 起动流速参数A计算结果Table 3 Calculation results of incipient flow velocityparameter A

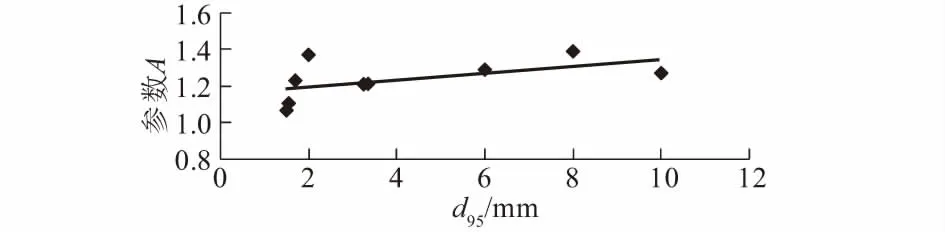
图3 起动参数A与起动粒径的关系Fig.3 Relationship between incipient parameter A and incipient particle size

图4 万县水文站实测资料起动流速验证Fig.4 Verification of incipient velocity of measured data at Wanxian hydrological station

同一流量下参数A随着水深的变化略有变化，总体上，随着壅水指标的变大有略微减小的趋势。可以推断，在水槽试验中，指数起动公式中的参数A是一个常数，对于本水槽参数A取值为1.23。即起动流速公式可定义为

(7)

若引入非均匀系数β，h=βh0，即

(8)

对于指数型流速公式,其计算粒径d通常选用d50，但根据对实测资料数据整理分析，结果不够理想。将d50和d95分别代入式(7)对万县水文站实测资料中的起动流速进行验证。如图4所示，对比2种粒径标准，d95计算结果更满足实际的起动流速。因此，可以说明在非均匀性较强的条件下，选用d95作为起动粒径其结果更加精确。

3.4 临界无量纲拖曳力参数验证

前面已经指出，表达泥沙起动的临界水流条件的另一种形式为起动拖曳力。对于临界起动拖曳力的描述，最著名的就是希尔兹(A.Shields)起动拖曳力公式[1]，即

(9)

其中，

(10)

式中：τ0c为临界拖曳力;U*为摩阻流速;ν为运动黏滞系数;Θc为临界相对拖曳力；Re*为沙粒雷诺数。

由式(9)可以看出，临界相对拖曳力Θc和沙粒雷诺数Re*是最主要的2个参数。将9组试验数据分别代入式(9)得到结果见表4。

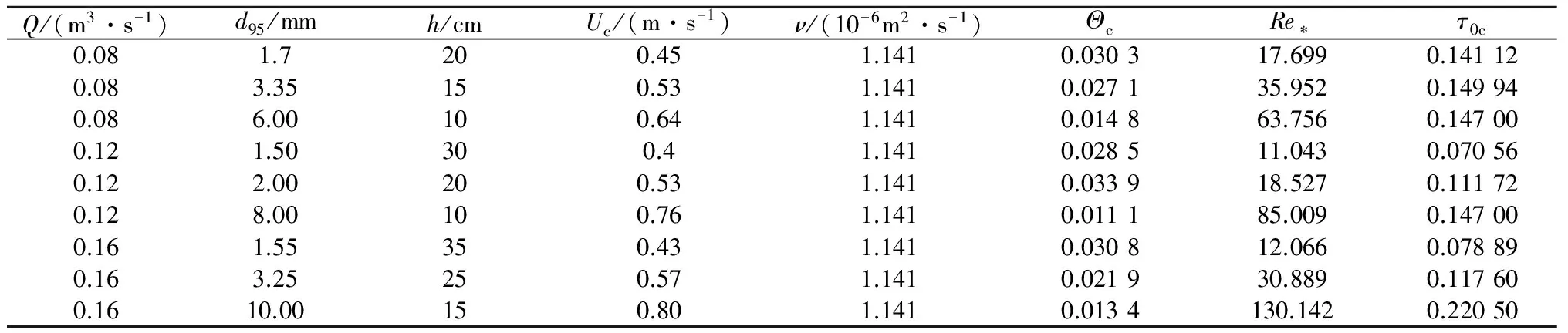
表4 水槽试验拖曳力参数计算结果Table 4 Calculation results of drag force parameters for flume experiments

Θc与Re*的关系如图5所示。可以看出水槽试验中，相对光滑度较大，沙粒雷诺数在11～130之间，临界起动拖曳力在0.011～0.339之间，试验点基本围绕在希尔兹曲线两侧。

图5 临界起动拖曳力与沙粒雷诺数的关系Fig.5 Relationship between critical drag force and Reynolds number of sand particles

引入非均匀性系数β，起动拖曳力τ0=γβh0J,随着水深的加大，β变大，比降J减小。由表4可知，起动拖曳力τ0是减小的，而临界相对拖曳力Θc呈现增大的趋势，说明起动拖曳力τ0受比降J的影响更大。而临界相对拖曳力Θc在一定范围内与β指标正相关。

3.5 临界起动功率分析

单位宽度和长度的水体在单位时间内所损失的势能为

W0=γhJU=γqcJ。

(11)

拜格诺[9](Bagnold)根据美国水道试验站的试验，用中值粒径为0.59 mm的泥沙得出的结果，推导出关系式为

(12)

式中：gb为推移质单宽输沙;K为比例常数。

因此，从功率的角度，泥沙的起动条件可表示为

(常数) 。

(13)

式中D为床面的物质组成。

在一定的比降下，式(13)可以写成

(14)

对于天然沙来说，有

(15)

Schoklitsch[10]曾根据水槽试验得出起动条件为

(16)

对式(13)作进一步的变形，在水槽试验中，比降J、水槽宽度B、床面的物质组成D是一定的。当流量较小时，泥沙不起动，保持其他参数不变，加大流量，水流的切应力就会变大；达到一定程度，泥沙起动，此时达到临界状态，这些参数之间必然能形成一个封闭的函数，可表达为

G(Q,D,B,J)=0 。

(17)

将式(17)转化为无量纲形式，矩形水槽宽度固定，即水面宽度固定，流量Q可用单宽流量qc来代替，则有

(18)

即无量纲流量为

(19)

根据表5的水槽试验结果，得到泥沙起动临界单宽无量纲流量q*c与水面比降Jc的关系见图6，可以看出，相关性较好，得到拟合关系式为

q*c=0.019 1Jc-1。

(20)

表5 水槽试验功率参数计算结果Table 5 Calculation result of power parameters offlume experiment

图6 泥沙起动参数J与q*的关系Fig.6 Relationship between sediment’s incipient parameters J and q*

设起动单宽水流功率的无量纲数W*c=q*cJc，则代入式(20)有W*c=0.019 1。该常数与Schoklitsch[10]得到的常数十分相近，可以作为泥沙是否起动的标准。

3.6 常用流速起动公式在水槽试验中的验证

传统公式中比较有代表性的成果有张瑞瑾、窦国仁，唐存本、韩其为等的起动流速公式，这些公式均以单颗粒的受力分析为基础，考虑了颗粒之间的粘结力，得到了粗细颗粒统一的起动流速的表达式。各家公式表达形式见表6。

将水槽试验数据分别用d95和d50作为代表粒径代入表6中的公式计算，结果见表7、表8，并将计算流速与底部实测流速相互验证,结果见图7。

表6 常用4家经典公式Table 6 Four commonly-used formulae

注：δ,εk根据交叉石英丝试验结果取δ=0.213×104cm,εk=2.56 cm2/s2;Ks为床面粗糙高度；D*为参考粒径

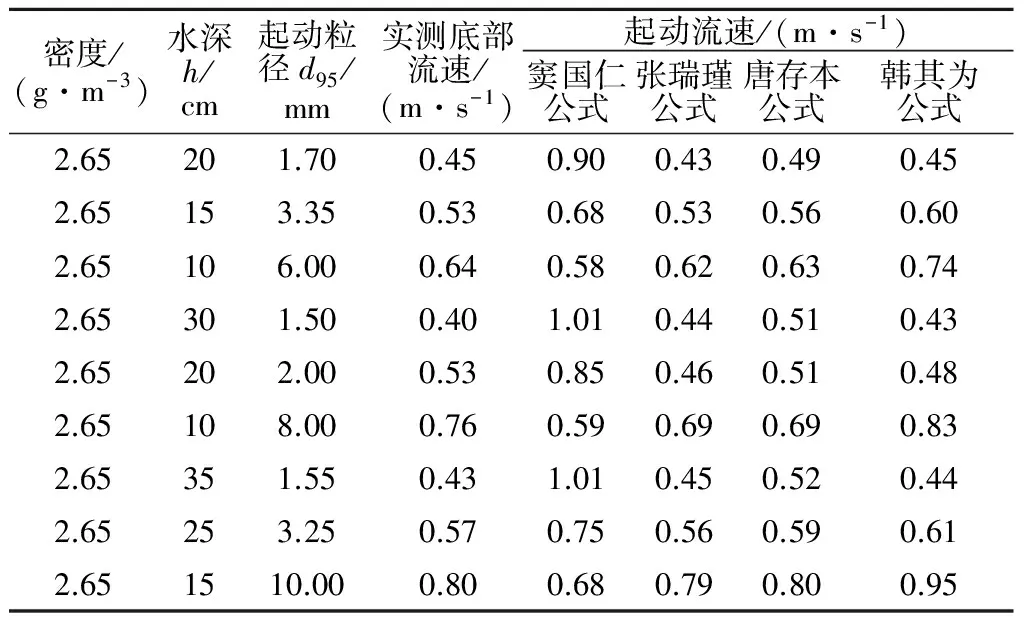
表7 以d95作为代表粒径的各家流速起动公式计算结果Table 7 Calculation results of each formula withd95 as representative particle size

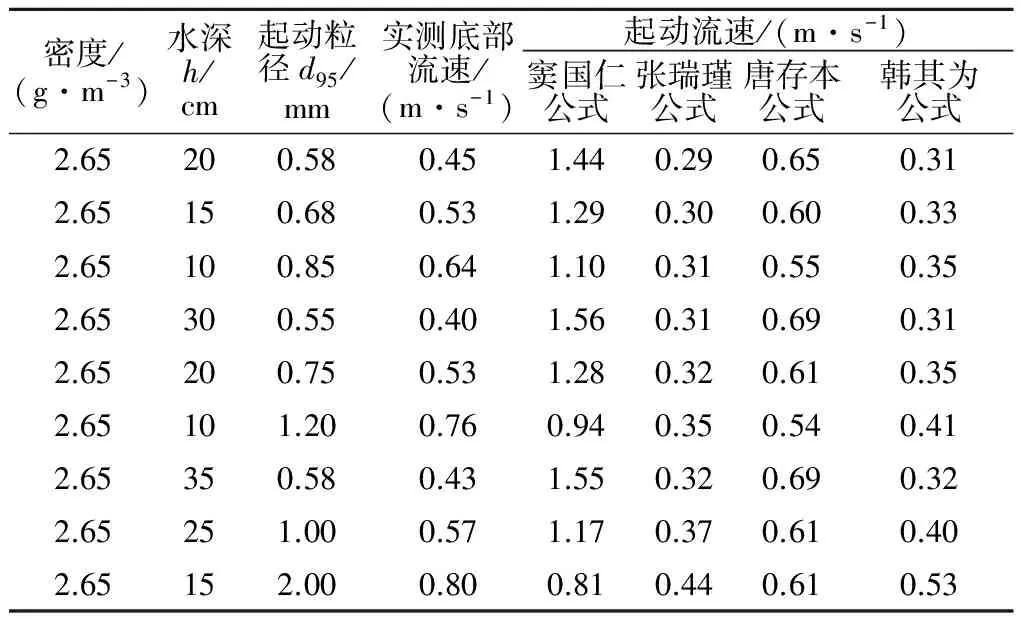
表8 以d50作为代表粒径的各家流速起动公式计算结果Table 8 Calculation results of each formula withd50 as representative particle size

图7 水槽实测底部流速与各家公式计算流速对比Fig．7 Flowratescalculatedbydifferentformulaeincomparisonwithmeasuredbottomflowrate

由图7(a)可知，水槽试验的起动结果与各家的起动流速公式计算结果较为接近。其中与张瑞瑾公式的符合程度最高，其次是韩其为和唐存本公式，窦国仁公式的差异性较大。

本试验选择取样标准作为起动标准，且起动代表粒径选用d95，通过对比图7(a)与图7(b)可知，对于减速流条件下的床面泥沙起动，选择d95较d50计算结果更加精确。

4 结 论

(1)对于减速流条件下的床面泥沙起动标准选取取样标准，即选择d95作为起动的代表粒径，具有较好的精确性。

(3)减速流水槽试验结果大体满足希尔兹曲线，起动拖曳力τ0受比降J的影响较大，而临界相对拖曳力Θc在一定范围内与非均匀系数β正相关。

(4)根据功率起动公式验证水槽试验，得到无量纲起动功率为0.019 1，可以将其作为床面泥沙起动标准。

(5)现有的4家经典公式对于减速流条件下的水槽试验泥沙起动有一定的差异性，这种差异性与非均匀性系数β的关系还需要进一步研究。

参考文献：

[1] 钱 宁，万兆惠. 泥沙动力学[M]. 北京: 北京出版社, 2003.

[2] 张瑞瑾. 河流泥沙动力学[M]. 北京: 中国水利水电出版社, 1989.

[3] 韩其为，何明民. 泥沙起动规律及起动流速[M]. 北京: 科学出版社, 1999.

[4] GRAF W H，ALTINAKAR M. Hydraulique Fluviale，Tome I [M]. Lausanne：Presses Polytechniques et Universitaires Romandes, 1993.

[5] 金中武，徐军辉，吴华莉. 壅水条件下水流阻力实验研究[J]. 长江科学院院报，2015, 32(4): 45-50.

[6] 韩其为，何明民，王崇浩. 卵石起动流速研究[J]. 长江科学院院报,1996, 13(2): 17-22.

[7] 吴宪生. 宽级配非均匀沙床沙双峰型的形成条件及起动规律[D]. 成都: 成都科技大学, 1984.

[8] 王兴奎，陈稚聪，张 仁. 长江寸滩站卵石推移质的运动规律[J]. 水利学报，1992，(4):32-38.

[9] 惠遇甲，胡春宏. Bagnold 推移质输沙理论中有关参数的探讨[J]. 泥沙研究, 1991,(3): 9-19.

[10] SCHOKLITSCH A. Der Geschiebeb and Die Geschie Befracht [J]. Wasserkraft and Wasserwirtschaft，1934, 29(4): 37-43.

[11] 张瑞瑾，谢鉴衡，陈文彪. 河流动力学[M]. 北京: 中国工业出版社, 1961.

[12] 窦国仁. 论泥沙启动流速[J]. 水利学报，1960，(4): 44-60.

[13] 唐存本. 泥沙起动规律[J]. 水利学报，1963，(3): 1-12.