基于振冲器理论模型的振动特性研究

2018-06-14王立强唐添

机械工程师 2018年6期

王立强，唐添

（沈阳化工大学，沈阳110142）

0 引言

随着经济发展，高大建筑越来越多；同时由于我国土地面积广阔，地基土质复杂，要对建筑地基进行加固处理，以很好地抵抗沉降以及地震产生的土壤液化，为建筑物提供一个稳定的基础[1]。振冲法（振动水冲法）是一种快速、经济有效的加固方法[2]。其原理是以起重机吊起振冲器，电动机带动偏心块转动，产生高频振动；同时通过喷嘴喷射高压水流，在振动和水冲的共同作用下，将振动器沉到土中的预定深度，从地面向孔内逐段填入碎石，使其在振动作用下被挤密实，达到要求的密实度后即可提升振动器，如此反复直至地面，在地基中形成一个大直径的密实桩体与原地基构成复合地基，提高地基承载力，减少沉降。本研究目标是为了通过理论分析与实验分析以及ANSYS模拟仿真对振冲器的振动特性进行研究，利用共振理论提高振动效率的同时，避免共振的发生[3-6]。

目前有关振冲器的振动特性方面所涉及到的理论分析中，基本上只是考虑了振冲器的摆动，而振冲器在实际的工作中不仅有摆动，还存在振冲器的弹性振动，这正是本论文的创新之处，无论是对于振冲器工作中避免共振情况的出现，还是对于促进动力学的发展，都具有重要的理论意义和实际意义。同时，考虑了弹性振动和摆动所得出的结论也会有助于论证文中理论模型的可行性[7-8]。

对振冲器的振动特性的5个参数，即电动机上端质量、偏心质量、起重机吊起钢丝绳长度、振冲器总长度和横截面积进行理论与实验研究，根据振冲器的临界转速建立边界条件从而建立动力学方程，通过理论计算、实验分析以及仿真模拟比较各种结果是我们主要的研究内容。

1 实验装置

实验设备如图1所示。支撑架通过细绳连接一根长700 mm，宽20 mm，厚度为2 mm的梁，梁相当于振冲器，细绳相当于起重机吊起钢丝绳，顶端和底部的质量相当于顶端的电动机和底部偏心的质量。在该实验中，上端部分的质量是固定的，而绳长、底部偏心质量是变化的，以此来测出固有频率，得出实验结论。为了测量梁的固有频率，应变片产生的信号放大后经过数据采集器，被电脑保存并分析。

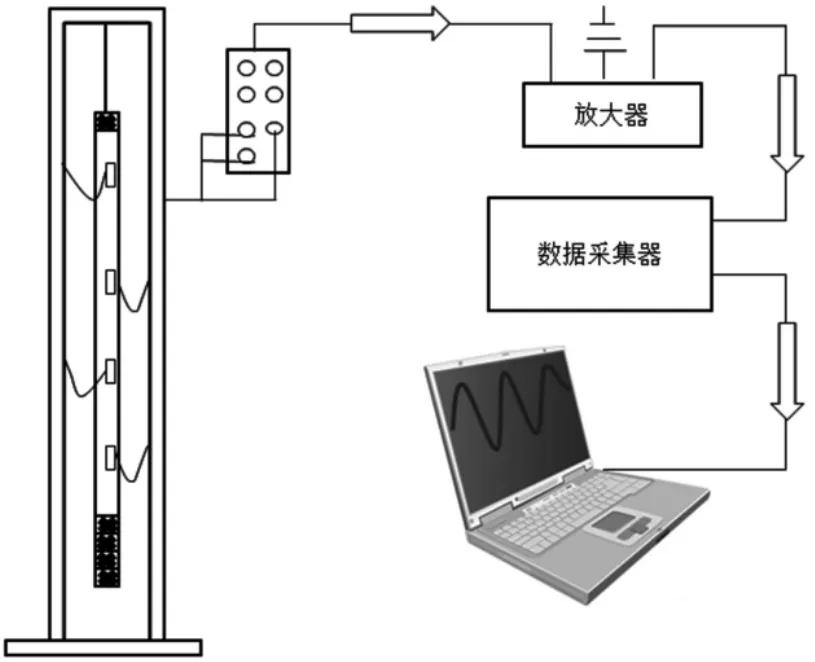
图1 实验装置

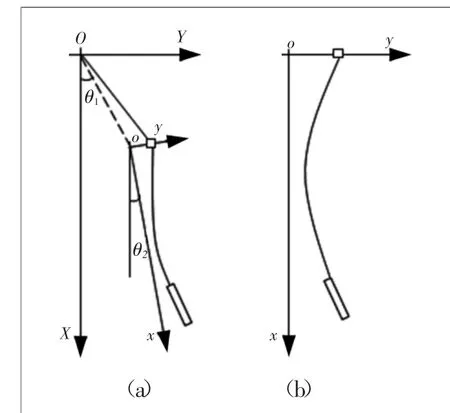
图2 理论分析的坐标系统

2 理论分析

本课题研究的主体是处理振冲器的弯曲振动有关的边界条件。在以往有关振冲器振动特性的文献中，这些边界条件没有清晰地给出。如果知道了梁的上端边界条件，就可以得出梁的固有频率。图2表示理论分析的坐标系统。图2（a）XOY为梁的摆动以及横向振动的复合坐标，图2（b）xoy为弹性振动坐标。对图2坐标系中振动分析的控制方程为

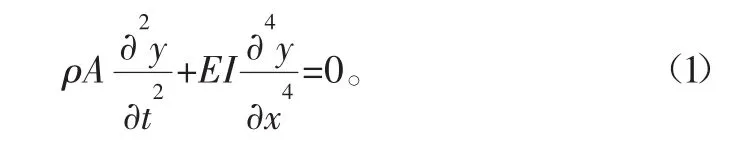
式中：E为弹性模量;I为截面惯性矩;ρ为密度;A为横截面积。

运用分离变量法[9-11]。

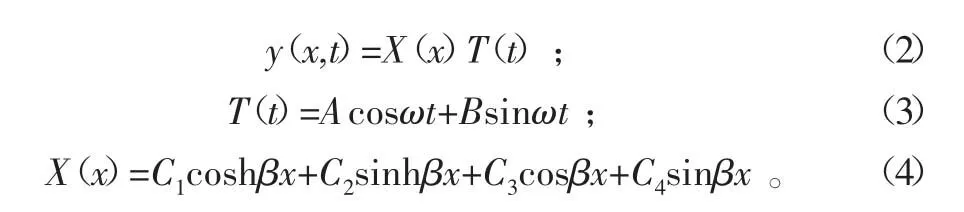
其中，

其中，ω为角固有频率。

在顶端（x=0）,力矩M为0；剪切力S由悬绳上惯性力和重力的总载荷决定。

力矩：

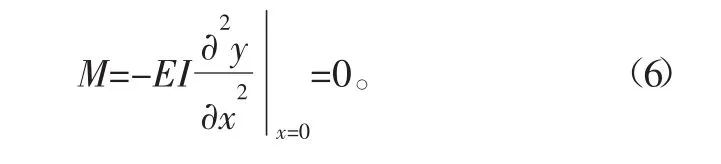
剪切力：

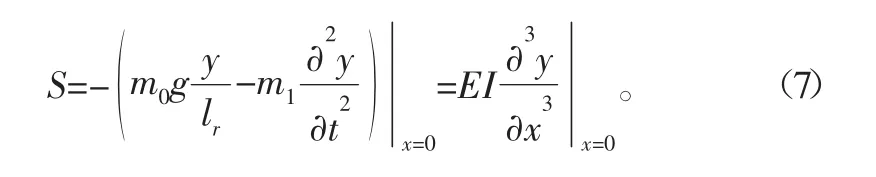
式中：g为重力加速度；m1为顶端质量；m0为总质量；lr为悬挂的绳长，悬绳质量忽略不计。

在方程（7）中，近似为y方向上重力的分力。

在底部（x=l），力矩M为0，剪切力S取决于底部质量的惯性力。此外，顶端和底部各自的剪切力方向是相反的。

力矩：

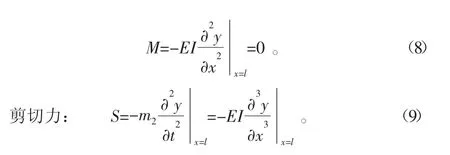
式中：m2为底端质量;l为梁长。

由于任意系数C1、C2、C3、C4不全为零，令C4=1,将方程（6）、（7）、（8）、（9）代入方程（4），得到方程

参数α1,α2,α3和θ的定义如下：

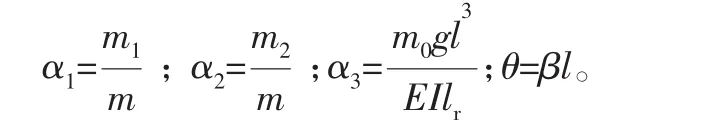
式中：m为梁的质量；α1和α2分别为梁的顶端和底部的质量系数；α3为绳长系数。将方程（10）“[]”中的式子除以2，

令f（θ）=0，得到悬挂梁得固有频率方程，同时，方程（11）可写成如下形式：

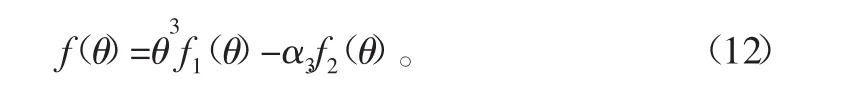
其中，

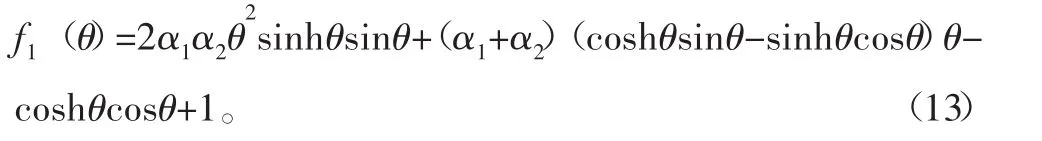
令f1（θ）=0，此为符合下面的边界条件的自由-自由边界条件下的固有频率方程，

在顶端（x=0）

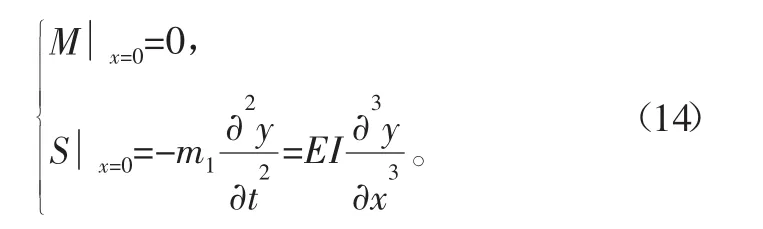
在底部（x=l）

另一面，f2（θ）的定义如下：f2（θ）=2α2θsinhθsinθ+coshθsinθ－sinhθcosθ。令f2（θ）=0，此为符合下面的边界条件的简支-自由边界条件下的固有频率方程：

在顶端（x=0）

在底部（x=l）

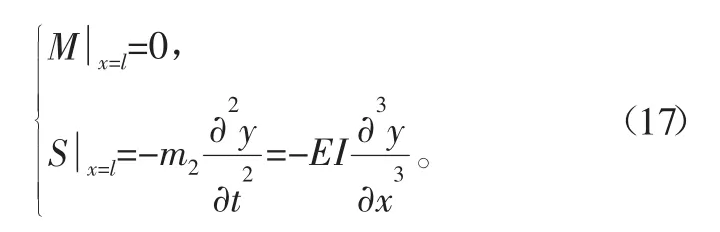
因此，振冲器的振动特性结合了自由-自由和简支-自由条件，所以固有频率也受这两种条件的影响。两种条件的改变程度随悬绳长度变化而变化，随着lr趋于零或α3趋于无穷大，振动特性趋于简单的支撑-自由条件下的振动；lr趋于无穷大或α3趋于零，振动特性趋于自由-自由条件下的振动。

为了研究悬绳长度和底部质量对梁的固有频率的影响，验证上述趋势，实验中悬绳长度和底部质量是变化的，振动频率能被测量出来。梁长与悬绳长的比率变化范围为1.4～140。f2（θ）=0和f1（θ）=0分别对应悬绳最短和最长时的实验结果。

3 ANSYS建模与模态分析

悬梁的模态分析主要是为了确定梁的固有频率。有关ANSYS建模的方法中，可直接建立线性实物模型，然后通过划分网格生成有限元分析模型，也可以直接建立有限元模型，本次的建模采用的是后者[12-15]。梁单元类型采用的是Beam 2 node 188单元，质点单元选用Structural Mass 中3D mass 21单元，如图3、图4分别表示m2=0，固定-自由和自由-自由条件下的位移云图。

4 数据对比分析

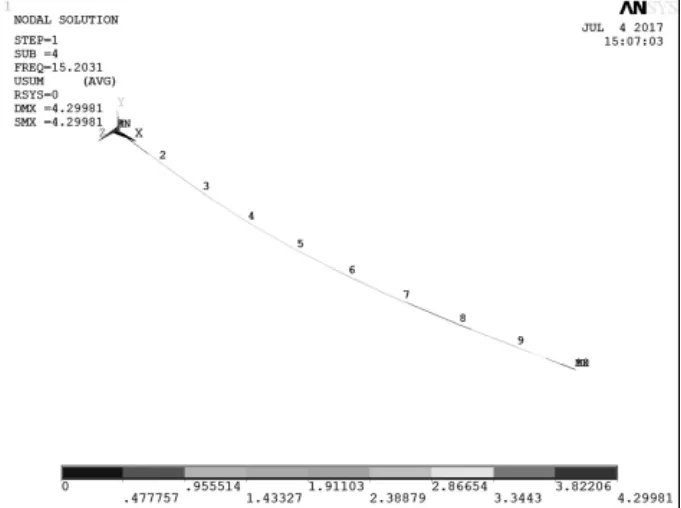
图3 m2=0条件下，固定-自由状态分析云图

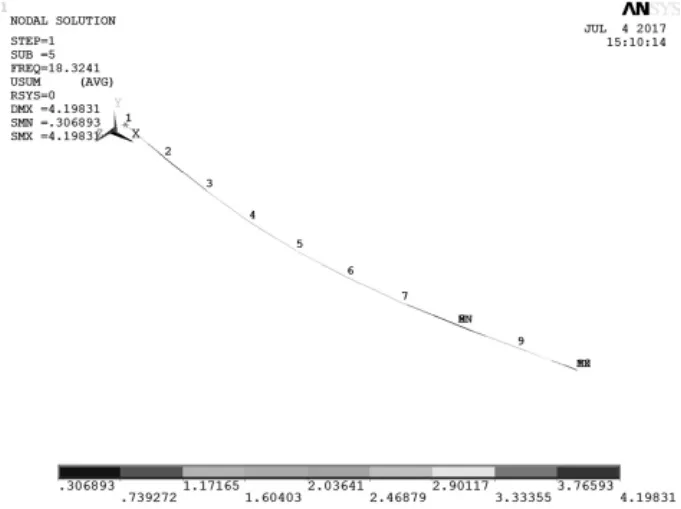
图4 m2=0条件下，自由-自由状态分析云图

本次实验中所选用的梁（E=210 GPa,ρ=7.85×103kg/m3）厚度为2 mm，底部载荷与各系数的关系如表1。表中α3的下标代表绳长，mm。

当梁长与绳长之比为140时，此时绳长为5 mm，通过增大底部载荷，α3的值也越来越大。如图5所示，其中f1-t，f1-e，f1-l，f1-ga分别对应一阶频率的理论分析值，实验测量值，一端铰链一端自由边界条件下的计算值以及固定-自由条件下ANSYS的模态分析值。

而当绳长为500 mm时，此时梁长与绳长的比率为1.4，因为此时的一阶频率均趋于零，故考虑二阶频率，如图6所示，f2-t，f2-e，f2-z，f2-za分别对应二阶频率的理论分析值，实验测量值，自由-自由边界条件下的计算值以及此条件下ANSYS的模态分析值。

对振冲器的振动特性分析中，悬绳长度以及底部载荷对其影响的理论分析模型所计算出的结果与实验结果一致。证实了悬绳长度以及底部载荷对振冲器的影响。

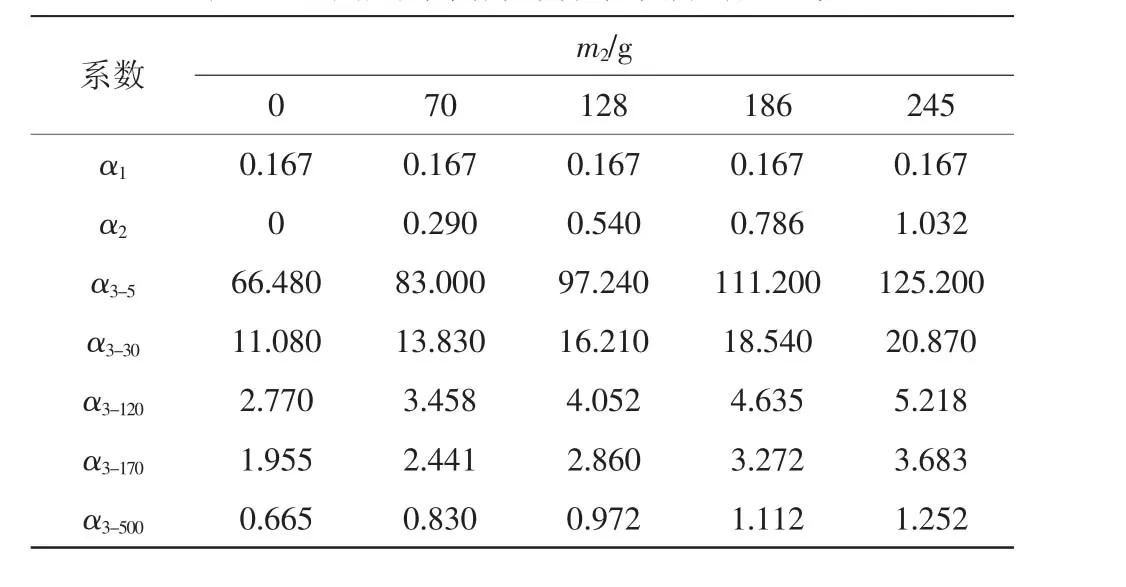
表1 不同底部载荷与各系数所对应的值

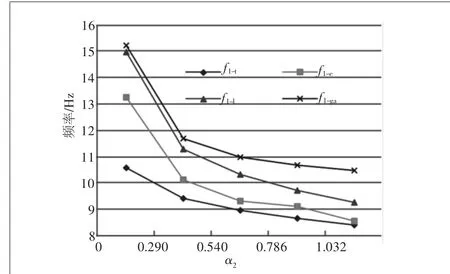
图5 各情况所得一阶频率与α2的关系

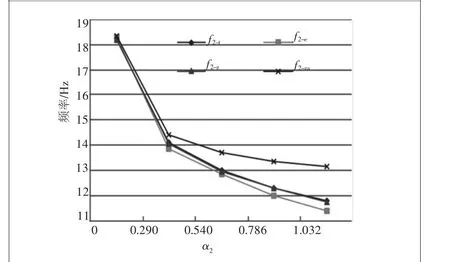
图6 各情况所得二阶频率与α2的关系

悬绳长度以及底部载荷的影响有以下几点：1）底部载荷不变时，随着悬绳长度的增加，一阶固有频率和二阶固有频率均减小。2）当悬绳长度相对较短时，随着振冲器底部载荷的增加，其一阶固有频率减小；反之，当悬绳长度相对较长时，随着振冲器底部载荷的增加，其一阶固有频率增加。而不管悬绳长或短，随着底部载荷增大，二阶频率均减小。3）当悬绳长度很长，α3的值相应很小时，由方程（12）知f1（θ）趋于零，此时的振动特性相似于自由-自由边界条件下的情况。4）当悬绳长度很短，α3的值相应很大时，由方程（12）知f2（θ）趋于零，此时的振动特性相似于简支-自由边界条件下的情况。5）当悬绳长度较短且一定时，随着底部载荷的增大，所得频率的理论值，实验值以及铰链-自由条件下的计算值逐渐接近，而ANSYS所模拟出的固定-自由条件下的结果反而差距更大。说明把固定-自由情况设为边界条件会产生更大的误差。6）当悬绳长度较长且一定时，随着底部载荷的增大，所得的频率差距越来越大，α3对频率的影响也越来越大。