长尾群组推荐的免疫多目标优化实现
2018-06-14韩亚敏柴争义李亚伦朱思峰
韩亚敏, 柴争义,2,, 李亚伦, 朱思峰
(1. 天津工业大学 计算机科学与软件学院,天津 300387; 2. 诺丁汉大学(英国) 计算机学院,诺丁汉 NG8 1BB; 3. 周口师范学院 数学与统计学院,河南 周口 466001)
推荐系统作为解决信息过载的有效方式,在电子购物、新闻阅读、互联网广告等众多领域得到了广泛应用[1].传统推荐算法针对单个用户的设计,无法满足现实中的某些需要,比如聚餐、看电影、旅行等一系列行为通常是以群组的形式发生的,群组推荐将推荐对象由单一用户扩展到多个用户,需要满足多个用户的偏好并对其进行融合.众多学者对其关键问题进行研究.文献[2]研究了认知与社交模型下的群组推荐; 文献[3]基于投票聚合策略与元学习技术,探索群组协作搜索、选择、评价、推荐的方法; 文献[4]利用社区网络结构发现群组,提出一种基于社交网络社区的组推荐框架; 文献[5]采用矩阵分解技术对小、中、大型3种群组进行推荐; 文献[6]对组推荐的研究现状进行了总结和展望.
总之,已有的群组推荐主要集中在如何满足用户偏好,提高推荐的准确度,对推荐的多样性和新颖性方面关注较少[6].众多研究表明,长尾物品同样重要,有利于提高推荐结果的多样性和新颖性[7-8].因此,笔者将长尾物品引入群组推荐,考虑准确度和“长尾”的矛盾性,将其建模为多目标问题,采用免疫优化进行求解.算法旨在满足群组对推荐列表满意度的基础上,提高推荐物品的长尾覆盖率,发挥长尾效益.实验结果表明了算法的有效性.
1 推荐问题建模
1.1 推荐的长尾问题
传统的推荐算法为满足用户的偏好,主要考虑提高推荐的准确度,倾向于推荐一些流行的物品[6].而事实上假使没有推荐系统,用户也很容易通过其他途径获取这些流行度较高的物品,系统价值意义不大.因此,很多研究者致力于长尾,也就是不流行物品的推荐[7-8].很显然,如果仅推荐不流行的物品,将导致准确度很低,对推荐系统来说,同样是没有意义的.一个好的推荐系统应该权衡两者,得到一个较好的均衡解.
另一方面,很多互联网数据研究表明,用户行为符合长尾分布[8].用户经常购买或访问的物品主要集中在长尾的头部,即比较流行的物品.而长尾理论表明,尾部物品的总体效益同样不容小觑.对用户来说,不流行而恰好所需的物品,无疑可以提高用户的惊喜度,让用户获得更加多样与新颖的选择,增加用户与推荐系统的粘合度;而对物品提供商来说,长尾推荐可以提高潜在的收益,对推荐系统的实际应用存在非常重要的价值.因此,在群组推荐中,考虑长尾物品有着理论和实际意义.
1.2 多目标长尾群组推荐建模
推荐问题通常被描述为一个定义在用户空间和物品空间上的效用函数.推荐系统的目的就是把特定的物品推荐给用户,使效用函数最大化[9].
定义函数F(G,i)表示群组G对物品i的效用函数,top-N群组推荐问题为:给定群组G,找到效用函数最大的物品集合R,并满足约束条件R=N.其中N为最终推荐列表的长度.表示如下:
(1)
传统群组推荐主要满足群组中用户的偏好,提高推荐结果的准确度.考虑到推荐的长尾问题,笔者将其建模成多目标问题,一方面保证群组推荐的准确性;另一方面降低推荐结果的流行度,挖掘长尾物品.
设用户u和物品i的相似度记为S(u,i),则群组中用户对推荐结果的满意度定义为
(2)
函数f1计算了群组对推荐列表的平均相似度以衡量推荐的满意度.相似度越高,代表物品越符合用户的偏好.其中,采用余弦相似度计算,公式如下:
(3)
由于长尾物品很少被评分,而流行的物品会受到广泛评价.通常的作法是基于评分数量来判定流行度.但是依靠评分数量对很多评分相同的物品并不合适.最恰当的办法是利用物品评分的均值与方差[10].设物品i的流行度定义为
mi=1μi(σi+1)2,(4)
其中,μi和σi分别代表物品i的评分均值和方差.物品越流行,m值越小.整个推荐列表中物品的流行度为
(5)
为了挖掘更多的长尾物品,函数f2越大越好.同时,为了提高组用户的满意度,也要求函数f1越大越好.显然,这两个目标是相互制约的,推荐流行度高的物品可以提高推荐的准确性和用户满意度,但会降低整个推荐列表的物品流行度,反之亦然.因此,这是一个典型的多目标优化问题.所以,长尾群组推荐的多目标问题可设置为
maxf1(R),f2(R) .(6)
2 长尾群组推荐的免疫多目标优化实现
2.1 算法描述

图1 长尾群组推荐算法流程
2.2 群组数据预处理
群组推荐的数据来源一般包括组成员行为历史、浏览记录、用户-项目评分等[6,11].文中将用户集、物品集、用户-项目评分矩阵作为群组数据来源.表示如下:
(1)U={u1,u2,…,um},m个用户的集合;
(2)I={i1,i2,…,in},n个物品的集合;
(3)D={du,i|u∈U,i∈I},用户对物品的评分数据.
在D中,du,i=0,表示用户u尚未对物品i进行打分.实际中,评分矩阵相当稀疏.矩阵分解的推荐方法能够有效缓解评分数据稀疏问题[12].文中选用的是矩阵分解的一个代表,即奇异值分解,其可以表示为
D=XΣYT=XΣ1/2(YΣ1/2)T,(7)
其中,X,Y是正交矩阵,Σ是对角矩阵.在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了.故通常用前k个奇异值来近似描述矩阵.SVD如下所示:
(8)
由此得到用户特征矩阵M和物品特征矩阵N,即
其中,k是特征空间的维度.矩阵M和N的每一行分别代表对应用户和物品的特征向量.
2.3 群组发现与偏好融合
文中根据用户的偏好动态发现群组.算法随机产生一组用户作为待推荐群组,计算用户之间的相似度;根据用户之间的相似度关系,发现该组用户的代表群组.具体的群组发现过程如算法1所描述.其中,δ为相似度的门限值.
算法1 群组发现.
输入: 随机输入k个用户的集合U
输出:G群组
1. for useri,jfromU&&j≠ido
2.SU[i][j]←cos(U[i],U[j]);
3. end for
4.G←U;
5. for userifromUdo
6. if ∀jfromU&&j≠i,SU[i][j]<δthen
7. G←G-i;
8 end if
9. end for
10. returnG.
群组发现后,重要的一步就是如何对不同用户的偏好进行融合.融合策略有公平策略、均值策略、痛苦避免策略、最小痛苦策略、最开心策略等不同方法[6].文中采用最常用的均值策略进行偏好融合.首先通过用户和物品的特征相似性计算评估该用户对物品的喜爱程度,获取用户的物品偏好序列.取每个用户最喜爱的前r个物品,组成临时物品集.根据不同物品出现的频率对物品集划分阶级,依次加入候选集,直到候选集达到r个; 最后加入的阶级根据均值融合策略作截断处理.具体如算法2所示.
算法2 群组偏好融合.
输入: 群组G,用户特征矩阵M,物品特征矩阵N,候选集大小r
输出: 群组推荐的候选集RC
1.IS←Ø;
2. for userifromGdo
3. for itemjfromIdo
4.SI[i][j]←S(M[i],N[j]);
5. end for
6.Z←Sort(SI[i],descend);
7.IS←IS∪Z[1:r];
8. end for
9.k←1,RC←Ø;
10. whileIS≠Ø
11.F{k}←findCommon(IS); /*返回IS的最频繁子集,并从IS中移除该子集*/
12.RC←RC∪F{k};
13. ifRC>rthen
14.RC←RC-F{i}; break;
15. end if
16.k++;
17. end while
18.IC←sort(F{k},descend);
19.i←1;
20. whileRC 21.RC←RC∪IC[i]; 22.i++; 23. end while 24. returnRC. 免疫智能作为一种仿生学算法,在解决多目标优化问题上取得了很好的效果[13-14].文中对上面生成的组推荐列表,考虑物品的长尾效应,进一步使用免疫算法进行优化,得到用户满意度和物品流行度均衡的推荐结果. 2.4.1 编 码 抗体代表群组推荐中的候选解.每一个候选解都是候选集RC的子集.不同于文献[15],笔者采用实数编码,更易于理解和执行后面的免疫操作.每一个抗体以向量的形式表示一个推荐列表,表示为 X={x1,x2,…,xL} ,(11) 其中,L为推荐列表的长度,满足X=L.每一个xi是RC中的一个元素,并且元素各不相同,保证同一物品在同一推荐列表中不能被推荐2次.迭代中的一组推荐列表形成抗体种群. 2.4.2 亲和力度量 亲和力是抗体的适应性度量,文中长尾群组推荐的多目标是max{f1(R),f2(R)},所以亲和力的度量就是计算max{f1(R),f2(R)}. 2.4.3 交 叉 传统的单点交叉会造成X中的元素重复.对此,文中作了如下变化,如图2所示.x1,x2在6th处单点交叉产生y1,y2.造成y1中3th和9th元素相同,y2中5th和7th元素相同.然后,随机从候选集中选择其他元素进行替换,保证候选解中元素彼此不同. 图2 交叉算子图3 变异算子 2.4.4 变 异 变异算子采用单点变异,从候选集中挑选一个不属于X的元素随机替换xi,形成新的X.如图3所示,概率选择3th元素进行单点变异. 综上,多目标免疫优化具体步骤如下: (1) 初始化生成NM个抗体,即种群P0,设t=0. (2) 计算种群Pt的抗体亲和力.根据帕累托占优,找出其中的占优抗体,记作占优种群Dt.如果Dt≤NM,则Dt+1=Dt;否则,按拥挤距离排序,前NM个抗体组成Dt+1.具体拥挤距离计算详见文献[13]. (3) 如果t≥Gmax,算法结束,输出Dt+1;否则,t=t+1,执行步骤4. (4) 如果Dt≤NA,则活动种群At+1=Dt;否则,按拥挤距离排序,前NA个抗体组成At. (5) 按比例克隆At,组成大小为NC的克隆种群Ct. 群组推荐要求测试数据集包含群组信息,目前在组推荐领域还没有标准的测试集[6].组推荐通常利用传统数据集构建群组或随机生成群组进行实验评价.文中利用经典数据集MovieLens对随机群组作实验.数据集MovieLens是来自 6 040 个用户对 3 952 部电影的 1 000 209 条评分,且所有的评分都是[1,5]之间的整数.实验中,将数据集分成2份,80%作为训练集,20%作为测试集.参数设置及其含义如表1所示. 表1 参数设置 3.2.1 准 确 度 准确度是推荐系统的一个重要指标[16],用来衡量推荐列表中与目标用户相关的物品占比.可表示为 P(R)=R∩TR,(12) 其中,R是系统的推荐列表,T是测试数据集中与用户相关的物品集合.如果用户对某个物品的评分大于等于3,则认为该物品与此用户相关.以群组内用户准确度的均值作为群组的准确度.P(R)值越大,则代表推荐结果的准确度越高. 3.2.2 多 样 性 多样性衡量推荐列表中物品之间的差异性[17].文中使用Jaccard相似系数计算两个项目之间的类型相似度,然后通过计算整个推荐列表之间的相似度来评价推荐结果的多样性.假设A和B代表两个物品,则Jaccard相似系数可以如下表示.值越大,相似度越高. J(A,B)=A∩BA∪B.(13) 则推荐列表R的多样性可以表示为 (14) 其中,J(Ri,Rj)代表物品Ri和Rj之间的类型相似度. 3.2.3 新 颖 性 新颖性是对推荐列表不流行程度的一个评价指标,衡量系统挖掘长尾物品的能力[8,16].其公式为 (15) 其中,pi代表推荐列表中第i个物品的度,是对该物品有评分行为的用户个数.新颖性的值越低,越倾向于推荐不流行的物品,即推荐的物品越处于长尾曲线的尾部. 图4 群组[151,198,2 276,4 921,5 515]的帕累托前沿 文中随机产生大小为2、5、10、20、40的群组,对其进行实验.如图4所示为群组[151,198,2 276,4 921,5 515] 迭代得到的帕累托前沿.横纵坐标分别为衡量组内用户对推荐物品的满意度和推荐列表中物品的流行度.图中的每个点代表一个推荐列表,实验参数NM设置为20,即得到20个推荐列表.从图4可以看出,在一次的迭代过程中,算法产生不同满意度与流行度权重的多个推荐结果.其中,a点(0.129,926.75),x值最小,y值最大,表示点a满意度最低,但物品更处于长尾的尾部; 反之,b点(0.234,101.88),x值最大,y值最小,表示点b满意度最高,但物品更偏向于长尾头部. 算法对2、5、10、20、40等不同组大小的群组推荐结果以准确度、多样性和新颖性进行评价.在一次迭代中,算法为群组产生多个推荐列表,其中,表2以群组[151,198,2 276,4 921,5 515] 的一组推荐列表为例,展示了各成员与群组整体的准确度、多样性、新颖性情况.对于群组中少数用户如 5 515 准确度为0,但大多数用户准确度为 0.2~ 0.3,群组整体的准确度达到0.2.多样性值为0.104,代表物品之间的不相似性高达0.896左右,推荐列表的多样性较好.另外列表的新颖性为241.34,意味着推荐物品在数据集 6 040 个用户基数下平均只有4%的用户对其进行过评价,验证了算法对长尾物品的挖掘能力. 表2 群组准确度、多样性与新颖性情况 图5 不同群组大小的指标对比 文中对考虑长尾物品和不考虑长尾物品的情况作了对比,实验结果如图5所示.结果表明,算法在群组大小为2、5、10、40时,准确度高于非长尾群组推荐,证明长尾群组推荐有效保持了推荐准确度.其中,群组大小为2时,准确度最高;随着成员的增多,准确度有所下降.这是因为成员越多,不同的偏好越难满足,因此,在理论上是合理的.从图5(b)和图5(c)可以看出,算法在组大小为2时,多样性和新颖性优势不明显,但群组大小为5、10、20、40时,多样性与新颖性优于非长尾群组推荐,验证了算法的有效性. 由于群组推荐中,动态生成的群组,成员是动态的,因此,无法与其他算法进行有效比较.与已有的组推荐研究类似,文中仅验证了算法的可行性,相关研究还需进一步探讨. 笔者将考虑长尾效应的群组推荐建模成一个多目标问题,并利用免疫优化算法进行求解,旨在同时优化推荐结果的准确性与推荐物品的流行度.实验结果表明,算法在满足群组满意度的情况下,能提高物品的多样性和新颖性,增加其长尾覆盖率.但是算法在群组较大时,准确度还不是太好,有待以后继续研究. [1] LACERDA A. Multi-objective Ranked Bandits for Recommender Systems[J]. Neurocomputing, 2017, 246: 12-24. [2] QUIJANO-SANCHEZ L, DIAZ-AGUDO B, RECIO-GARCIA J A. Development of a Group Recommender Application in a Social Network[J]. Knowledge-Based Systems, 2014, 71: 72-85. [3] ZAPATA A, MENENDEZ V H, PRIETO M E, et al. Evaluation and Selection of Group Recommendation Strategies for Collaborative Searching of Learning Objects[J]. International Journal of Human-Computer Studies, 2015, 76: 22-39. [4] 刘宇, 吴斌, 曾雪琳, 等. 一种基于社交网络社区的组推荐框架[J]. 电子与信息学报, 2016, 38(9): 2150-2157. LIU Yu, WU Bin, ZENG Xuelin, et al. A Group Recommendation Framework Based on Social Network Community[J]. Journal of Electronics & Information Technology, 2016, 38(9): 2150-2157. [5] ORTEGA F, HERNANDO A, BOBADILLA J, et al. RecommendingItems to Group of Users Using Matrix Factorization Based Collaborative Filtering[J]. Information Sciences, 2016, 345: 313-324. [6] 张玉洁, 杜雨露, 孟祥武. 组推荐系统及其应用研究[J]. 计算机学报, 2016, 39(4): 745-764. ZHANG Yujie, DU Yulu, MENG Xiangwu. Reserch on Group Recommender Systerms and Their Applications[J]. Chinese Journal of Computers, 2016, 39(4): 745-764. [7] VALCARCE D, PARAPAR J, BARREIRO A. Item-basedRelevance Modelling of Recommendations for Getting Rid of Long Tail Products[J]. Knowledge-Based Systems, 2016, 103: 41-51. [8] WANG S F, GONG M G, LI H L, et al. Multi-objective Optimization for Long Tail Recommendation[J]. Knowledge-Based Systems, 2016, 104: 145-155. [9] QUIJANO-SANCHEZ L, SAUER C, RECIO-GARCIA J A, et al. MakeIt Personal: a Social Explanation System Applied to Group Recommendations[J]. Expert Systems with Applications, 2017, 76: 36-48. [10] PARK Y J. The Adaptive Clustering Method for the Long Tail Problem of Recommender Systems[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(8): 1904-1915. [11] FENG S S, CAO J. Improving Group Recommendations via Detecting Comprehensive Correlative Information[J]. Multimedia Tools and Applications, 2017, 76(1): 1355-1377. [12] FANG Y N, GUO Y F. A Context-aware Matrix Factorization Recommender Algorithm[C]//Proceedings of the 2013 IEEE International Conference on Software Engineering and Service Science. Washington: IEEE Computer Society, 2013: 914-918. [13] 雷雨, 焦李成, 公茂果, 等. 求解多目标考试时间表问题的NNIA改进算法[J]. 西安电子科技大学学报, 2016, 43(2): 157-161. LEI Yu, JIAO Licheng, GONG Maoguo, et al. Enhanced NNIA forMulti-objective Examination Timetabling Problems[J]. Journal of Xidian University, 2016, 43(2): 157-161. [14] CHAI Z Y, YAN X Y, LI Y L, et al. Throughput Optimization in Cognitive Wireless Network Based on Clone Selection Algorithm[J]. Computer and Electronic Engineering, 2016, 52: 328-336. [15] GENG B R, LI L L, JIAO L C, et al. NNIA-RS: a Multi-objective Optimization Based Recommender System[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 424: 383-397. [16] ZUO Y, GONG M G, ZENG J L, et al. Personalized Recommendation Based on Evolutionary Multi-objective Optimization[J]. IEEE Computational Intelligence Magazine, 2015, 10(1): 52-62. [17] KUNAVER M, POZRL T. Diversity in Recommender Systems—a Survey[J]. Knowledge-Based Systems, 2017, 123: 154-162.2.4 多目标免疫优化推荐

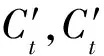
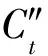
3 实验评估
3.1 数据集与参数设置

3.2 评价指标
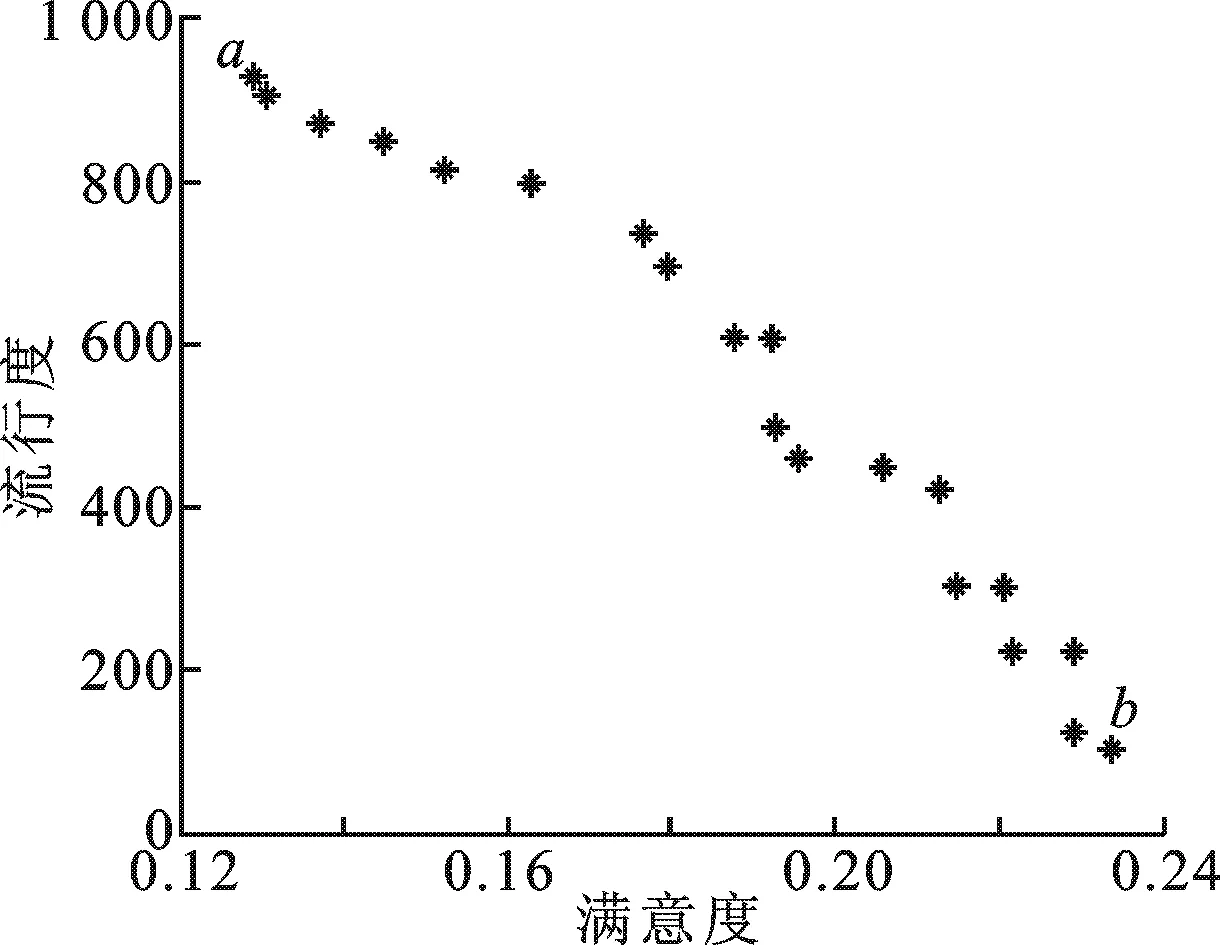
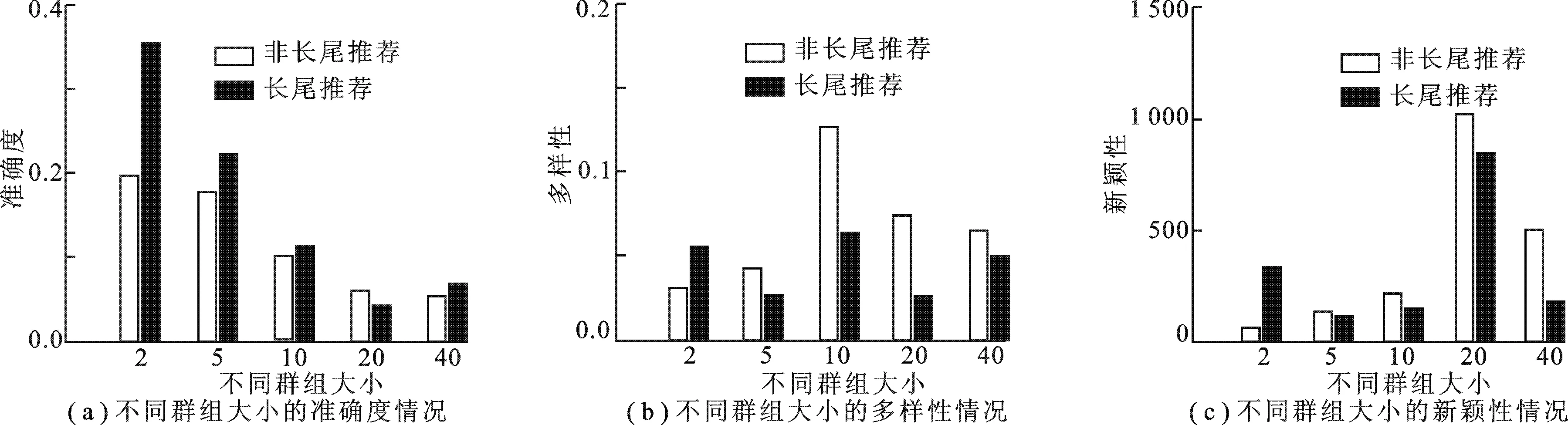
3.3 实验结果

4 结 束 语
