多尺度方法预测复合材料层板裂纹扩展

储辰辰， 蔡 恒， 乔晓军， 叶俊杰

(1. 西安电子科技大学 应用力学研究中心，陕西 西安 710071；2. 太原重工股份有限公司技术中心，山西 太原 030024)

复合材料具有比强度高、比模量大、抗疲劳性能好和破损安全性能高等多种优良特性，被应用在航空、风力发电和建筑等领域．由于材料损伤破坏引起的安全事故时有发生，对复合材料的损伤机理研究也变得尤为重要．目前复合材料性能失效分析方法包括宏观力学分析法和多尺度分析法．许多学者使用了宏观的力学方法研究复合材料的损伤失效行为．文献[1]采用了改进的三维Hashin准则建立了复合材料低速冲击渐进损伤模型，计算了冲击载荷下层板的层内和层间分层损伤结果．文献[2]基于连续损伤力学方法研究了编织材料在不同应变率下的渐进损伤模型．使用宏观力学研究方法计算效率高，但是宏观的失效准则是经验的，宏观材料的属性是不确定的，宏观材料参数与层板的铺层构造和纤维的体积含量等因素有关．宏观上的损伤都是由细观损伤扩展、积累而来的，所以使用多尺度方法研究复合材料的失效状态更为合理和科学．文献[3]对应变硬化复合材料多尺度建模，使用晶格模型研究了裂纹行为对纤维分散体的敏感性．文献[4]使用了基于通用单胞模型的多尺度方法研究了纤维增强型复合材料的初始和最终表面失效．文献[5]使用了基于多尺度方法的复合材料单胞力学模型，预测了纤维织物增强柔性复合材料的拉伸模量．文献[6]使用了多尺度方法，结合了多轴强度准则和细观材料退化，研究了螺栓连接的复合材料层板的渐进失效分析．

然而将多尺度方法应用于材料结构宏观裂纹扩展的研究较少．文中采用高精度通用单胞模型理论建立细观力学模型，结合商业有限元软件LS-DYNA对复合材料层合板进行多尺度建模．使用最大应力准则判断细观损伤模式，并将失效组分材料参数退化．同时定量给出组分性能失效对宏观单层板的影响，使用具有归一化指标来量化宏观刚度损伤时的比例值来确定宏观的损伤，宏观的单元一旦损伤即不再承受载荷，以此模拟裂纹扩展．

1 细观力学模型

高精度通用单胞模型是由文献[7]提出的一种分析具有周期性细观结构特点的复合材料细观力学模型发展而来的．如图1所示，纤维增强型复合材料具有宏观上的均匀性在细观上周期性的特点，并且纤维在轴向方向上是无限延长的，所以可将这类复合材料力学行为研究简化到二维方向来处理．利用纤维排列的周期特性确定一个最小的重复单元，可以认为重复单胞的力学性能就是材料的力学性能．通用单胞模型理论基本思想是: 重复单胞的尺寸是h×l(如图2所示)，将这种重复单胞分成Nβ×Nγ个的矩形子胞，每个子胞可以赋予不同的材料．

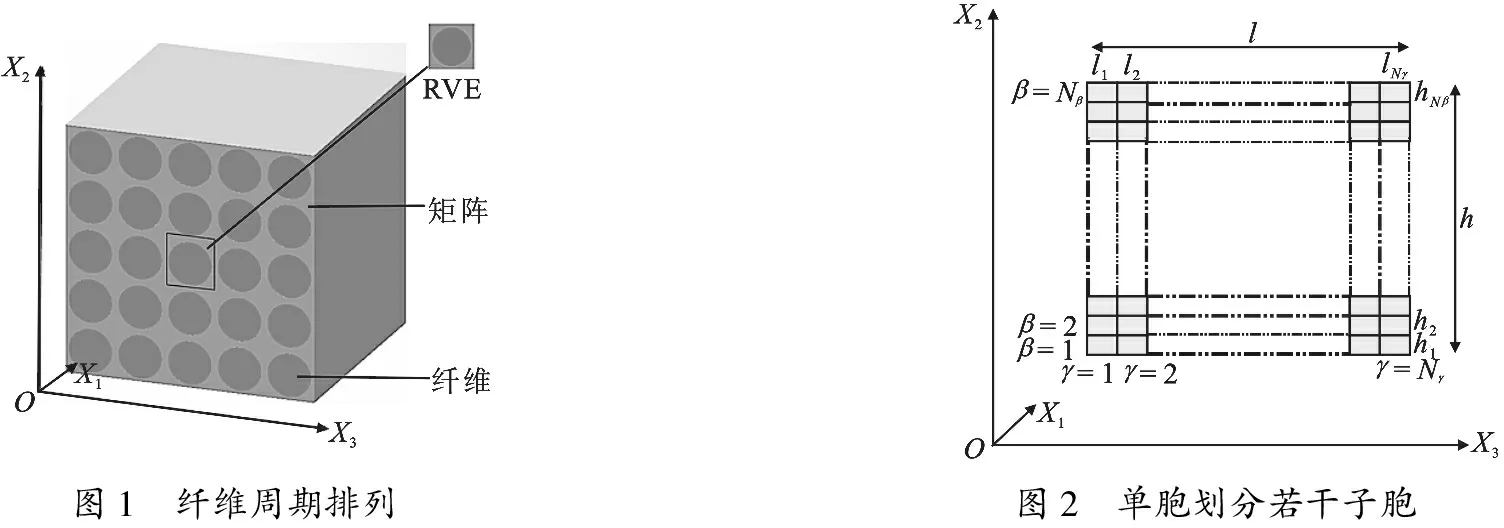
图1 纤维周期排列图2 单胞划分若干子胞

子胞位移与宏观应变满足下列关系:

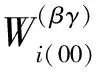
相邻子胞满足位移和应力连续条件:

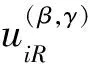
在高精度通用单胞模型理论中，研究宏观材料拉伸条件下的非线性行为主要是研究组分材料的非弹性即重复单胞中的每一个子胞材料的非弹性．子胞的平均应力应变可采用子胞中的本构方程来表达．子胞的平均应力的表达式为

(6)

通过联立式(1)～(6)，可以建立子胞的平均应变和应力与宏观应变和应力之间的关系，即

2 多尺度损伤分析方法

复合材料结构损伤从材料内部损伤开始萌发，内部损伤的积累引起层板的失效，最终导致结构的失效．宏观结构的损伤本质上是细观上组分材料的失效引起的．

文中使用的高精度单胞模型细观力学方法结合细观失效准则，研究了复合材料非线性力学行为以及材料内部的损伤; 同时，定量组分失效对层合板宏观性能的影响，并以此作为宏观损伤的判据．

2.1 细观组分材料的失效准则

细观损伤是由子单胞模型中子胞的应力以及相应材料的强度值所控制．文中使用最大应力准则公式计算子胞的损伤值．当子胞主应力任何一个方向的应力达到单轴拉伸、压缩和剪切强度时，就代表了子胞材料发生了相应的失效模式，可表示如下：

其中，XT和XC分别是子胞材料的纵向拉伸强度和纵向压缩强度，下标T表示拉伸，下标C表示压缩;YT和YC分别是子胞材料横向拉伸强度和压缩强度;S是子胞材料的剪切强度;D(β γ)描述子胞的损伤严重程度．当D(β γ)=0 时，子胞材料完好; 当D(β γ)=1 时，子胞发生了相应的失效模式．

2.2 子胞材料刚度退化

当子胞材料失效时，需要将损伤的子胞材料刚度退化．由于细观组分中聚合物基体是各项相同性材料，纤维是横观各向同性材料，所以需要考虑5个刚度参数的退化．当组分满足最大应力准则时，则对应的子胞就会失效，可将子胞的刚度分量乘以一个小的系数(0.001)[9]，近似地表达该子胞将不再受载．

2.3 细观损伤积累

由于纤维和基体材料损伤积累到一定的量导致了单胞的最终失效，所以使用参数U来定量描述损伤积累的过程，即

(15)

其中，S0和S分别是子胞材料的初始柔度矩阵和当前柔度矩阵．理论上讲，随着子胞逐渐发生破坏，当U的值接近于零时，单胞也就是单元的积分点不再承受载荷即单元失效．但是由于单胞材料的刚度降低，会使数值计算不容易收敛．为了改进数值求解计算收敛困难的情况，在这里认为当U≤0.5 时，单元失效[10]．

2.4 多尺度损伤分析实现过程

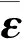
(1) 建立有限元模型施加边界条件、载荷条件．

(2) 有限单元积分点调用细观力学模型，将积分点的应变作为单胞的边界条件求解子胞应力．

(3) 使用细观失效准则判断子胞材料是否失效．若失效，则子胞的材料退化．使用均匀理论计算单胞的应力．

(4) 判断积分点失效．若积分点失效，则单元的刚度乘以1×10-6．

(5) 判断加载是否结束．若没有结束，则重复第2步．

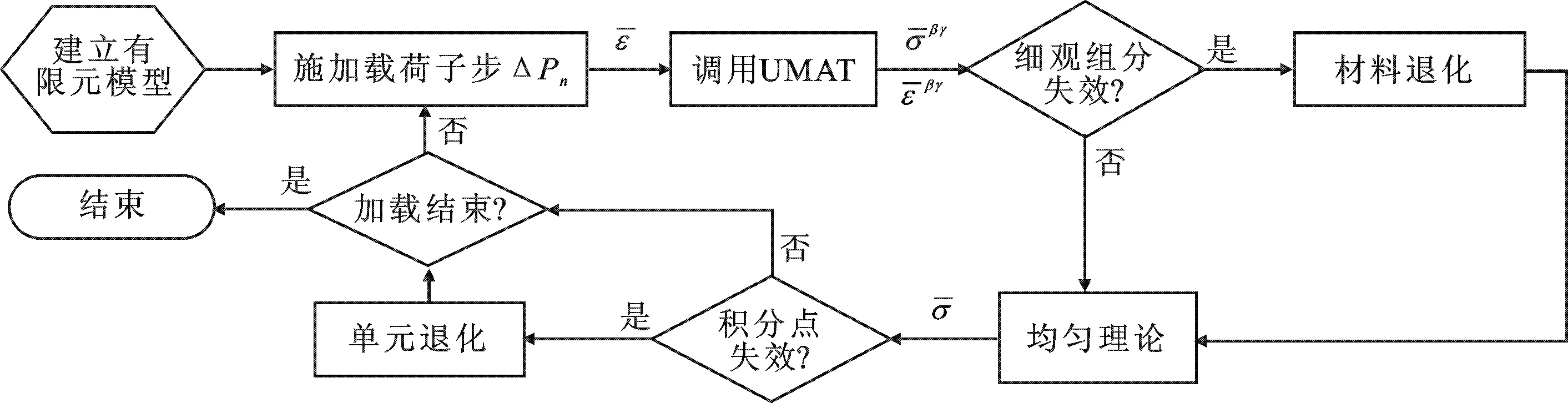
图3 多尺度损伤分析流程图

3 试验结果与数值分析

3.1 开孔层板静力拉伸试验

文中使用的玻璃纤维环氧树脂基复合材料层板，长为200 mm，宽为40 mm，厚为2.4 mm，铺层方向为 [-45°/ 0°/ 45°/ 90°]2，层合板的中心开直径为 12 mm 孔．应变片的位置如图4(a)所示，两应变片垂直距离为 1 cm．层板两端夹持，拉伸速度为 1.5 mm/min．实验使用NI9219模块采集静力拉伸时的应变片的应变值，材料的拉伸试验以及测量记录系统如图4(c)所示．

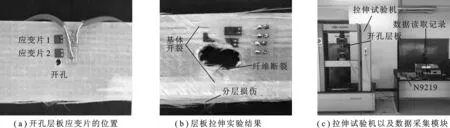
图4 开孔层板静力拉伸试验

3.2 开孔层板的有限元模型

在ANSYS-LSDYNA建立层板的有限元模型．由于铺层对称，厚度方向只采用实际模型的 1/2 铺层．使用shell163单元模拟复合材料层板;结构包含 12 800 单元，模型的左端固定右端施加位移载荷．复合材料由玻璃纤维和基体组成．纤维材料参数: 弹性模量Ef= 71.42 GPa，剪切模量Gf= 30.2 GPa，泊松比νf=0.2; 基体的材料参数: 弹性模量Em= 3.3 GPa， 泊松比νm= 0.22．组分材料的强度值如下: 纤维纵向拉伸强度XT= 1 617 MPa，纵向压缩强度XC= 421 MPa，基体拉伸强度和压缩强度分别是YT= 37 MPa，YC= 121 MPa，剪切强度S= 22 MPa．基体材料的6个塑性相关的参数[11]见表1．

表1 聚合物非弹性本构模型参数

图5是应变片位置1处和位置2处的单元拉伸中的应力计算值与实验值比较．在应变片1处，当总应变达到0.44%时，应力的理论与实验值的最大相对误差为2.93%; 当总应变达到0.899%时，单元失效，此时应力理论结果与实验结果分别是 29.49 MPa 和 29.56 MPa，相对误差为0.23%．在应变片2处，当总应变达到0.35%时，应力的理论与实验值的误差最大为2.93%，由于未考虑分层损伤模型预测层合板的破坏强度和破坏位移，理论值较低于实验值．

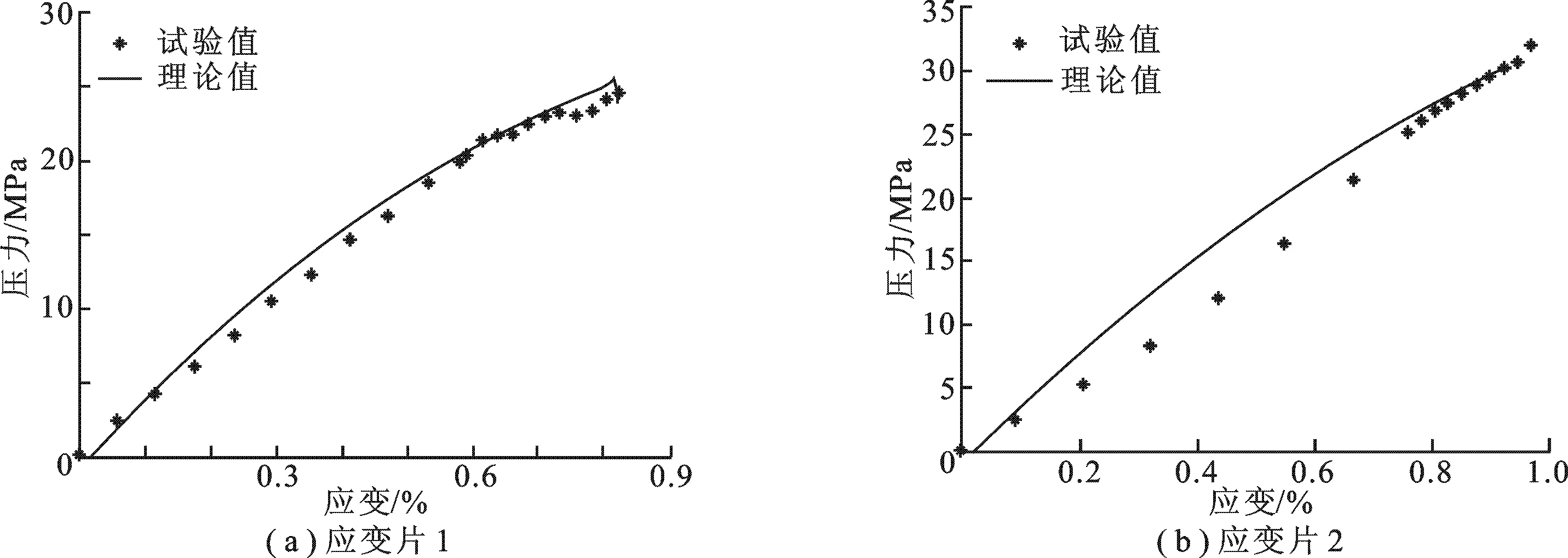
图5 试验值与理论计算值的比较

3.3 细观损伤分析

为了清晰地观察损伤分布，截取了孔周围的部分．图6(a)～(d)是各个层在不同的层板总应变下的基体失效分布，发现0°、45°、-45° 和90°层分别在层板总应变达到 3 573μ ε，3 796μ ε，3 732μ ε 和 3 463μ ε(单位μ ε为微应变)时，基体发生损伤．图6(e)是0°层在层板总应变分别为 5 856μ ε，6 972μ ε，7 865μ ε 下纤维的失效分布图，当层板总应变达到 5 856μ ε 时，首先在0°层板发生纤维失效，纤维失效主要发生在0°层板．图6(a)是0°层的基体失效分布图，失效首先发生在孔沿轴线方向的两侧;由于应力集中的影响，失效又沿着轴向发展; 此外由于纤维承载了主要的应力，所以降低了轴线方向基体的失效扩展．图6(b)和图6(c)是 ±45° 层板的基体失效分布图，同时受铺层角度和应力集中的影响，失效区域沿着铺层角方向以与90°方向呈扇形的区域扩展．图6(e)是0°层板纤维失效分布图，纤维的失效是沿着90°方向向孔的两侧扩展的．

3.4 裂纹扩展分析

图7(a)～(d)是-45°、0°、45°和90°层板的应力云图和裂纹扩展分布图．由于应力集中影响，孔的周围单元，首先出现裂纹; 图7(a)是层板的表面层，裂纹是由纤维束方向基体失效主导引起的，因为纤维的强度远大于基体的强度，裂纹沿着纤维的铺设角度的方向呈扇形扩展．图7(b)发现0°铺层并没有出现裂纹，由于0°铺层的纤维承载了主要的力，并没有引起基体大规模失效．并且外部施加的载荷并没有使整个纤维束失效，从细观损伤分析图发现，纤维子胞是有损伤的，但是损伤没有累积到引起宏观单元失效．图7(c)的裂纹是由基体开裂引起的，由于对称铺层消除了面内面外载荷/变形的耦合，同时存在层间剪切应力的影响，破坏区域没有第1层大．图6和图7揭示了复合材料拉伸载荷下的损伤机理: 复合材料在受拉伸载荷作用时，由于基体刚度较小，在同样变形条件下基体先开裂．随着加载的继续，这种微裂纹在基体中逐渐扩展，汇合成较大的裂纹．当载荷较小的时候，裂纹的扩展受到纤维的抑制，仅在基体内扩展；当裂纹达到一定长度时，剪切失效，导致裂纹沿着纤维方向扩展．基体开裂削弱了纤维和基体的联系，纤维无法再由基体传力，发生断裂，断裂纤维附近应力重新分布，导致断裂纤维周围产生应力集中，加速了纤维的断裂，最终导致复合材料整体快速断裂．

4 结 束 语

文中使用高精度通用单胞细观力学模型建立复合材料宏观单层板与细观组分材料的关系，结合细观损伤准则和宏观损伤判定方法，发展了一种研究复合材料结构细观尺度损伤和预测宏观尺度裂纹扩展的方法．

文中使用了这种方法研究了[-45°/0°/45°/90°]2层板拉伸条件下各分层细观组分损伤，预测了各个分层的裂纹扩展．研究表明，细观上纤维损伤主要发生在0°层，损伤扩展方向垂直于铺层方向; 基体损伤对宏观的裂纹扩展起主要影响．仿真结果表明，各个层板的裂纹沿着纤维角度呈扇形区域扩展，与实验现象符合．同时将计算结果与试验中应变片测量的结果相比较，吻合良好．

[1] 刘万雷, 常新龙, 张晓军, 等. 基于改进Hashin准则的复合材料低速冲击损伤研究[J]. 振动与冲击, 2016,(12): 209-214.

LIU Wanglei, CHANG Xinlong, ZHANG Xiaojun, et al. Low-velocity Impact Analysis of Composite Plates Based on Modified Hashin Criterion [J]. Journal of Vibration and Shock, 2016,(12): 209-214.

[2] BELINGARDI G, MEHDIPOUR H, MANGINO E, et al. Progressive Damage Analysis of a Rate-dependent Hybrid Composite Beam[J]. Composite Structures, 2016, 154: 433-442.

[3] KANG J, BOLANDER J E. Multiscale Modeling of Strain-hardening Cementitious Composites[J]. Mechanics Research Communications, 2016, 78: 47-54.

[4] YE J, QIU Y, CHEN X, et al. Initial and Final Failure Strength Analysis of Composites Based on a Micromechanical Method[J]. Composite Structures, 2015, 125: 328-335.

[5] 李力, 赵海涛, 陈吉安, 等. 基于多尺度方法的纤维织物增强柔性复合材料拉伸模量预测[J]. 复合材料学报, 2016, 33(10): 2312-2318.

LI Li, ZHAO Haitao, CHEN Ji’an, et al. Tensile Modulus Prediction on Fiber Fabric Reinforced Flexible Composite Based on Multi-dimension Method [J]. Acta Materiae Compositae Sinica, 2016, 33(10): 2312-2318.

[6] NERILLI F, VAIRO G. Progressive Damage in Composite Bolted Joints via a Computational Micromechanical Approach[J]. Composites Part B: Engineering, 2017, 111: 357-371.

[7] BEDNARCYK B A, ABOUDI J, ARNOLD S M. Analysis of Fiber Clustering in Composite Materials Using High-fidelity Multiscale Micromechanics[J]. International Journal of Solids and Structures, 2015, 69/70: 311-327.

[8] ABOUDI J, ARNOLD S M, BEDNARCYK B A. Micromechanics of Composite Materials: a Generalized Multiscale Analysis Approach [M]. Oxford: Butterworth-Heinemann, 2012: 53.

[9] 方国东. 三维四向碳/环氧编织复合材料积累损伤及失效分析[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[10] 翟智. 多尺度嵌套细化方法及其在复合材料结构健康监测的应用 [D]. 西安: 西安交通大学，2014.

[11] 叶俊杰. 基于单胞模型的纤维增强复合材料细观力学性能研究及应用 [D]. 西安: 西安交通大学，2011.