具耐药性的乙肝模型研究
2018-06-13郭林娜宋运娜
郭林娜,宋运娜
(齐齐哈尔医学院 基础医学院,齐齐哈尔 161006)
据世界卫生组织报道,乙型肝炎是一种世界性的疾病.乙型肝炎是由乙肝病毒(Hepatitis B Virus, HBV)造成的可能威胁生命的肝脏感染.它是一个严重的全球卫生问题,可造成慢性感染,导致患者死于肝硬化和肝癌的风险很高.亚马逊和中东欧南部地区,估计有2%~5%的人口为慢性感染.西欧和北美有不到1%的人口为慢性感染[1].
我国计生委疾病预防控制局2016年1月(针对2016年1月1日0时至1月31日24时)发布疫情概况,甲乙类传染病合计发病265465例,其中乙型肝炎感染89699例占34%,死亡40例占3.3%[2],乙型肝炎是我国发病率最高的一种传染病.卫生部发布2011—2014年全国乙型病毒性肝炎防治规划推算: 全国有6.9亿人曾感染过乙肝病毒,其中1.2亿人长期携带乙肝病毒,据专家估计,目前中国现有患慢性乙肝的病人达2000万人.乙型肝炎只能采用药物治疗[3],其中干扰素治疗不产生耐药性、血清转换率高且应答持久,具有调节免疫和抗病毒双重功效,但是费用高、不良反应多、部分患者禁忌.患者多采用核苷(酸)类药物,具有“有效性、易行性、安全性”,但是存在疗程不固定、易发生病毒耐药、停药后易复发等的缺点.治疗乙肝疾病成功与否的关键问题就是在用药上,药物疗效的发挥是乙肝疾病防控的关键问题.
对于乙肝这样的传染性疾病,采用试验研究成本太高,而且很多组织认为这样的研究并不人道,科学家们多采用数学模型和数值模拟仿真进行定量研究.很多学者已经做了大量的研究.
Wang等[4]研究了带有病毒性淋巴细胞(Cytotoxic Lymphocyte, CTL)的免疫细胞和非线性发生率的乙肝病毒扩散模型,在模型中引入了拉普拉斯算子和扩散系数,运用Lyapunov函数研究模型的全局渐近稳定性,给出了基本再生数,通过再生数与1之间的比较,判断模型的稳定性.Wang等[5]研究了伴随免疫反应的带时滞微分方程的乙肝模型的全局稳定性,讨论了对病毒敏感CTL细胞的平衡点和对病毒不敏感CTL细胞的平衡点.Shen等[6]讨论了发生在中国的丙型肝炎病毒(Hepatitis C Virus, HCV)传染病的全局稳定性,将急性感染者(传染率最强)、慢性感染者和被治疗的感染者(传染率最低)传染率分别记为β1,β2,β3得到基本再生数,讨论了平衡点的稳定性.Zhang等[7]在乙肝模型中引入了年龄结构的概念,将易感染者分为新生儿、孩子(年龄在1~16岁)、成年人(年龄大于16岁)3个年龄结构,每个年龄结构的人又分为: 易感染者、急性感染者、慢性感染者、治愈者,讨论了复杂模型的平衡点.Zhou等[8]将健康教育和治疗的参数引入到肺结核模型中.罗丽丽等[9]研究了乙肝疫苗接种后体液免疫应答的数学模型.Cheng等[10]考虑了乙肝疫苗不完全起到免疫作用时的乙肝病毒感染数学模型,并分析模型平衡点的稳定性.Khalid等[11]研究了扩散和双时滞混合的乙肝病毒模型,Wang等[12]将分步时滞和多状态的传染病模型引入,研究平衡点的稳定性.Ciupe等[13]着重研究在HBV感染中抗体反应时对应的模型.
为了研究药物在体内的疗效对乙型肝炎疾病发展防控的重要影响,建立模型并进行下面假设:
1) 考虑部分新生儿遗传有天生的抗体,没有考虑垂直传染,因为母婴切断传染技术比较成熟,可以通过拒绝母乳、注射免疫球蛋白等实现;
2) 潜伏者不具有传染性;
3) 慢性乙肝可以由急性乙肝或由无症状乙肝病毒携带者转化来;
4) 人们患上慢性乙肝很难治愈,设敏感性和具有耐药性的慢性乙肝患者的治愈率为零.
1 建立模型

(1)
2 模型的不变区域和非负性
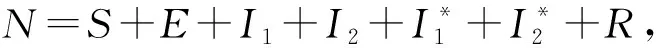
(2)
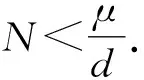
在模型(1)中的R在其他方程中没有出现,将模型(1)简化为下面情形:
(3)
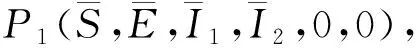
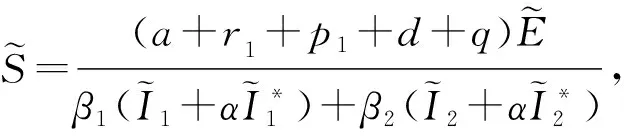
由模型(3)的第1个方程,解得:
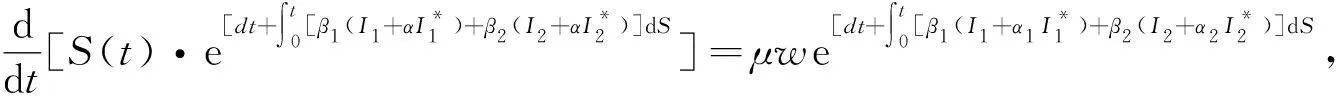
3 无病平衡点的稳定性
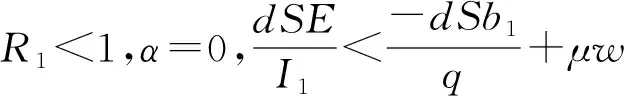
证 根据模型(3)得到2个矩阵:
不考虑具有耐药性病人和敏感病人传染率的差异α=0,谱半径为:
定义Lyapunov函数F1=d(d+d1)(p2+d+r2+b1)E+μwβ2qI1+μwβ1aI2,则
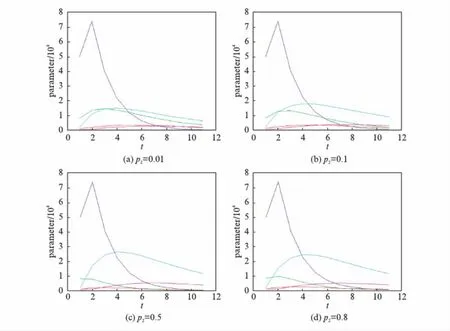
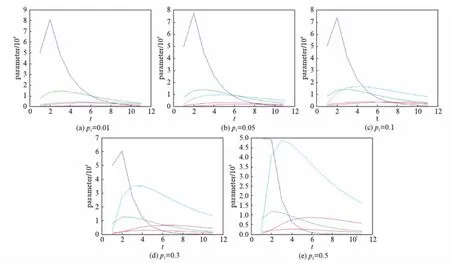
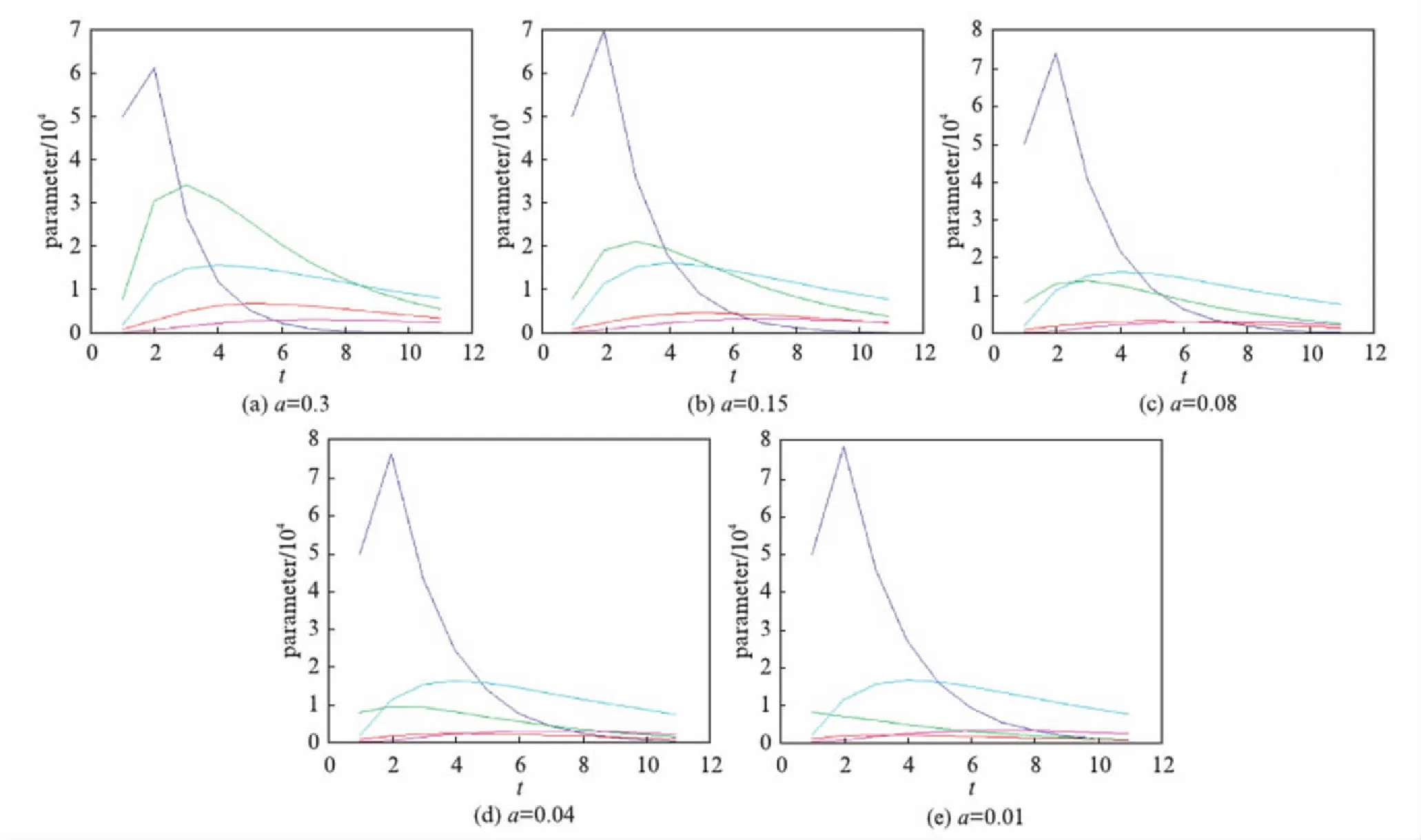
在现实生活中定是乙肝的潜伏者多于患者,所以模型定有E d(d+d1)(p2+d+r2+b1)(β1SI1+β2SI2)-μwβ1a(b1I1+qE)-μwβ2qaE= Ed(d+d1)(p2+d+r2+b1)(a+p1+r1+d+q)(R1-1)-μwβ1a(b1I1+qE)-μwβ2qaE+ d(d+d1)(p2+d+r2+b1)(β1SI1+β2SI2). (4) (5) 证 根据模型(4)得到2个矩阵: F2=(d+d1)(d+r1+b1)E+[β1(d+d1)+β2b1]I1+β2(d+r1+b1)I2, 从而 进一步整理得: (6) (7) 引理1[15]设方程 (8) 证 由模型(6)得到约当矩阵为: 相应的二阶导数复合矩阵为: 令 其中: 设ψ(B)≤sup{g1,g2},其中: 当M1 设某地区慢性乙肝患者约1200万,每10万人口约有0.12万人患有慢性乙肝疾病.根据全国平均发病率935.8人/万人,平均患有慢性乙肝患者为1200人/万人[16].设置初始值: 图的图像 设置相应参数:μ=0.029,ω=0.8,d=0.02,d1=0.333,d2=0.4,q=0.005,b1=b2=0.1,a=0.8,p1=0.1,p2=0.05,β1=0.06,β2=0.038,r1=0.4,r2=0.1. 具有耐药性的HBV疾病在现实生活中多有存在,具有耐药性的HBV疾病是HBV疾病防控的主要方向.从理论上分析,通过控制参数p1,p2的数值,减小敏感性感染初期患者转换为潜伏者的比率a的取值.具体做法: 尽量阻断具有耐药性的传染源、合理规范用药,避免耐药性的产生;尽快研发出有效的药物,通过药物治疗的手段减少HBV疾病的蔓延. 图2 随着参数p2取值的变化,种群的变化图像Fig.2 The population change image with the change of parameter p2 values 图3 随着参数p1取值的变化,种群变化的图像Fig.3 The population change image with the change of parameter p1 values 图4 随着参数a取值的变化,种群变化的图像Fig.4 The population change image with the change of parameter a values 参考文献: [1] WHO. Hepatitis B [EB/OL]. (2015-08-05).http:∥www.who.int/mediacentre/factsheets/fs204/zh/(revised August 2015). [2] 国家卫生计生委疾病预防控制局.2016年1月全国法定传染病疫情概况 [EB/OL].(2016-02-03).http:∥www.nhfpc.gov.cn/jkj/s3578/201602/ceaf73add1924a80bcf134d94d00315c.shtml. [3] 360百科.乙肝抗病毒治疗药物 [EB/OL].http:∥baike.so.com/doc/5377275-5613405.html. [4] WANG S L, FENG X L, HE Y N. Global asymptotical properties for a diffused HBV infection model with CTL immune response and nonlinear incidence [J].ActaMathematicaScientia, 2011,31(5): 1959-1967. [5] WANG J L, TIAN X X. Global stability of a delay differential equation of hepatitis B virus infection with immune [J].ElectronicJournalofDifferentialEquations, 2013,94: 1-11. [6] SHEN M W, XIAO Y N, ZHOU W K.Global dynamics and applications of an epidemiological model for hepatitis C virus transmission in China [J].DiscreteDynamicsinNatureandSociety, 2015(6): 1-13. [7] ZHANG S X, ZHOU Y C. Dynamic analysis of a hepatitis B model with three-age-classes [J].CommumNonlinearSciNumerSimulate, 2014,19(7): 2466-2478. [8] ZHOU X Y, SHI X Y, CHENG H D. Modelling and stability analysis for a tuberculosis model with healthy education and treatment [J].CompApplMath, 2013,32(2): 245-260. [9] 罗丽丽,孟改利,翼贞浩.乙肝疫苗接种后体液免疫应答的数学模型 [J].数学的实践与认识,2011,41(15): 1-11. [10] CHENG Y, PAN Q H, HE M F. Stability analysis of hepatitis B virus model with incomplete immunization of Hep B vaccine [J].AbstractandAppliedAnalysis, 2014(2): 1-10. [11] KHALID H, NOURA Y. A generalized HBV model with diffusion and two delays [J].CompuersandMathematicswithApplications, 2015,69(1): 31-40. [12] WANG J L, LIU S Q. The stability analysis of a general viral infection model with distributed delays and multi-staged infected progression [J].CommunNonlinearSciNumerSimulate, 2015,20(1): 263-272. [13] CIUPE S M, RIBEIRO R M, PERELSON A.Antibody responses during hepatitis B viral infection [J].ComputationalBiology, 2014,10(7): 1-17. [14] 庞建华.具有一个回复率的传染病模型及乙肝数学模型的研究[D].南京: 南京师范大学,2012. [15] SHARMA S, SAMANTA G P. Dynamical behaviour of an HIV/AIDS epidemic model [J].DifferentialEquations&DynamicalSystems, 2014,22(4): 369-395. [16] 张焜和.乙肝病毒感染的基础与临床 [M].南昌: 江西科学技术出版社,1999.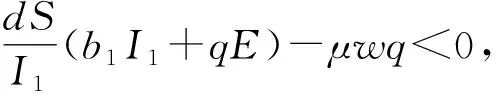
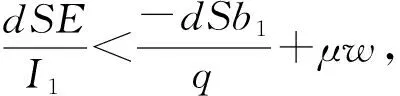
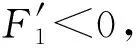
4 无耐药性的边界平衡点的稳定性
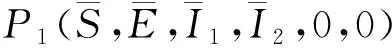
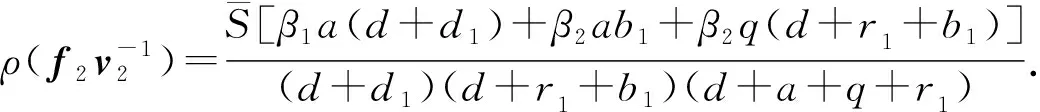
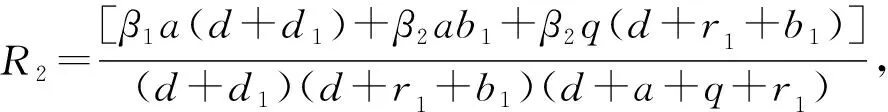
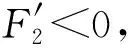
5 具有耐药性的地方病平衡点的稳定性
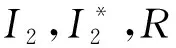
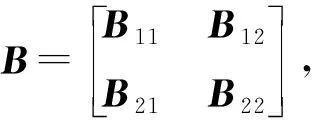
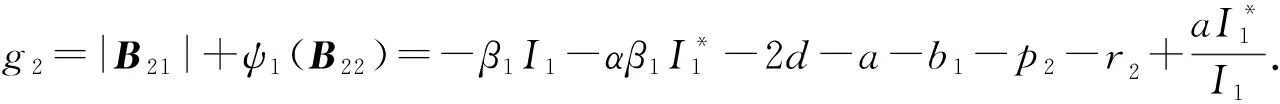
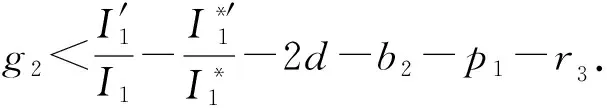
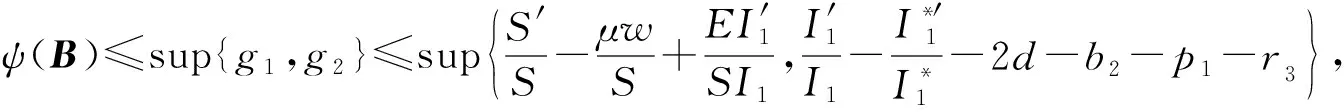
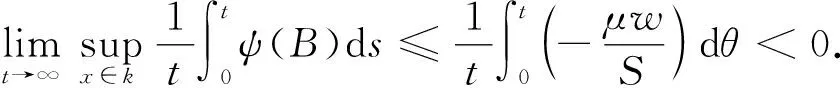
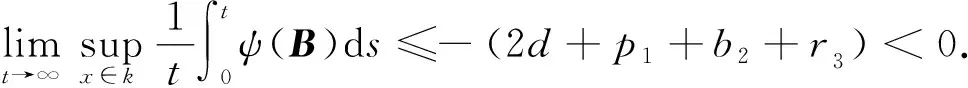
5 数值模拟
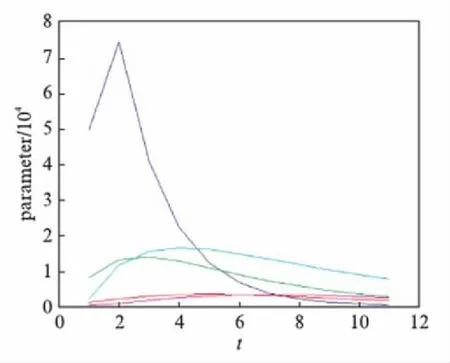
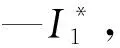
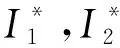
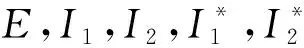
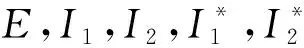
6 结 论