基于加权字典学习方法的低剂量CT图像重建
2018-06-13章程张健杜强李铭刘景鑫
章程,张健,杜强,李铭,刘景鑫
1.中国科学院苏州生物医学工程技术研究所,江苏 苏州 215163;2.长春市计量检定测试技术研究院,吉林 长春 130012;3.吉林大学中日联谊医院 放射线科,吉林 长春 130033
引言
由于计算机断层成像(Computed Tomography,CT)空间分辨率高、图像质量好,是一种广泛使用的医疗检查方法。然而,X射线的过度辐射会导致基因疾病和癌症[1]。降低辐射剂量主要通过降低X射线辐射强度或者减少采样率来实现,前者会造成重建图像噪声增加,信噪比降低,而后者是一个欠采样不完备投影数据重建问题。当利用以滤波反投影[2]算法为代表的解析重建算法进行重建时,由于采样率低于香浓奈奎斯特采样定理[3]的要求,重建图像中会有严重的混叠伪影,极大的影响了成像质量。
应对这种欠采样的重建问题,迭代重建算法有着极大的优势。2006年,由Candes等[4-5]提出的压缩感知(Compressed Sensing,CS)理论开拓了迭代算法的新方向[6]。该理论表明,信号可以在特定变换域被稀疏表示,从而可以突破采样定理的限制,用较低的采样频率观测和重构信号。以CS理论为基础,如今已出现了一些基于稀疏约束的欠采样重建算法。其中一类以全变分(Total Variation,TV)最小化为稀疏约束,具有代表性的算法有自适应最速下降—凸集投影(Adaptive Steep est Descent-Projection onto Convex Sets,ASD-POCS)算法[7]和梯度投影Barzilai-Borwein(Gradient Projection Barzilai-Borwein,GPBB)[8]算法。另一类算法的稀疏正则约束项由字典学习(Dictionary Learning,DL)方法生成,该方法是将待重建的CT图像分解为互相重叠的小图像块,这些图像块都可以用一个过完备字典(列数远大于行数的矩阵,每一列都叫做这个字典的原子)稀疏表示。2012年,Xu等[9]和Bai等[10]提出了基于字典学习方法的低剂量CT重建算法,得到了不错的重建结果。
然而,这些典型的稀疏重建算法在利用正则约束项抑制噪声的同时,在图像的低对比度信息区域也引入了相同的平滑效果。这种过平滑效应使图像的空间分辨率降低,细节信息丢失。为了保留更多的边缘细节信息,基于TV最小化的算法通过加入合理的自适应权重因子使算法能够自动分辨噪声和图像细节信息,从而抑制图像中低对比度信息区域的平滑效果,保留软组织边缘信息[11-12]。本文采用类似的优化策略,在字典学习算法模型中加入权重因子。通过对比Shepp-Logan投影数据和人体头部切片的重建实验结果,与未采用权重因子的算法相比,本文提出的加权字典学习算法重建质量更好,空间分辨率更高,噪声抑制效果更好。与联合代数重建(Simultaneous Algebraic Reconstruction Technique,SART)算法[13]和GPBB算法的结果对比也体现出了加权字典学习算法的优越性。
1 加权字典学习重建算法
1.1 字典学习重建模型
CT图像 的重建问题是一个典型的逆问题,投影数据采集过程可以表示为一个线性方程

其中 A={aij}∈RI×N2为系统矩阵;μ∈RN2×1为待求解的线性衰减系数分布,也就是待重建的CT图像,图像大小为N×N像素,重排得到一维向量μ;∈RI×1为测量的线积分投影数据。
在单色X射线源的假设下,CT投影测量值符合泊松分布规律:

其中b∈RI×1和 y∈RI×1分别为入射前和透射后的 X 射线强度;g=(g1,g2,K,gI)T∈RI×1为真实的线积分投影数据,其测量值为= ln(bi/(yi− γi));γi为读出噪声。
基于字典学习方法的重建问题可以表示为带有正则约束项的最优化问题:

其中ωi=(yi−γi)2/yi为统计迭代模型中的统计权重;是从N×N维图像中抽取N0×N0维小图像块的算子;图像块相互重叠,当抽取算子的滑动距离为1时,图像块的总数S=(N-N0+1)×(N-N0+1);为过完备字典被称为字典中的原子;as∈RK×1是图像块以字典D为基底的稀疏表示;λ与vs为正则化参数。最优化问题利用交替最小化方法求解,每一次迭代都分为两个连续的步骤——字典更新与图像更新。字典更新过程中,图像保持不变,目标函数简化为:

分别利用K-SVD(K Singular Value Decomposition)[14]算法和正交匹配追踪(Orhtogonal Matching Pursuit,OMP)[15]算法更新字典D和稀疏表示as,OMP算法设定稀疏度为一个定值,比如5~10,将式(4)的L0范数约束优化问题简化为OMP问题,此时求解不需要设定正则化参数vs的值。图像更新过程中,字典和稀疏表示不变,目标函数简化为:

利用可分离二次代理函数[16]方法,图像更新公式可以表示为:

1.2 权重因子
在字典学习重建模型中,式(3)中的正则约束项为:

上式中,对于不同的图像块,正则约束项的权重都相同,因此图像在迭代更新的过程中算法对不同区域的平滑效果相同,无法有效的在抑制噪声的同时保留图像细节信息。为了提高重建图像的质量和空间分辨率,本文提出根据图像块中所含边缘细节信息的多少选择适当的权重因子给予不同程度的平滑效果,图像块所含细节信息越多,权重因子越小。
由于图像块稀疏表示的求解通过OMP算法实现,且稀疏度为一个定值,因此图像块与其稀疏表示的残差可以间接反映细节信息的多少,残差越大,细节信息越多。本文选择上一次迭代结果的残差的反比例函数作为这一次迭代的权重因子,计算表达式为:

其中ε为保证算法稳定性的小量,Ct是所有图像块稀疏表示残差的平均值,是一个平衡参数,其作用是使当前计算出的权重因子不影响到目标函数中正则化参数λ的取值,加权字典学习重建模型的正则约束项变化为:

在每次迭代之前,权重因子根据上一次迭代结果自动更新,细节信息越多的图像块会倾向于得到一个越小的权重,使图像的低对比度信息得到更好的保留。由于权重因子的加入,图像更新过程的目标函数,即式(5)变化为:

图像更新公式(6)变化为:

1.3 最优化问题求解步骤
本文提出的算法以图像块残差作为权重因子的计算依据,称为加权字典学习(Weighted Dictionary Learning,WDL)算法。本文算法用有序子集凸优化[17](Ordered Subsets Convex,OSC)算法进行迭代加速,其具体求解步骤如下所示:① 步骤1:初始化,μ0为随机矩阵,D0为离散余弦变换矩阵,迭代次数t=0,权重因子=1;② 步骤2:用OSC算法迭代加速;③ 步骤3:用K-SVD算法更新字典得到Dt+1;④ 步骤4:用OMP算法更新稀疏表示得到;⑤ 步骤5:利用式(8)更新权重因子得到;⑥ 步骤6:利用式(11)更新图像,得到μt+1,迭代次数t=t+1;⑦ 步骤7:若满足迭代截止条件,停止迭代,返回重建结果,否则,返回步骤2。
迭代截止条件为:
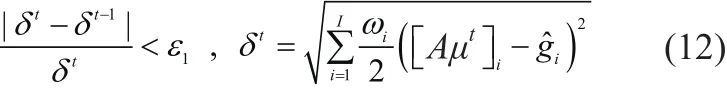
2 实验结果与分析
为了评估算法的性能,本文分别用Shepp-Logan标准体模和真实人体头部切片做数据仿真实验,投影几何为扇形束投影,投影角度均匀分布在360°范围内。对比算法为未加权重的字典学习算法,GPBB算法和SART算法。图像质量的客观评价标准为归一化平均绝对偏差(Normalized Mean Absolute Deviation,NMAD) 以 及 信 噪 比SNR:

可以看出,绝对偏差越小,信噪比越高,重建质量越好。正则化参数λ的选取利用文献[18]的自动选取模型。
在未加噪声的体模仿真实验中,Shepp-Logan标准体模的扫描和重建参数,见表1,重建结果,见图1;人体头部切片的扫描和重建参数与Shepp-Logan实验基本相同,不同之处是投影角度数变为180°,重建结果,见图2。

表1 Shepp-Logan体模扫描与重建参数

图1 Shepp-Logan标准体模仿真实验重建结果(无噪声)
通过对比发现,SART算法仅通过反投影差值平方最小化来重建图像,没有其他的先验知识和约束条件,因此重建结果最差,含有很多伪影。GPBB算法是一种TV最小化算法,能够出色的重建出图像的平滑区域,但从差值图像中可以看出在重建图像的边缘区域有过平滑效应,因此差值图像中有比较明显的边缘痕迹。未加权重的字典学习算法与GPBB算法相比,在重建上没有优势,平滑效果不如GPBB算法,在图像平滑区域有部分散粒噪声,但字典学习算法在图像边缘区域的过平滑效应也不如GPBB算法那么严重。本文提出的加权字典学习重建算法因为权重因子的引入,能够自动区分重建图像的平滑区域和边缘细节区域,从而给予不同程度的平滑效果,其与真实图像的差值图像,既没有明显的散粒噪声,也没有边缘痕迹,提高了重建图像的空间分辨率和成像质量。相比于未加权的字典学习算法,本文算法得到的结果的客观评价标准也有了很大的提高,其结果,见表2。

图2 真实人体头部切片仿真实验重建结果(无噪声)

表2 无噪声数据重建图像客观评价
两种字典学习方法在重建头部切片时的收敛速率,见图3。可以看到加权字典学习算法略微慢于未加权的算法,因为权重因子削弱了正则约束项对图像细节区域的平滑效果,使其收敛速度减慢。但与提高的成像质量相比,微小的收敛速度下降是可以接受的。

图3 头部切片重建NMAD随迭代次数下降曲线图
为了检验算法对噪声的鲁棒性,在人体头部切片的仿真实验中加入泊松噪声,设定入射前的X射线强度为120万光子数,透射物体后的探测光子数利用泊松分布模拟泊松噪声。重建结果,见图4。客观评价标准结果,见表3。结果与无噪声的方针实验结果相似,WDL算法结果的NMAD和SNR指标与GPBB算法接近。但是通过观察图中黄色边框内的放大区域,发现GPBB算法的过平滑效应导致图像中有比较明显的阶梯效应,其空间分辨率有所降低。从图4g可以发现,DL算法在有噪声的情况下对图像的高对比度边缘有过强的平滑效果。WDL算法虽然在一定程度上减弱了这种效果,但并没有完美的解决这个问题,这也是WDL算法结果的评价标准略差于GPBB算法的原因。

图4 真实人体头部切片仿真实验重建结果(有噪声)

表3 有噪声数据重建图像客观评价
3 结论
本文针对低剂量CT重建问题中,字典学习重建算法无法有效区分噪声和低对比度信息,重建图像容易丢失软组织边缘细节信息的问题,提出了一种通过权重因子保留细节信息,提高成像质量的加权字典学习算法。权重因子与图像块用字典稀疏表示的残差成反比,能够有效抑制迭代过程中对图像边缘的过平滑效应,同时保留了抑制噪声的能力,使抑制噪声和保留图像细节信息不再是相互制约的关系。仿真实验表明,提出的加权字典学习算法提升了字典学习算法的重建效果,其收敛速率相比未加权的算法仅有微小的下降。同时,与其他两种对比算法相比,本文提出的算法在提高图像空间分辨率上也有较大的优势。下一步研究需要探讨DL算法在有噪声的情形下对图像高对比度边缘的抑制效应并对其进行改进。
[1] De gonzález AB,Mahesh M,Kim K,et al.Projected cancer risks from computed tomographic scans performed in the United States in 2007[J].Arch Intern Med,2009,169(22):2071-2077.
[2] Liao HY,Sapiro G.Sparse representations for limited data tomography[A].IEEE International Symposium on Biomedical Imaging: From Nano To Ma cro, IEEE[C].2008:1375-1378.
[3] Jerri AJ.The Shannon sampling theorem—Its various extensions and applications: a tutorial review[J].P IEEE,1977,65(11):1565-1596.
[4] Candes EJ,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[M].New York:IEEE Press,2006.
[5] Ca ndes EJ,Tao T.Near-optimal signal recovery from random projections: universal encoding strategies?[J].IEE E T Inform Theory,2006,52(12):5406-5425.
[6] 焦鹏飞,李亮,赵骥.压缩感知在医学图像重建中的最新进展[J].CT理论与应用研究,2012,21(1):133-147.
[7] Sidky EY,Pan XC.Image reconstruction in circular conebeam computed tomography by c onstrained, total-variation minimization[J].Phys Med Biol,2008,53(17):4777-4807.
[8] Justin CP,Song B,Kim JS ,et al.Fast compressed sensing-based CBCT r econstruction using Barzilai-Borwein formulation for application to on-line IGRT[J].Med Phys,201 2,39(3):1207-1217.
[9] Xu Q,Yu H,Mou X,et al.Low-dose X-ray CT reconstruction via dictionary learning[J].IEEE T Med Imaging,2012,31(9):1682-1697.
[10] Bai T,Yan H,Shi F,et al.WE-G-18A-04: 3D dictionary learning based statistical iterative reconstruction for low-dose cone beam CT imaging[J].Med Phys,2014,41(6):527.
[11] Tian Z,Jia X,Yu an K,et al.Low-dose CT reconstr uction via edge-preserving total variation regularization[J].Phys Med Biol,2011,56(18) :5949-5967.
[12] Guo W,Yin W.EdgeCS: edge guided compressive sensing reconstruction[A].Visual Communications and Image Processing. International Society for Optics and Photonics[C].201 0:77440L-77440L-10.
[13] Andersen AH,Kak AC.Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algo rithm[J].Ultrasonic Imaging,1984,6(1):81-94.
[14] Aharon M,Elad M,Bruckstein A.rmK-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE T Signal Proces,2006,54(11):4311-4322.
[15] Tropp JA,Gil bert AC.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE T Inform Theory,2007,53(12):4655-4666.
[1 6] Elbakri IA,Fessler JA.Statistical image reconstruction for polyenergetic X-ray computed tomography[J].IEEE T Med Imaging,2002,21(2):89-99.
[17] Kamphuis C,Bee kman FJ.Accelerated iterative transmission C T reconstruction using an ordered subsets convex algorithm[J].IEEE T Med Imaging,1998,17(6):1101-1105 .
[18] Zhang C,Zhang T,Zheng J,et al.A Model of regularization parameter determination in low-dose X-Ray CT reconstruction based on dictionary learning[J].Comput Math Methods Med,2015:1-12.
