基于北斗GEO的电离层延迟修正方法比较与分析

薛凯敏,刘瑞华,王剑

(中国民航大学,电子信息与自动化学院,天津300300)

0 引 言

目前,全球导航定位技术迅速发展,我国的北斗卫星导航系统也已经按计划进入第三阶段的组网建设。为提高导航定位精度,需要减少或消除导航定位中的各类误差,导航信号传播路径中的电离层延迟是其中重要一项[1]。当前,各卫星导航系统和差分增强系统采用的电离层延迟修正方法有所不同,总体而言,应用较为广泛的有双频改正法、电离层模型法和格网改正法[2]。北斗卫星导航系统和全球定位系统(GPS)采用在长期观测数据基础上形成的经验模型Klobuchar模型来修正电离层延迟误差,从大尺度上保证了电离层预报的可靠性,在中纬度地区的改正效果一般在60%左右[3]。国内外众多学者在这方面进行了探讨与研究:霍星亮在其博士论文中提到基于长时间序列的电离层球谐函数系数与快速傅里叶变换法得到的广播电离层模型[4];章红平等提出的改进的Klobuchar模型,它是在原有8参数的基础上,顾及初始相位和夜间平场的14参数广播模型[3];李维鹏等利用松弛搜索方法来精化Klobuchar模型的参数[5];Schaer利用事后的欧洲定轨道中心(CODE)全球格网模型对Klobuchar模型参数进行优化,并给出预报的广播模型参数[6]。基于不同频率载波信号穿过电离层时产生的延迟量不同的原理,双频改正法利用双频伪距或载波相位观测量修正电离层误差,在全球范围内也得到广泛使用[7]。为对比两种方法在特定区域的修正效果,为天津地区提供有效的区域电离层误差修正方案,利用接收机采集到的卫星导航实测数据对两种方法进行分析计算,并以IGS发布的电离层格网数据为参考值对两种方法得到的结果对比分析。

1 北斗Klobuchar模型

将电离层假设为一层围绕地球的薄壳,其中心高度距离地球表面约为300～400 km.信号穿过电离层的传播路径随着卫星高度角E的变化而变化,高度角越小,信号传播路径越长,总电子数越多。通过给信号传播路径上的电离层延迟乘以一个倾斜因子可以求出观测点天顶方向的垂直电离层延迟[8]。

为计算简便,把电离层压缩为一个单层模型,称为中心电离层[9]。在北斗卫星导航系统中,中心电离层高度设置为375 km.如图1所示,K为导航信号从观测点P至卫星方向与中心电离层的交点,称为电离层穿刺点。

北斗导航电文中播发Klobuchar模型计算电离层延迟所用的8个参数[10],如表1所示。

表1 电离层延迟校正模型参数

则B1频点信号的电离层垂直延迟改正值可用公式(1)求得,单位为s:

(1)

式中:t为电离层穿刺点处的地方时(取值范围是0～86 400),单位为s,计算公式为

t=

(2)

式中:tE为用户测量时刻的北斗时,取周内秒计数部分;λM为穿刺点的地理经度,单位为弧度;A2为白天电离层延迟余弦曲线的幅度,用αn系数求得:

(3)

A4为余弦曲线的周期,单位为s,用βn系数求得:

(4)

式(3)、(4)中φM是电离层穿刺点的地理纬度,单位为弧度。与基于地磁坐标系的GPS Klobuchar模型不同,北斗Klobuchar模型采用地理坐标系,并限制周期A4在172 800 s内,且采用不同的地球半径(北斗地球半径值取6 378 km,GPS为6 371 km)、中心电离层高度(GPS中心电离层高度为350 km)[11]。但两者计算的电离层延迟均由广播参数、用户接收机经纬度、卫星高度角和地方时共同决定。

2 双频观测值求解电离层延迟

在仅考虑电离层延迟、对流层延迟及接收机钟差的条件下,北斗系统多频接收机测码伪距观测方程可以表示为[12]

P1=ρ+c(δtu-δt(s))+(Δρiono)1+Δρtrop,

P2=ρ+c(δtu-δt(s))+(Δρiono)2+Δρtrop,

(5)

式中:P1和P2分别为两个频率f1和f2测得的伪距观测值;ρ为卫星与接收机之间的真实几何距离; (Δρiono)1和(Δρiono)2分别为电离层引起的对应于频率f1和f2的群时延;c为真空光速; Δtu和(t(s))分别为卫星与接收机的钟差; Δρtrop为对流层延迟量。由式(5)可得到沿卫星信号传播路径上的电离层斜向电子总含量(TEC),即:

(6)

式中 :f1和f2分别为北斗B1和B2两个载波的频率。同理,利用载波相位观测量也可以得到电离层斜向TEC,即:

N1λ1-N2λ2),

(7)

式中:A=80.62 m3·s-2为电离层折射率;L1和L2分别为载波相位观测量;λ1和λ2分别为两个载波的波长;N1和N2分别为两个载波上的整周模糊度值。由伪距观测量得到的TEC是绝对测量值,而载波观测量得到的TEC是相对测量值,由于伪距测量噪声大于载波相位测量噪声,可以利用载波相位观测量平滑伪距观测量,从而获得传播路径上精度较高的TEC值。为此,通常采用引入平滑量Brs,从而得到高精度的斜向TEC值,即:

(8)

式中:M为一次卫星过顶的有效采样次数。则高精度的斜向TEC可以表示为

NTEC_s=NTEC_l+Brs.

(9)

由于卫星高度角不同,卫星信号到达某一测站时,其传播路径方向上的TEC值也不相同。天顶方向通过电离层的信号路径最短,因此,垂直方向上的总电子含量(VTEC)最少。通常所用电离层TEC参数实际上是垂直方向上的总电子含量,以TECu为单位(1TECu=1016电子数/m2)。在考虑硬件延迟的条件下,穿刺点处的VTEC可表示为

NVTEC=(NTEC_s-bs-br)·cosx,

(10)

式中:bs为卫星的硬件延迟;br为接收机的硬件延迟;x为卫星天顶角。然后采用卡尔曼滤波法计算卫星硬件延迟和接收机硬件延迟[13-14],从而得到穿刺点处的VTEC并利用式(11)将其转化为垂直电离层距离延迟,其中f为北斗卫星信号频率:

(11)

3 实测数据分析

为更好地对比Klobuchar模型与双频改正法的修正效果,以位于我国中低纬度地区的天津及其附近区域为例,利用NovAtel GPStation6接收机收集到的北斗GEO1号卫星实测数据进行计算,并以IGS发布的精度一般为2～8 TECu[15]的全球电离层格网数据作为参考值比较二者修正精度。

IGS以纬度间隔2.5°,经度间隔5°将全球划分为5 183个格网点,一天之内每2 h提供一幅全球电离层电子含量图,总计13幅图[16]。将IGS提供的格网数据进行双线性内插,即空间内插和时间内插,如图2及式(12)和式(13)所示,从而得到天津附近区域格网点数据,并将时间间隔从2 h缩短为60 s.

I(λ,φ)=I0,0×w0+I1,0×w1+I1,1×

w2+I0,1×w3

(12)

w0=(1-p)(1-q),

w1=p(1-q),

w2=pq,

w3=(1-p)q,

(13)

数据时间范围为2016年12月14日～20日,2017年2月14日～20日,2017年4月14日～20日,2017年6月14日～20日,共计28天。验证结果如图3～图6所示。图中电离层延迟值是指北斗B1频点信号的垂直电离层距离延迟,即时间延迟乘以电磁波传播速度。

日期Klobuchar模型/%双频解算值/% 2016年12月14日73.5482.62 2016年12月15日71.7581.20 2016年12月16日74.9182.34 2016年12月17日72.7183.69 2016年12月18日71.9082.58 2016年12月19日73.3381.53 2016年12月20日72.5981.59 2017年2月14日74.4782.82 2017年2月15日71.3182.25 2017年2月16日72.6281.62 2017年2月17日73.7483.40 2017年2月18日72.6581.51 2017年2月19日70.0382.17 2017年2月20日72.3583.34 2017年4月14日74.3182.67 2017年4月15日72.7083.27 2017年4月16日73.2981.93 2017年4月17日71.5380.26 2017年4月18日70.2579.94 2017年4月19日74.9584.53 2017年4月20日73.6782.58 2017年6月14日71.0480.46 2017年6月15日72.3582.51 2017年6月16日71.7980.65 2017年6月17日72.0881.51 2017年6月18日73.7483.40 2017年6月19日72.6581.51 2017年6月20日70.0382.17 平均值72.6382.11

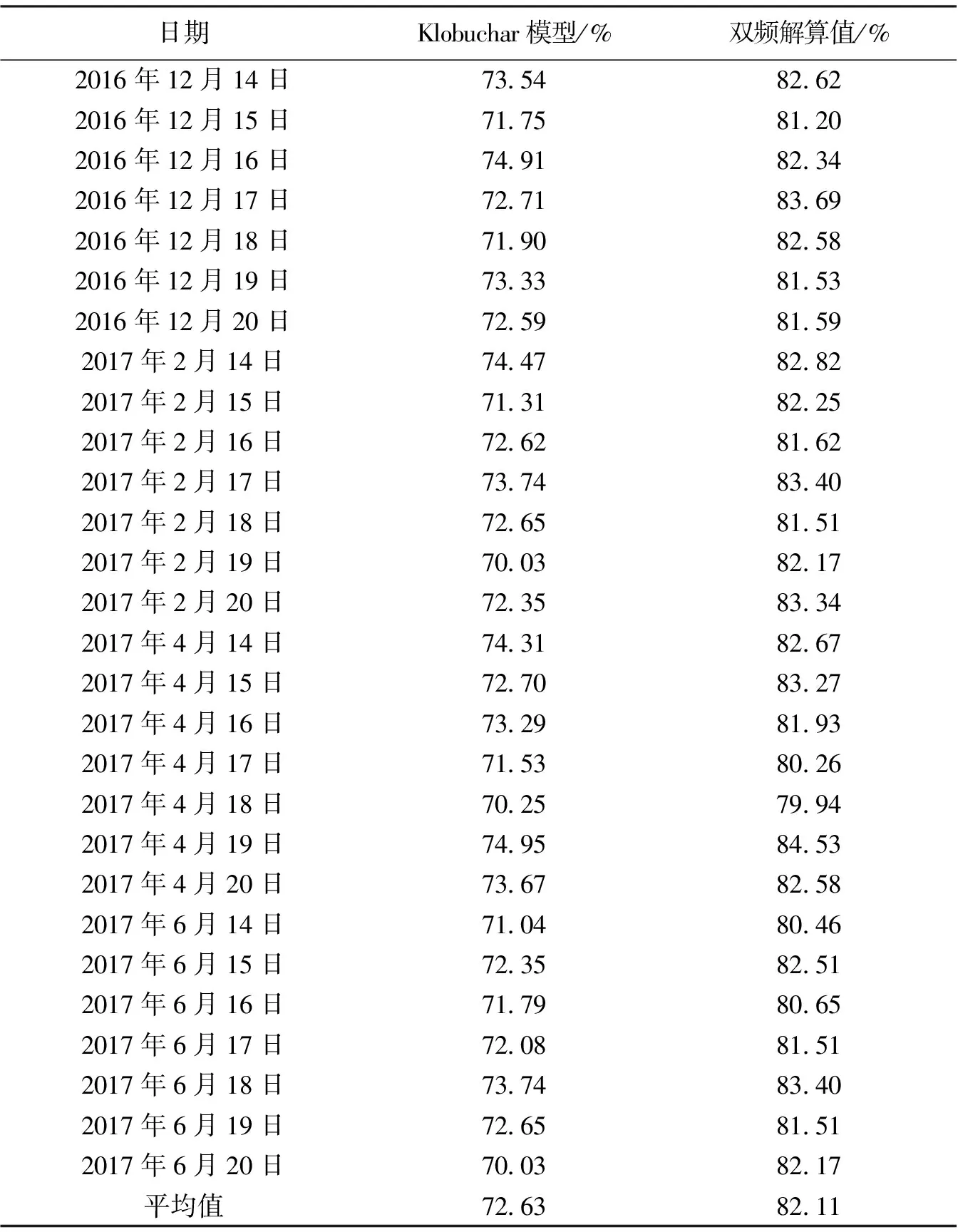
由计算结果可知,Klobuchar模型在白天修正效果较好,但在夜间修正效果明显下降。这是因为Klobuchar模型将电离层延迟的夜间平场设置为定值,受导航电文播发的8参数影响,实际测试情况下Klobuchar模型夜间的电离层延迟值每天有180 min左右为定值,时间较短,因此在上述图中并没有明显表现出该特征。而利用双频观测值解算电离层延迟有效的改善了这一状况,且白天的电离层修正效果也要优于Klobuchar模型。给出两种方法每天相对于IGS的平均修正精度统计结果,如表2所示。精度修正公式为

P=(1-|K-S|/S)×100%,

(14)

式中:K为Klobuchar原模型或双频解算的电离层时延值;S为IGS发布的电离层时间延迟值。

由统计结果可知,双频观测值计算结果每天的平均修正精度均高出Klobuchar模型10%左右,进一步验证了利用双频观测值解算电离层延迟在天津地区的可用性。

4 结束语

本文采用天津地区采集到的北斗实测数据对Klobuchar模型法、双频观测值解算法两种电离层延迟修正方法进行计算分析。结果显示,以IGS发布的全球电离层格网数据为参考值的情况下,双频观测值计算结果每天的平均修正精度均明显高于Klobuchar模型,平均高出9.48%,修正精度最高达到82.11%。研究表明,在天津及其附近区域采用双频观测值解算法修正电离层延迟效果更佳,从而为进一步提高区域北斗导航定位精度提供了重要参考。

[1] 许国昌.GPS理论、算法与应用[M].北京:清华大学出版社,2011.

[2] 刘基余,李征航,王跃虎,等.全球定位系统原理及其应用[M].北京：测绘出版社,1993,P137-140、144-151.

[3] 章红平.基于地基GPS的中国区域电离层监测与延迟改正研究[D].上海：中国科学院研究生院(上海天文台),2006.

[4] 霍星亮.基于GNSS的电离层形态监测与延迟模型研究[D].中国科学院测量与地球物理研究所, 2008.

[5] 李维鹏,李建文,戴伟.Klobuchar电离层延迟改正模型精化方法的研究[J].测绘科学,2009,34(5):49-51.

[6] SCHAER S. Mapping and predicting the earth's ionosphere using the global positioning system,[D]. Astronomical Institutes, University of Bern, Berne, Switzerland,1999.

[7] 吴雨航,陈秀万,吴才聪, 等. 电离层延迟修正方法评述[J].全球定位系统,2008,33(2):1-5.

[8] 王晓岚. GPS系统硬件延迟的估算方法研究[C].//第三届中国卫星导航学术年会电子文集——S08卫星导航模型与方法,2012.

[9] 白羽.电离层延迟模型区域优化技术研究[C].//第三届中国卫星导航学术年会电子文集——S05卫星导航增强与完好性监测,2012.

[10] BDS-SIS-ICD-2.0.北斗卫星导航系统空间信号接口控制文件(2.0版)[S].中国卫星导航系统管理办公室,2013.

[11] 李文文,李敏,胡志刚,等.两种电离层模型对卫星导航定位精度的影响分析[J].导航定位学报,2013,1(3):43-47.

[12] 王晓岚,马冠一.基于双频GPS观测的电离层TEC与硬件延迟反演方法[J].空间科学学报,2014,34(2):168-179.

[13] 高伟.赤道异常区电离层GPS-TEC与系统硬件偏差反演[D].中国科学院研究生院(空间科学与应用研究中心),2008.

[14] 李强,冯曼,张东和,等.基于单站GPS数据的GPS系统硬件延迟估算方法及结果比较[J].北京大学学报(自然科学版),2008(1):149-156.

[15] 徐李冰,蔡成林,陈光喜.一种新的北斗Klobuchar模型及其精度分析[J].大地测量与地球动力学,2015,35(5):788-792,796.

[16] 赵坤娟.区域电离层延迟误差改正方法研究[D].北京：中国科学院研究生院(国家授时中心),2014.