基于灰色关联TOPSIS法的舰船装备维修方案决策*

刘凌刚 ，耿俊豹 ，魏曙寰 ，徐孙庆

（1.海军工程大学舰船动力工程军队重点实验室，武汉 430033；2.海军工程大学动力工程学院，武汉 430033）

0 引言

舰船装备维修是一项复杂的系统工程，维修方案的差异将对舰船装备的可靠性和作战性能产生很大影响［1］。如何在兼顾各方面影响因素的基础上，通过一定的决策方法对现有的装备维修方案进行排序优选，是广大舰船装备管理人员非常关心的问题。

目前，关于舰船装备维修方案决策的研究已经有了较大发展。文献［2］根据装备的维修时间、维修费用等因素制定维修策略。文献［3］提出了只考虑经济性和装备可靠性影响因素的维修方案决策模型。文献［4］将装备维修决策定义为以装备可靠性、维修时间和维修费用为目标的决策问题。文献［5］通过可靠性理论对维修方案进行辅助决策，但考虑的评判因素过于简单。文献［6］利用层次分析法对方案评估决策。文献［7］考虑到方案信息的不确定性，将灰色决策用于维修方案决策中。但作为多属性决策问题的装备维修方案决策，在实际过程中往往受诸多因素的影响，存在决策信息不完整、不充分的灰色性情况，加上决策者的主观判断因素，使得装备维修方案决策更加困难，决策者需要进行全面分析［8-9］。而 TOPSIS法（理想解法）［10］是一种经典有效的多属性决策方法［11-12］，在项目评估和方案选优等方面已经得到了成功应用。

因此，根据舰船装备维修方案决策为多属性决策且方案信息具有灰色性的特点，本文提出一种基于灰色关联TOPSIS法的装备维修方案决策。该决策具有一定的全面性，选取维修间隔、维修费用、维修时间和维修风险4个量化指标，同时将灰色关联度和TOPSIS法相结合，通过对各维修方案相对贴近度排序优选得出最佳方案，使得决策过程和优选的舰船装备维修方案更合理可信。

1 相关理论和原理

舰船装备维修方案决策时，往往存在灰色性，通过灰色决策中的灰色关联度可以很好地挖掘方案信息的内在规律，解决该问题［13-15］。

1981年，Hwang和Yoon提出TOPSIS法，即通过逼近理想解进行排序解决多属性决策问题。其基本思路就是通过求解然后构造正理想方案和负理想方案，并利用量化指标求被决策方案与正理想方案和负理想方案的欧式几何距离，从而排序达到优选目的。

TOPSIS法具有方案信息使用较充分，丢失较少的优点。将TOPSIS法加入灰色关联度中形成灰色关联TOPSIS法，可以更好地体现方案数据曲线位置上的关系，可靠直观地描述指标值，集中反映方案决策信息的总体情况，为决策者进行综合评价分析提供参考。灰色关联TOPSIS法的原理就是通过确定维修方案量化指标后形成初始决策矩阵，在标准化处理后与权重集进行合成，变换成加权标准化矩阵从而得出正理想方案和负理想方案，最后计算出各方案到正理想方案和负理想方案的灰色关联度和欧式几何距离，最后合并得到各方案的相对贴近度，通过各方案的相对贴近度排序优选。

2 量化指标的确定

舰船装备时刻保持高的可靠性和优越的作战性能对于实现海洋强国的战略目标显得尤为重要，而舰船装备维修是其中的关键环节。舰船装备管理人员对维修方案的要求是用最低的成本和最少的时间使装备处于正常工作的状态，确保装备的可靠性和作战性能。因此，对舰船装备维修方案的要求可概括为：维修间隔长、维修费用少、维修时间短以及维修风险小。

2.1 维修间隔时间

装备维修之后的维修质量是维修方案决策的一个关键指标。在对装备进行维修或更换后，达到规定作战性能的程度称为维修质量。本文将维修间隔时间作为维修质量的量化指标。

2.2 维修费用

维修费用是装备维修方案决策中的重要指标，也是评价方案优劣不可或缺的。维修费用指的是保持装备正常工作而消耗的全部资源的货币形式，包括工时费用、备件费用、维修设施费用等。本文将装备维修的总费用作为维修费用的量化指标。

2.3 维修时间

时效性对于作战显得尤为重要，因此，对于装备维修方案来说，维修时间是必须考虑的因素。如果维修方案不考虑这一量化指标，很容易使装备不能按时投入使用，严重影响作战任务的完成。

2.4 维修风险

任何维修方案都会因为维修质量、维修费用、维修时间而面临失败的风险，所以在维修方案中也应该考虑方案可行性的大小，即维修风险。该指标可以通过“德尔菲法”来确定，利用专家打分从而统计出各方案的维修风险量化指标。

3 模型的建立

维修方案决策主要是根据现有的方案信息，利用一定的决策方法对方案进行排序然后优选。本文将灰色关联度和TOPSIS法相结合，形成灰色关联TOPSIS法。该方法的具体步骤如下。

3.1 将初始决策矩阵标准化

已知要决策的维修方案集和相对应的属性集分别为：，初始决策矩阵为：。其中cij为第i个方案ai在第j个属性bj下的属性值。

进行向量归一化：

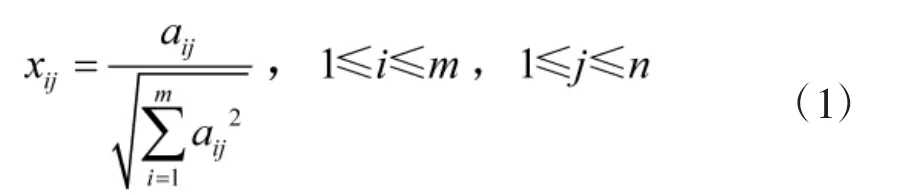
得标准化决策矩阵：。

3.2 确定属性权重集

确定决策方案属性权重集从而计算加权标准化矩阵。综合专家意见得到决策方案属性权重集为，通过广义合成算子将权重集W和标准化决策矩阵X进行Y=W·X变换，从而得到加权标准化决策矩阵，其中，。

3.3 确定正理想方案和负理想方案

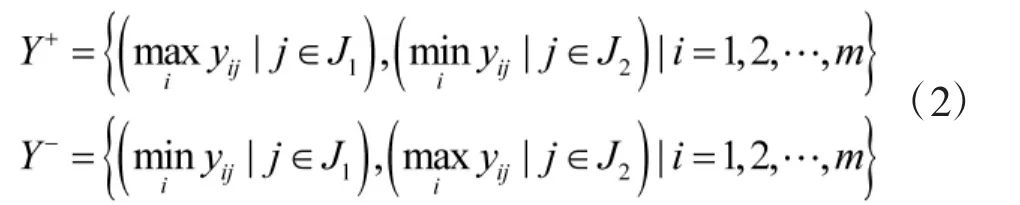
其中，J1为效益型指标，J2为成本型指标。

3.4 计算欧式几何距离

第i个方案到正理想方案的距离为：

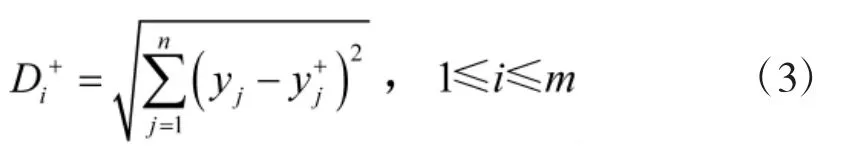
第i个方案到负理想方案的距离为：

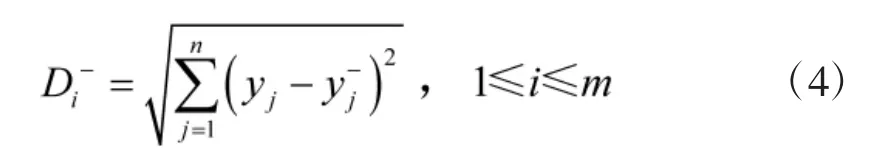
3.5 计算灰色关联度

第i个方案与正理想方案关于第j个指标的灰色关联系数为：

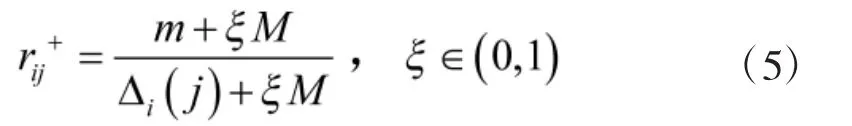
其中，，，为分辨系数，一般取为0.5。

则与正理想方案的灰色关联系数矩阵为：

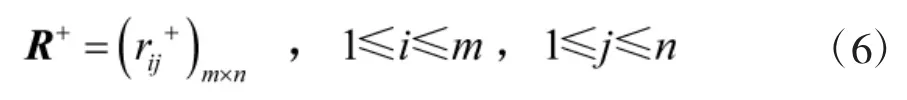
第i个方案与正理想方案的灰色关联度：

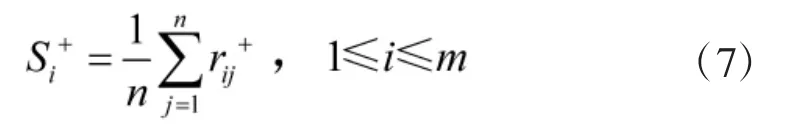
同理可得，与负理想方案的灰色关联系数矩阵为：

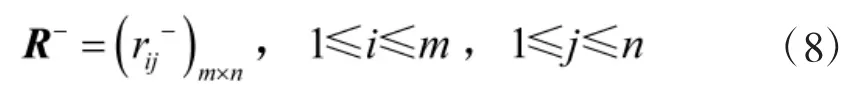
第i个方案与负理想方案的灰色关联度：

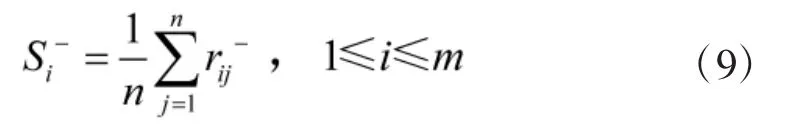
3.6 计算相对贴近度

对灰色关联度和欧式几何距离进行无量纲化处理，处理过程如式（10）所示。

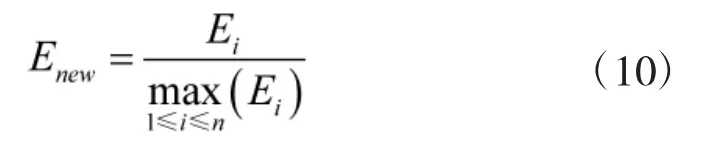
其中，Ei分别代表。

将无量纲化灰色关联度和欧式几何距离进行合并。合并公式为：

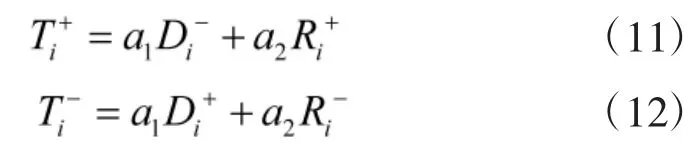
其中，a1、a2为方案决策者的偏好程度，并且满足a1+a2=1，方案决策者可以按自己的想法来确定它们的数值。

计算各方案的相对贴近度。

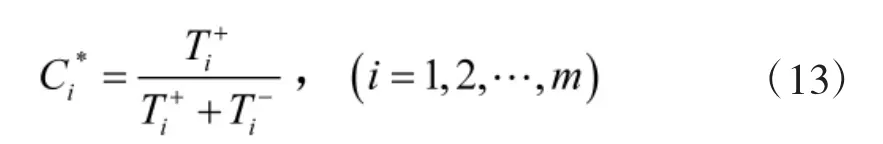
各方案的相对贴近度基于灰色关联度和欧式几何距离，意义明确，同时反映了各方案与正理想方案和负理想方案之间曲线的相似性差别和位置关系。通过计算相对贴近度的大小对各方案进行排序，相对贴近度越大则越好，反之则越差。

4 案例分析

某舰船装备的维修方案如表1所示。

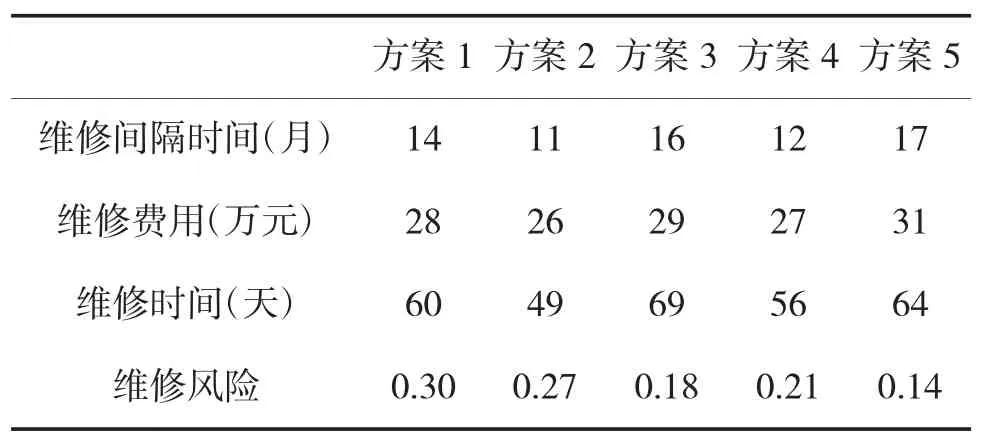
表1 某装备维修方案

4.1 基于灰色关联TOPSIS法的决策过程。

对表1构造的初始决策矩阵进行标准化处理，并综合专家意见得到方案各量化指标权重集，通过广义合成算子得到加权标准化矩阵。

量化指标权重集：加权标准化矩阵：

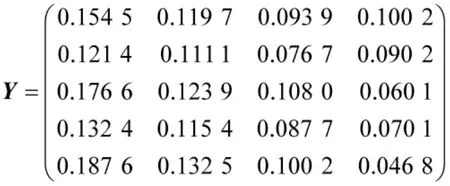
由于维修间隔时间为效益型指标；维修费用、维修时间和维修风险为成本型指标。则正理想方案和负理想方案分别为：

计算各方案到正理想方案和负理想方案之间的灰色关联度和欧式几何距离，并进行合并可得各方案的相对贴近度，如下页表2所示。

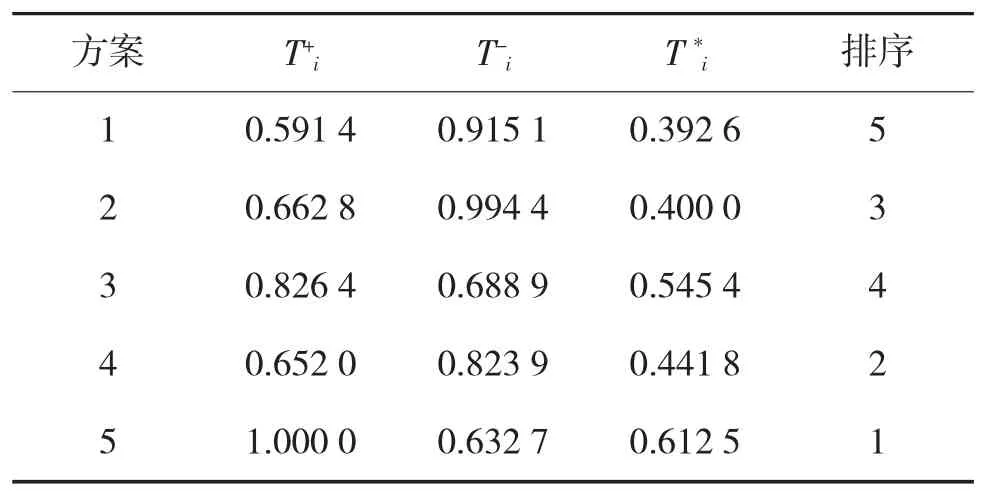
表2 各方案的相对贴近度和排序

由表2可知，最终的舰船装备维修方案排序为方案5、方案3、方案4、方案2、方案1。

4.2 灰色关联度法和灰色关联TOPSIS法对比。

通过灰色关联度法求得各维修方案相对贴近度分别为：0.4452、0.4887、0.5057、0.5040、0.5578。说明灰色关联TOPSIS法的排序结果和灰色关联度法的排序结果相一致，均为方案5、方案3、方案4、方案2、方案1。灰色关联TOPSIS法在舰船装备维修方案决策中有效可行。

将上述两种方法计算出的各维修方案的相对贴近度进行归一化处理，即各个维修方案的相对贴近度与所有维修方案相对贴近度之和的比值。归一化的相对贴近度如表3所示。

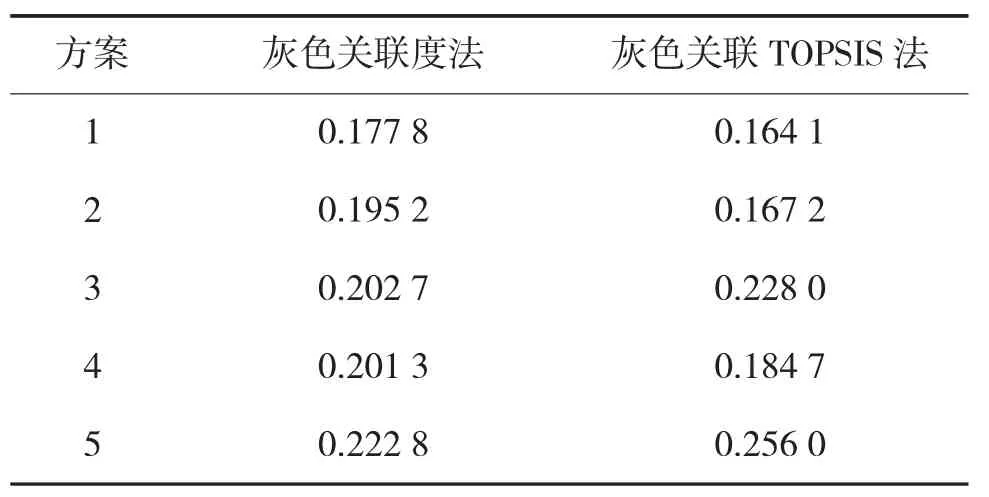
表3 归一化的相对贴近度

绘制散点图如图1所示。

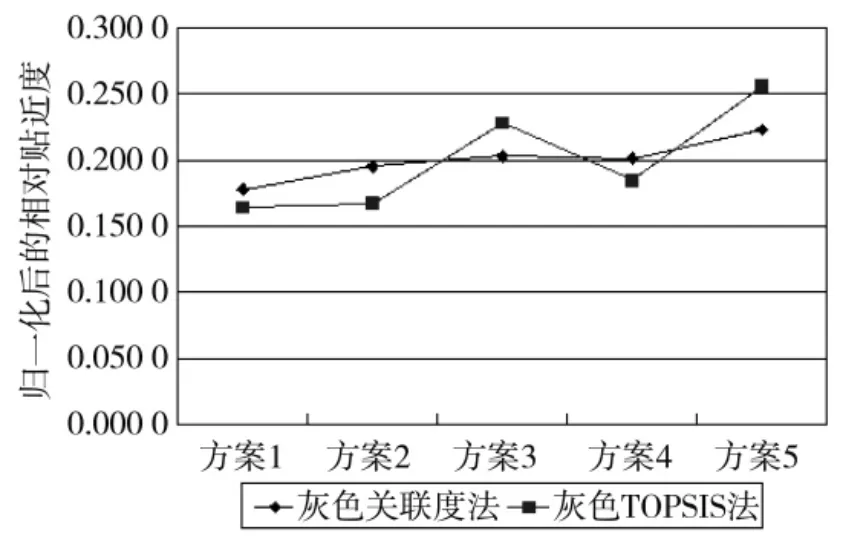
图1 归一化的相对贴近度散点图

求得维修方案排序后，计算两种方法中相邻两个维修方案的区分度，区分度的值越大，说明该方法在对维修方案的区分中更强，更容易选出好的方案。区分度为优劣排序相近的两方案贴近度差的绝对值与所有方案贴近度平均值之比。两个方法的区分度如表4所示。

根据图1和表4可知，在各舰船装备维修方案排序相同的情况下，灰色关联TOPSIS法比灰色关联度法有更强的区别能力，更能区分排序相邻的两个维修方案的优劣，具有更高的精度。因此，灰色关联TOPSIS法计算的舰船装备维修方案排序结果更具说服力。

表4 区分度比较值

5 结论

舰船装备维修方案决策是一个多属性决策问题，本文把维修间隔时间、维修费用、维修时间和维修风险作为维修方案决策的4个量化指标，将TOPSIS法加入灰色关联度中形成灰色关联TOPSIS法，同时考虑各维修方案到正理想方案和负理想方案的灰色关联度和欧式几何距离，通过计算舰船装备维修方案的各相对贴近度排序优选。某舰船装备维修方案的应用案例说明，该方法有效可行，且比灰色关联度法具有更高的区分度。

［1］訾书宇，魏汝祥，王丹.基于多属性群决策的舰船维修方案组合评估方法 ［J］. 舰船科学技术，2011，33（3）：127-130，134.

［2］全文彬，彭鹏菲，黄傲林，等.复杂舰载装备系统维修决策分析［J］.舰船电子工程，2013，33（2）：109-112.

［3］张勇，李汉升，孙文彬，等.基于经济性-可靠度的雷达装备维修决策模型研究［J］. 装备学院学报，2013，24（4）：114-118.

［4］赵金超，颜静波，陈雅.舰船装备多态系统维修决策的帕累托最优模型 ［J］. 火力与指挥控制，2014，39（6）：131-134.

［5］贾希胜.以可靠性为中心的维修决策模型［M］.北京：国防工业出版社，2007：1-5.

［6］杨波，陈雅，刘佳.基于目标规划的舰船装备海上维修决策模型［J］.海军工程大学学报，2013，25（3）：91-96.

［7］王有元，徐海霞，陈伟根，等.电力变压器状态维修策略的灰局势决策方法 ［J］. 重庆大学学报，2009，32（12）：1419-1424.

［8］徐玖平，吴巍.多属性决策的理论与方法［M］.北京：清华大学出版社，2006.

［9］蔡志强，孙树栋，司书宾，等.不确定环境下多阶段多目标决策模型 ［J］. 系统工程理论与实践，2010，30（9）：1622-1629.

［10］CHEN C T.Extensions of the TOPSIS for group decision making under environment［J］.Fuzzy Sets and Systems，2000，114：1-9.

［11］LEE A H I，CHEN H H，KANG H Y.Multi-criteria decision making on strategic selection of wind farms［J］.Renewable Energy，2009，34：120-126.

［12］YE Y X，MI Z C，WANG H Y，et al.A bayesian networks based method for multiple attributes decision making under uncertainty ［J］.Systems Engineering-Theory&Practice，2007，27（4）：107-113.

［13］傅健，王明为，阮旻智.舰船装备舰员级维修精细化管理研究［J］.兵器装备工程学报，2017，38（8）:76-80.

［14］LIU S F.On measure of grey information［J］.The Journal of Grey System，1995，2：97-101.

［15］冯建湘，唐嵘，高利.灰色推理技术及其智能应用研究［J］.计算机工程与科学，2006，28（3）：131-133.

［16］翟楠楠，刘晓东，吴诗辉，等.基于CCA/DEA的装备维修保障绩效评价 ［J］. 火力与指挥控制，2016，41（12）：44-49.