海上机动目标均匀概略航向下的散布规律研究*

侯学隆，姜青山

（海军航空大学岸防兵学院，山东 烟台 264001）

0 引言

现代反舰作战，为了充分发挥各型作战平台装备的中远程反舰导弹的射程优势，遂行远距、精确与隐蔽攻击水面目标任务，基于远程目标指示信息的超视距导弹攻击已成为基本作战样式［1］。在反舰导弹超视距攻击目标捕选决策中，基于稳妥的战术原则考虑，通常假设目标航向分布在2π范围内来估计最大散布范围［2-3］，将射击瞄准点定格在目标指示点，并以导弹开机覆盖目标最大散布圆来计算末制导雷达最小搜索扇面角［4-5］。

水面舰艇海上航行通常以遂行作战任务为牵引，机动航向带有鲜明的指向性，在大多数情况下可以视作近匀速直线运动，突然倒车逆向机动的可能性非常小［6］。如果指挥决策人员根据战场态势和目标机动的大趋势，判断出目标的概略航向，接下来考虑几个问题：1）概略航向下反舰导弹的射击瞄准点是不是还选择在目标指示点，如果不是，该如何确定。2）末制导雷达应搜索覆盖的重点区域如何确定。

解决以上两个问题的关键在于确定目标的位置散布规律。通过位置散布规律可以确定目标高概率密度区域，为射击瞄准点及末制导雷达角度搜索范围、距离搜索范围的使用优化提供依据。为此，本文重点研究海上机动目标概略航向下的位置散布概率密度及其性质，通过散布规律的仿真分析回答上述两个问题。

1 海上机动目标均匀概略航向下的位置散布概率密度

1.1 基本假设

为方便模型建立，作如下假设：

1）侦察预警兵力对海上机动目标定位的均方差为σmz.（σmz.＞0）、系统误差为零，即目标初始位置散布服从二维正态圆分布。

2）指挥员给出的概略航向信息包括两个：一是目标航向角分布范围ΔC，ΔC∈（0，π）；二是主航向角Cc，为航向分布范围的角平分线与正北之间的夹角，Cc∈［0，2π］。定义目标运动矢量与正北之间的夹角为目标航向角，记为c，c位于“|c-Cc|≤ΔC/2”所定义的区间。显然，c为随机变量，假设c服从均匀分布。与正态分布相比，假设航向角服从均匀分布属于保守型决策。

3）目标机动时间t以远程目标指示系统获取目标定位信息时刻为零点计算。在反舰导弹对海上机动目标射击时，该时间主要与反舰导弹的自控飞行时间有关。

4）目标在机动时间t内作匀速直线运动，运动速度为v，v为确定性变量。

在上述假设条件下，海上机动目标概略航向下位置散布的基本含义是：在初始位置散布服从系统误差为零的正态圆分布（Circular Normal Distribution，CND）下，目标以确定速度（Certain Speed，CS）和均匀概略航向（Approximate Course under Uniform Distribution，ACUD）机动一段时间后引起的位置散布。该散布在本文中统称为“CND-CSACUD散布”。

在CND-CS-ACUD散布中，目标将以初始位置散布点为基准，在［-ΔC/2，ΔC/2］内任意方向机动，如图1（a）所示。这与目标背离初始散布中心作径向机动是有区别的，如图1（b）所示。以目标背离初始散布中心作径向机动为假设条件［7-8］来建立CND-CS-ACUD散布模型将存在一定误差。

图1CND-CS-ACUD散布概念图

1.2 目标初始位置及航向散布概率密度

根据CND-CS-ACUD散布的基本内涵，侦察预警兵力对海上目标定位服从正态圆分布，定位系统误差为零。以目标定位点为原点建立OXY直角坐标系，其中OX轴与航向分布范围的角平分线平行且同向（即指向Cc方向），OY轴符合右手定则，如图1所示。则目标初始位置 M（xmb0，ymb0）的概率密度为［9］：

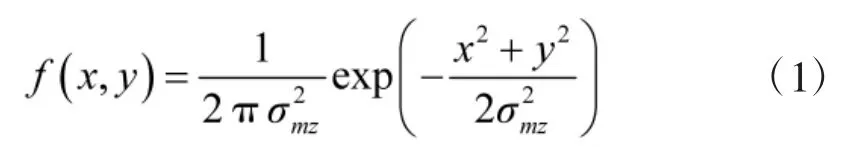
目标航向角c服从均匀分布，其在ΔC范围内任何一个方向的概率密度是均等的，概率密度fc（c）如下式所示：

上式中的概率密度均位于“|c-Cc|≤ΔC/2”所定义的区间，当c取其他值时概率密度为零。

定义目标航向偏离主航向的角度为航向差角，记为α，顺时针为正，逆时针为负，α∈［-ΔC/2，ΔC/2］。则：

由于航向角c服从均匀分布，根据上式，航向差角也服从均匀分布，其概率密度fα（α）为：

式中，α∈［-ΔC/2，ΔC/2］。

当ΔC为2π时，上式变成了未知航向下的散布概率密度。

1.3 目标机动后的CND-CS-ACUD散布概率密度

CND-CS-ACUD散布中，目标将以任意一个初始位置散布点为基准，在［-ΔC/2，ΔC/2］内任意方向机动，如图1所示。设目标从初始散布位置M（xmb0，ymb0） 开始机动，t时间后到达位置 P（xmb，ymb），则：

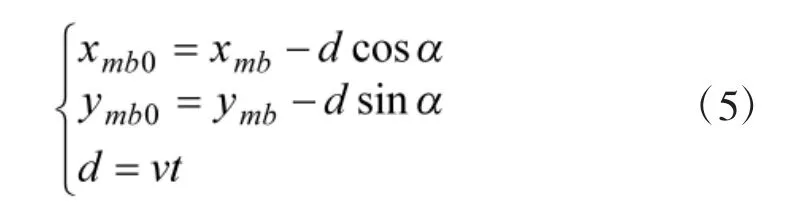
式中，α∈［-ΔC/2，ΔC/2］；d 为目标机动距离。

由上式可知，P（xmb，ymb）为二维随机变量。结合式（5）和式（1），在目标航向差角α与初始散布位置独立时，则在给定 α 的条件下，位置点 P（xmb，ymb）的条件概率密度［10］k（x，y|α）为：

由条件概率密度及随机变量α的概率密度，可得随机变量（xmb，ymb，α） 的联合概率密度 k（x，y，α）为：

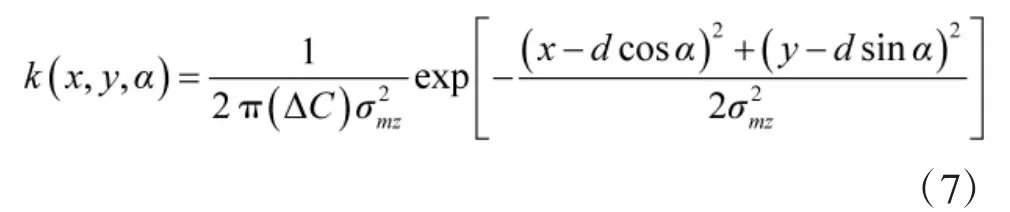
对 k（x，y，α）在 α 维度积分可得 P（xmb，ymb）的边缘概率密度 g（x，y）为：

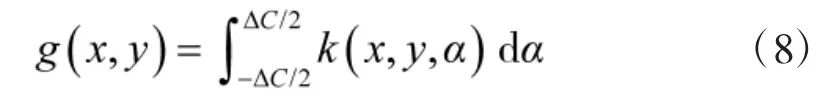
式中：x∈（-∞，+∞），y∈（-∞，+∞）。上式即为海上机动目标均匀概略航向下的位置散布概率密度表达式，仅与σmz、ΔC、d 3个参数有关，给定任意x、y时，可求出概率密度的数值解。

假设散布圆圆心为（xk，yk），半径为 R，则目标落入该圆的概率为：

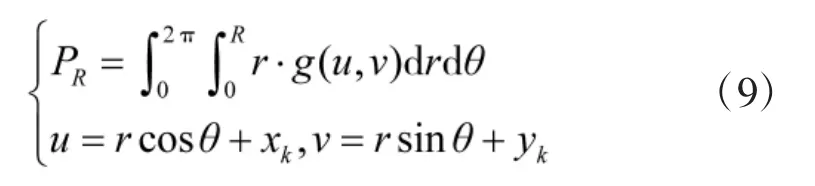
2 CND-CS-ACUD散布概率密度的性质

性质：对于任意的 x、y∈（-∞，+∞），有：g（x，y）=g（x，-y）。

证明：令f（α）=k（x，y，α），将x=rcosθ、y=rsinθ代入 k（x，y，α），可得：

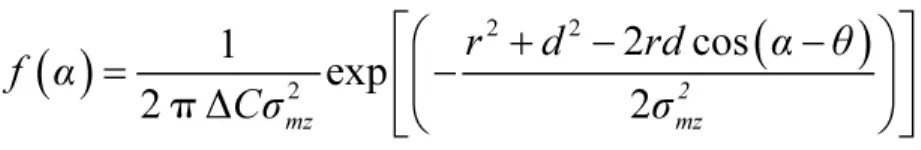
显然，f（α）可积。

企业重组业务不同于企业常规的经营性业务，需要企业全体人员做好充分的准备迎接企业重组带来的困难和风险。税务工作贯穿企业重组的全过程，实现税务风险合理控制、进行纳税筹划、加强税收管理具有一定的必要性。企业应该在整体战略目标的指引下，设计科学合理的税收筹划方案，降低企业重组业务的税务风险，减少税收负担，推动企业重组业务顺利进行，创造企业效益和社会效益的双赢。

在图1所示的OXY坐标系下，设A、B两点关于 ox轴对称，A 点的坐标为（xa，ya），B 的坐标为（xb，yb）。令 xa=rcosθ、ya=rsinθ，则 B 点的坐标为 xb=rcos（-θ），yb=rsin（-θ）。将 A、B 两点的坐标分别代入f（α）中，可得：

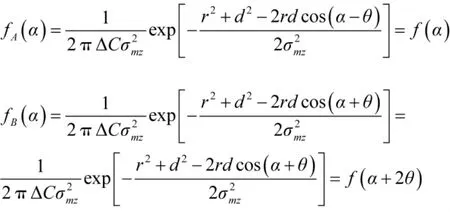
A点的概率密度为：

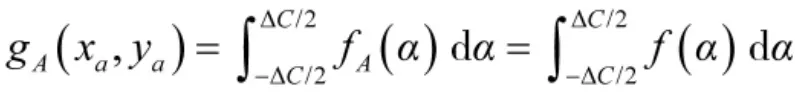
令 α=t+θ，可得：

B点的概率密度为：

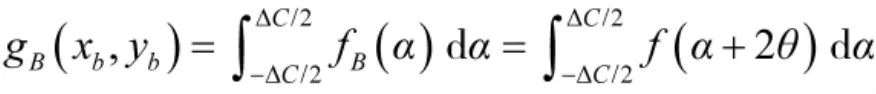
令 α=t-θ，可得：

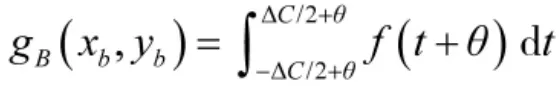
令k（t）=f（t+θ），可得：

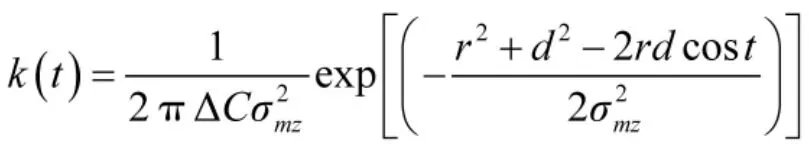
由于 k（t）=k（-t），可知 k（t）是偶函数。

考虑到k（t）是偶函数，上式的第1项、第2项可变为：

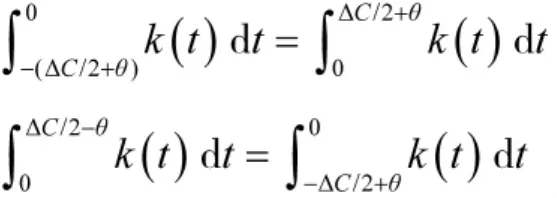
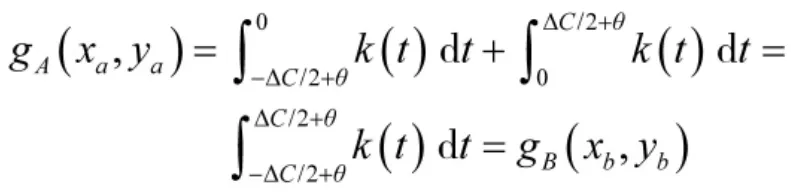
由于 A、B 关于 ox轴对称，因此，有：g（x，y）=g（x，-y）。即 CND-CS-ACUD 散布在直角坐标系下的概率密度关于航向分布范围的角平分线对称。

证毕。

3 仿真计算分析

计算条件：（a）侦察预警兵力对目标定位均方差σmz=4 km；（b）目标航向分布范围ΔC分别为π/2、π/4、π/8、π/16，主航向角 Cc均为零；（c）目标机动距离d=20 km。计算结果如图2所示。

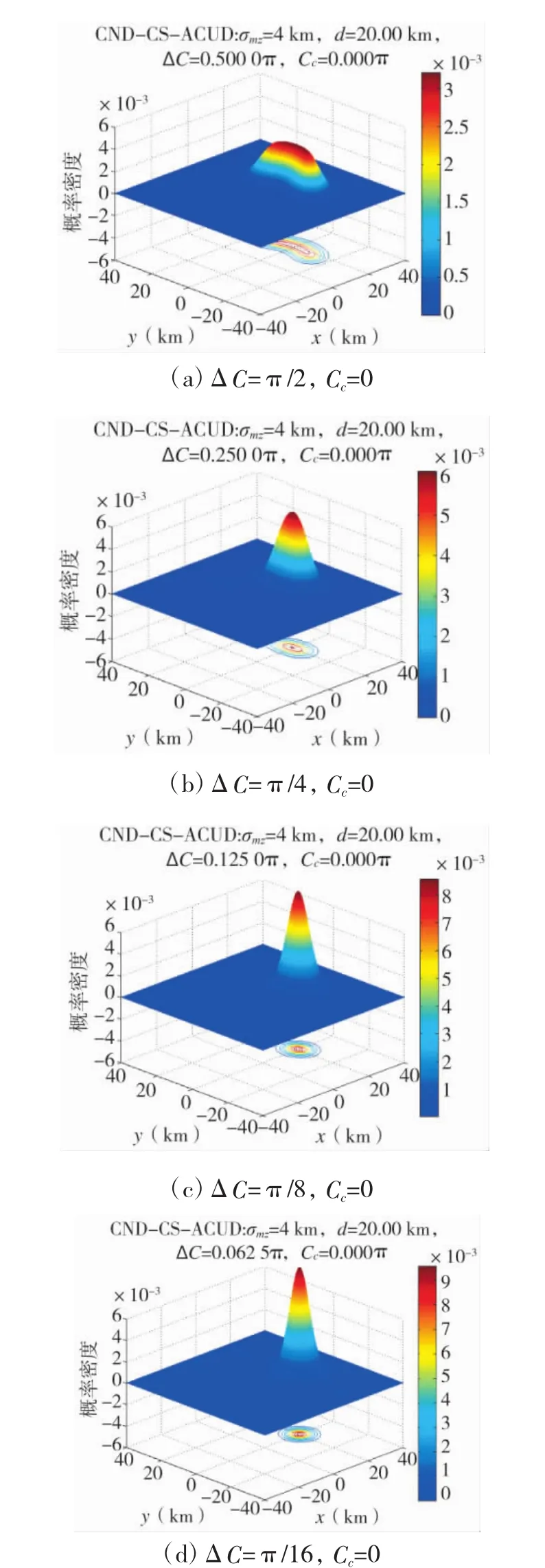
图2 CND-CS-ACUD散布概率密度

对数据及图形特征进行分析，有：

1）在直角坐标系下，CND-CS-ACUD散布的概率密度均关于过航向分布范围角平分线的垂面对称，这从侧面验证了前文所述性质的正确性。

2）航向分布范围ΔC对散布区域具有显著的影响，ΔC越小，高概率密度区域越集中，目标散布区域越小。如果能利用各种可能的先验知识及战场态势尽量缩小目标航向分布范围，可以大幅减小目标散布区域。

3）CND-CS-ACUD散布的概率密度最大值可能有多个，但必有一个位于航向分布范围角平分线（dud，0）处。dud的计算结果如表1所示。

表1 最大概率密度取值点计算结果（单位：km）

由表1可知，当ΔC越小，dud越趋近于d，但始终小于 d。利用此结论，将坐标由（d，0）向（0，0）方向滑动，可通过程序快速求取最大概率密度的取值点。该取值点周边区域目标出现的可能性最大，因此，该点可作为反舰导弹的射击瞄准点。

4）散布区域可用圆形（当ΔC较小时）或概率密度等值线外接矩形（当ΔC较大时）来表征。为方便求解圆形或矩形散布区域，可将最大概率密度取值点作为圆心或矩形中心点，逐步向周边扩散，累加区域概率，直到概率达到给定要求时，停止计算，此时便可计算出给定概率下的散布区域。该区域就是目标高概率出现区域，反舰导弹的末制导雷达搜索区应重点覆盖此区域。

以目标落入散布圆概率99.00%作为依据，对CND-CS-ACUD散布在不同航向分布范围下的散布圆半径Rg计算结果如表2所示。显然，该散布区域小于现在点射击时以目标指示点为圆心的散布圆Rq（目标落入概率为99.00%时，将ΔC=2π代入式（9）解算得29.64 km），可大大减小末制导雷达的角度与距离搜索范围，对隐蔽搜索、多目标选择极为有利。

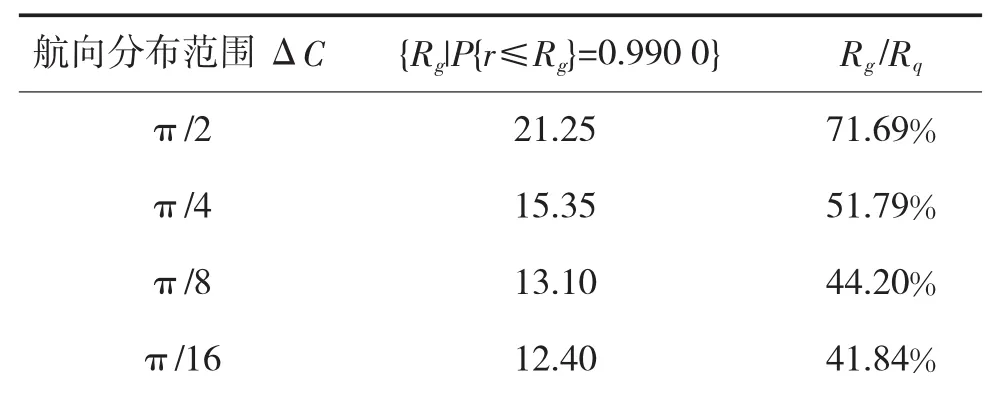
表2 以（dud，0）为原点的散布圆半径（单位：km）

4 结论

推导了初始位置服从正态圆分布、以确定速度和均匀概略航向机动下的CND-CS-ACUD散布概率密度模型，研究该散布的性质特征，得出以下结论：1）在直角坐标系下，CND-CS-ACUD散布的概率密度关于过航向分布范围角平分线的垂面对称。利用此结论，可以将目标落入对称散布区域概率的积分计算量减少一半。2）CND-CS-ACUD散布的最大概率密度取值点必有一个位于航向分布范围的角平分线上。取值点与原点的距离接近d，但始终小于d。在σmz、d相同的情况下，ΔC越小，取值点与原点的距离越逼近d。以d作为起始点，可通过程序快速求取该取值点。3）最大概率密度取值点可作为反舰导弹的射击瞄准点，以该取值点为中心的目标高概率散布区域可作为反舰导弹末制导雷达角度、距离搜索范围计算的依据。4）对CND-CS-ACUD散布概率密度进行积分，可获取目标落入给定区域概率。如果给定区域为反舰导弹的搜捕区域，则计算出来的是反舰导弹的搜捕概率。由此可见，该散布模型在反舰导弹搜捕概率解析计算方面具有重要应用价值。5）利用随机变量的互不相关性，基于条件概率密度方法可以建立不同初始位置散布、航向散布、速度散布组合情况下的复杂散布概率密度模型。该方法在构建多维随机变量概率密度模型方面十分有效。

CND-CS-ACUD散布模型不仅可用于反舰导弹目标搜捕决策方面，也可推广到航空搜潜、侦察卫星引导无人机对海搜索区域规划等领域，具有较为广泛的应用前景。下一步将基于CND-CS-ACUD散布规律研究目标航速变化情况下的稳妥散布区计算方法。

［1］侯学隆，姜青山.多种因素影响下的反舰导弹搜捕能力建模分析［J］.海军大连舰艇学院学报，2017，41（1）：23-27.

［2］景永春，谢春思，熊正详，等.基于目标散布的反舰导弹捕捉概率研究［J］.战术导弹技术，2016，37（4）：188-193.

［3］曾家有，宋友凯，严建钢.基于目标位置误差圆分布的舰舰导弹捕捉概率计算模型［J］.战术导弹技术，2010，17（2）：55-58.

［4］高青伟，曾家有，吴芳，等.惯性导航系统动基座对准对舰舰导弹捕捉概率的影响［J］.兵工学报，2016，37（1）：91-94.

［5］曾家有.各种因素对现在点射击方式反舰导弹捕捉概率的影响分析［J］.兵工学报，2011，32（6）：719-724.

［6］徐一帆，谭跃进，贺仁杰，等.天基海洋目标监视的系统分析及相关研究综述［J］.宇航学报，2010，31（3）：628-637.

［7］胡啸，林剑峰，刘林立.卫星侦察舰船目标分布预测及效能分析［J］.计算机测量与控制，2012，20（6）：1580-1584.

［8］刘维国，王警警.飞行器对目标区域搜索模型研究［J］.舰船电子对抗，2012，35（5）：28-31.

［9］马拴柱，刘飞.地空导弹射击学［M］.西安：西北工业大学出版社，2012：140.

［10］盛骤，谢千式，潘承毅.概率论与数量统计［M］.北京：高等教育出版社，2005：83-90.