航空产品外场使用可靠性评估方法*
2018-06-13蔡忠义陈云翔项华春
蔡忠义 ,张 强 ,2,陈云翔 ,项华春
(1.空军工程大学装备管理与安全工程学院,西安 710051;2.中国航天科技集团防御技术研究院,北京 100854)
0 引言
航空产品是指构成航空装备所涉及的一系列成品和维修设备的统称[1]。按照产品层级不同,可分为系统级、设备级、功能模块级、器件级。由于设备级航空产品(机载设备)在飞机上具有独立功能、便于外场拆卸更换,也称外场可更换单元(Line Replace Unit,LRU)[2]。通过收集机载设备在部队外场的使用与故障数据,开展外场使用可靠性评估,对于摸清产品真实可靠性水平和开展后续产品质量提升与可靠性改进决策具有重要意义。
当前对于机载设备外场使用可靠性评估研究需考虑以下问题:
一是外场数据存在部分缺失的情况。航空产品外场数据一般具有样本量大、含随机截尾、部分故障信息缺失等特征。王星博等提出了基于自助抽样仿真的外场故障时间缺失样本数据处理方法,结合外场收集到的某航空发动机故障样本数据,验证了所提方法的正确性[3]。张显余等针对航空兵部队外场故障信息流失情况,提出了故障信息流失补偿方法,采用残存比率法来计算随机截尾数据的经验分布函数[4]。
二是区分完全修复与基本修复的产品修复特点。设备级产品按照故障后是否可修复,分为可修复产品和不可修复产品。按照修复后技术状态,将可修复产品分为完全修复产品和基本修复产品。
对于完全修复件的可靠性评估,可采用经典概率分布模型来建模,其中具有随机截尾特征的产品经验分布函数计算,一般可采用残存比率法、平均秩次法和寿命表法等[5]。巨向斌等结合自身工作经验,详细论述了寿命服从指数分布的电子系统和设备的MTBF估计模型,分析了外场可靠性数据处理方式,给出了开展外场可靠性评估工作建议[6-7]。对于基本修复件的可靠性评估研究,崔毅勇等建立了基于非齐次泊松过程的基本修复产品可靠性评估模型,用故障强度来描述修复后产品故障规律[8]。沈峥嵘等结合某型弹药的存储数据,给出了其平均储存寿命和可靠度的估计值[9]。
基于上述研究,本文首先研究了一种随机数值模拟的信息缺失处理方法,然后建立了考虑多因素影响程度的设备运行比确定模型,最后区分产品修复状态,分别提出了外场可靠性评估方法并加以实例分析。
1 外场故障信息缺失处理方法
针对外场部分故障信息流失的情况,处理方法是采用随机数值模拟的方法,产生含故障发生日期的伪随机故障样本。
假设任务或统计期间内有r个故障数据,其中有u个故障发生时间缺失的故障样本,r-u个完整故障样本按照故障发生时间的先后进行排序为,采用蒙特卡罗数值仿真的方法,采用u个含故障发生日期的伪随机故障样本。具体步骤如下:
1)在横轴为时间、纵轴为分布概率密度的坐标系中绘制完整故障样本的经验分布直方图;
2)在直方图区域中按照平均分布随机产生u个数据点;
3)取u个数据点的横坐标构成了u个含故障发生日期的伪随机故障样本;
4)重复上述步骤至仿真次数达到N,结束仿真。
上述随机生成的N组伪随机故障样本,分别参与可靠性评估,都可得到一组参数估计值,最后取均值,即可得到参数的估计均值。
2 考虑多因素影响程度的运行比确定模型
航空兵部队对于每架飞机的逐架日飞行时间有着严格和规范的记录,但对于机载设备的工作时间是没有记录或难以记录,近似做法是认为机载设备的工作时间与载机(该设备所安装的飞机)飞行时间之间存在一定的比值关系,称为运行比,计算公式表示为:

式中,l0表示某机载设备的运行比;Tw为设备的工作时间;Tf为期间载机的飞行时间。
目前,对于设备运行比一般采用经验法或统计法来确定。经验做法是通过调研该设备所属机务专业主任,给定一个经验值;统计做法是通过统计或估算一段时间内该设备的累计实际工作时间(设备电路导通即视为工作状态)与载机累计飞行小时数的比值。前者给出的经验值受个人主观影响大;后者实际操作以来有些繁琐。现行方法的弊端是将运行比看作是一个定值,并没有考虑到设备工作时所处的环境因素(温度、振动和湿度等)对设备寿命的影响,即装备所处的地理气候环境、飞行载荷等对运行比的定量影响。
基于此,本文以设备实测工作时间为基础,考虑到地理气候环境、飞行载荷的影响,提出基于多因素影响程度的运行比确定模型,具体建模如下:

其中,

式中,分别为统计运行比权重、地理气候环境影响权重以及飞行载荷影响权重;为地理气候环境修正函数;为飞行载荷修正函数。计算公式如下:
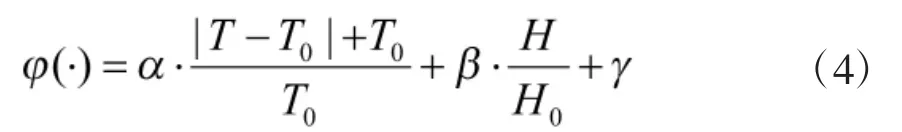
式中,T0表示基准地区的年平均气温;T为被评估对象所处地区的年平均气温;H0为基本地区的年平均空气湿度;H为被评估对象所处地区的年空气湿度;分别为温度应力、湿度应力以及其他(如盐雾、低气压、强紫外线灯)应力的经验系数。
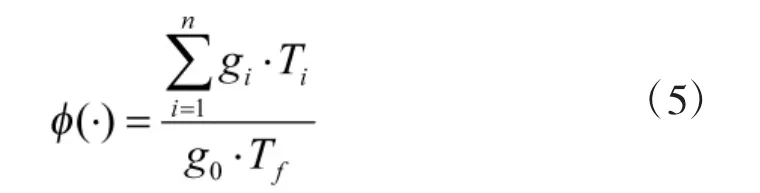
式中,g0表示基准的飞行载荷数;Tf为统计期间载机的累计飞行时间;gi表示统计期间第i个飞行科目/任务的经验载荷数;Ti为统计期间第i个飞行科目/任务的飞行时间;n为统计期间飞行科目/任务的总数。
3 完全修复件的外场可靠性评估模型
对于完全修复的设备级产品,可采用经典概率分布模型,针对具有随机截尾特征的所用参与统计的样本数据(包括:截止统计时刻未故障的样本数据和统计时间段内的故障数据和中途撤离样本数据),建立设备级产品外场可靠性评估模型。同时,对于不可修件故障前工作时间或可修件首次故障前工作时间(称为寿命),也可采用经典概率分布模型,求得寿命指标的估计值。
3.1 含随机截尾的经验分布函数
计算随机截尾的经验分布函数的方法有残存比率法、平均残存数法、平均秩法等,本文主要阐述其中较为常用的残存比率法。
将产品在时间上的残存概率S(ti)定义为:在时刻ti-1处于功能完好的产品能继续工作到时刻ti尚未故障的概率,用公式可表示为:
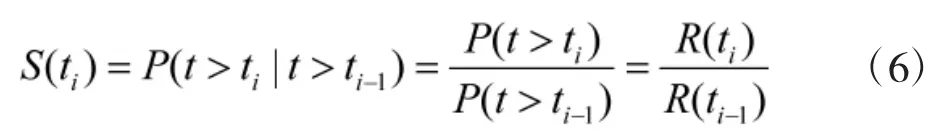
而残存概率S(ti)可通过数据样本的观测值估计出,公式为:
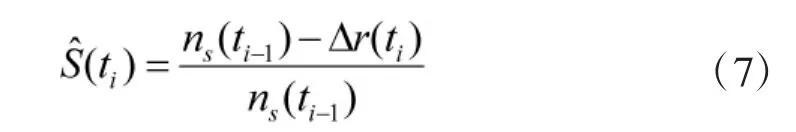
式中,为时间内的失效样本数;为在时刻ti-1继续处于功能完好的样本数。
时刻ti继续处于完好的样本数可表示为
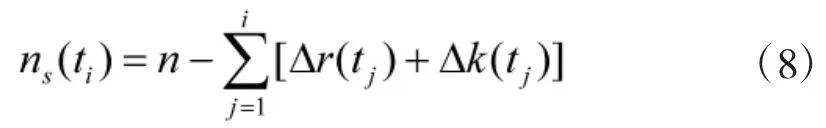
式中,n为试验样本总数;为时间内无故障中途撤离的样本数。
则在时刻ti产品经验可靠度和累积经验失效分布函数可表示为
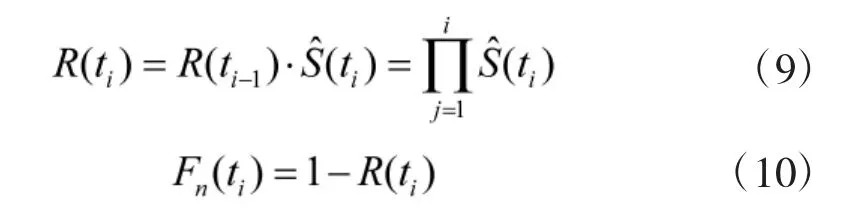
3.2 参数估计
计算出各时刻的经验分布函数值后,在相应的概率分布纸上描点连线,确定产品最佳的拟合分布类型,并通过拟合分布检验加以确认。主要为指数分布和威布尔分布
假设从上述分布的总体中随机选取n个样本作为试验样本量,采取定时截尾试验方式,时刻t0处结束试验,此时:有r个失效样本,失效时间为个中途撤离的样本,撤离时间为;有个未失效样本。
3.2.1 指数分布
设指数分布参数为,则未知参数的似然估计函数为:
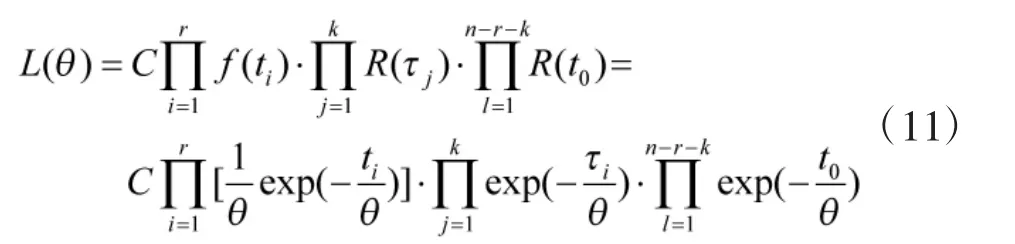
式中,C为多项式常数。
则未知参数θ(即平均寿命)的点估计值为:
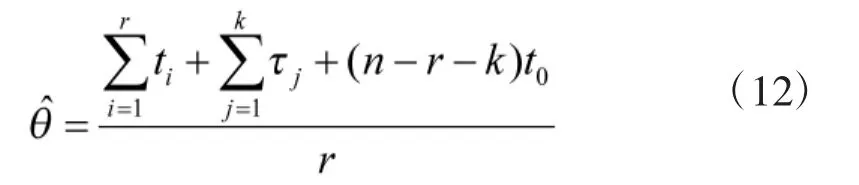
3.2.2 威布尔分布
设威布尔分布的分布参数为m,η,则未知参数的似然估计函数为:
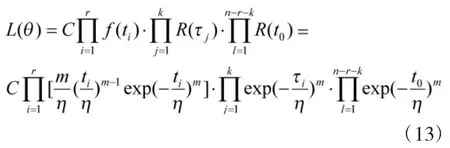
求解上述方程组即可求得未知参数m,η的估计值。当然也可以采用最小二乘法来求解未知参数估计。
平均寿命(MTBF)的点估计值为:
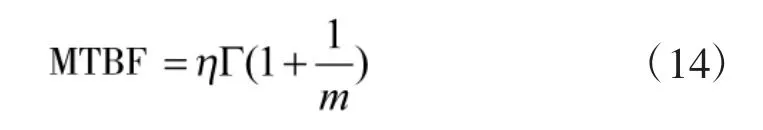
4 基本修复件的外场可靠性评估模型
对于基本修复的设备级产品,其修理前后的故障发生时间是相关的,一般假定其任意时间间隔内的故障数服从泊松过程,可采用非齐次泊松过程(NHPP)模型,只利用外场发生故障的样本数据,建立外场可靠性评估模型。
4.1 非齐次泊松过程
设(0,t]时间内产品发生故障的次数记为 N(t),这个随机过程记为且满足以下3个条件:
1);
2)有独立增量;
3)任意时间间隔内故障发生的次数服从参数为的泊松分布,即:
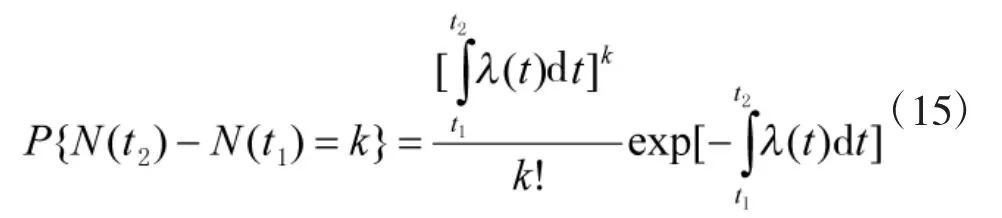
则称为非齐次泊松过程(NHPP)。
当NHPP中(成为故障强度)时,称此时的NHPP为威布尔过程(也就是AMSAA模型),则有:
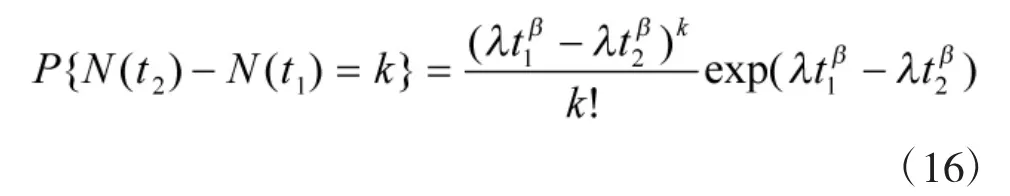
4.2 参数估计
4.2.1 单个基本可修产品
假设具有基本修复特性的某个航空产品在时间内共发生n个故障,故障时刻依次为,认为发生故障的次数符合威布尔过程,具有相互独立性,则有:
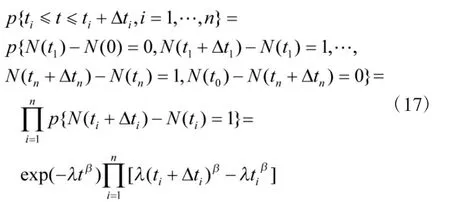
式中,△ti为充分小的时间变化量。
则服从威布尔过程的故障时刻的联合分布密度函数为:
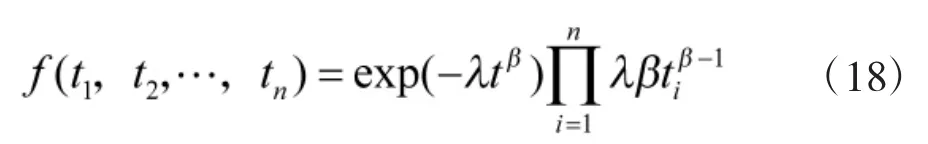
则未知参数的似然估计函数为:
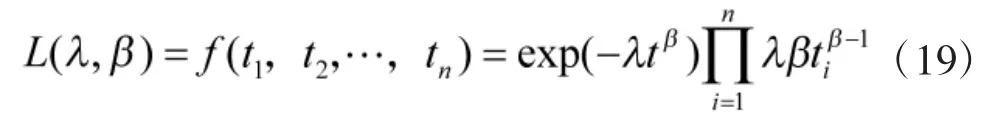
令上式关于的一阶偏导数为零,求得的估计值为:
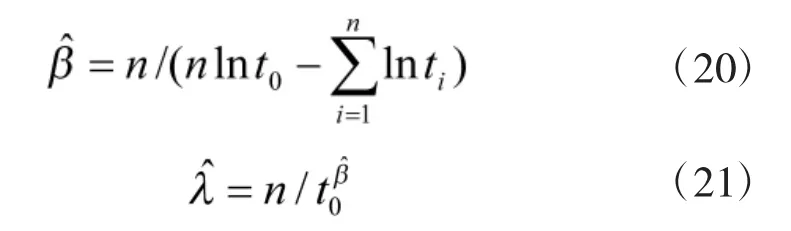
通过Cramer-von Mises拟合检验统计量为:
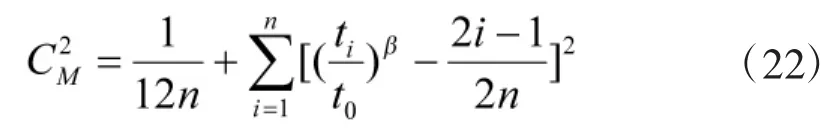
结果为接受,则认为发生故障的次数符合威布尔过程,则t0时刻产品的MTBF估计值为:
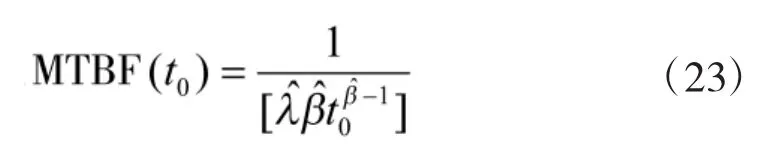
将产品从时刻t开始的任务时间段d内的任务可靠度Rt(d)定义为:在时刻内产品无故障的概率,可表示为:
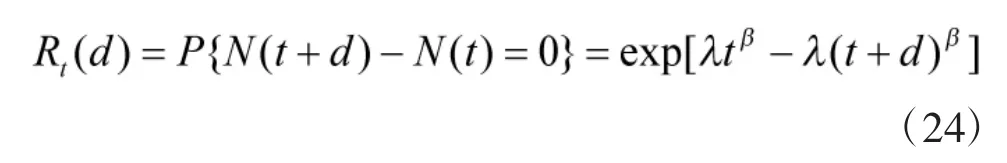
4.2.2 多个同型号基本可修产品
对于多个航空产品而言,在时间内第q个产品共发生个故障,则第q个产品第i个故障发生时刻为,且发生故障的次数符合威布尔过程,则未知参数的估计值可表示为:
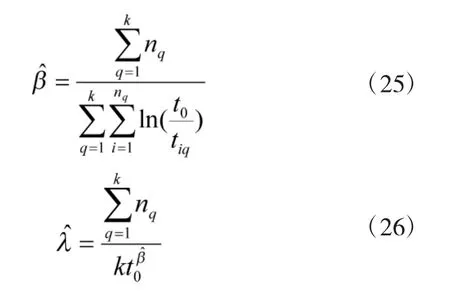
将所有故障时刻按照从小到大进行排序,得到新的故障时刻序列,则Cramer-von Mises拟合检验统计量可表示为:
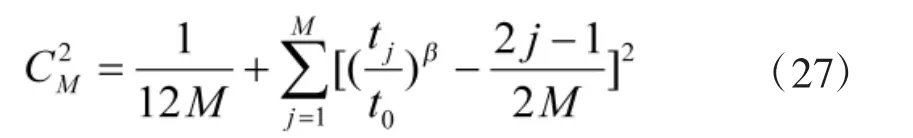
其中,

5 实例分析
5.1 完全修复件可靠性评估实例
某航空兵部队列装某型飞机24架,待评估的机载设备在飞机上的安装数为3个,现在收集到该部队单机外场500飞行小时内的该型设备的20个故障数据,按照故障发生时刻先后进行排序为21、35、100、128、150、152、205、264、288、290、311、321、330、334、346、350、411、476、479、499 (单位:h);中途撤离样本2个,撤离时刻分别为270、343(单位:h);故障时间缺失的故障样本有5个,经机务人员实测统计,得到该型机载设备的工作时间为385 h。
5.1.1 确定伪随机故障时间样本
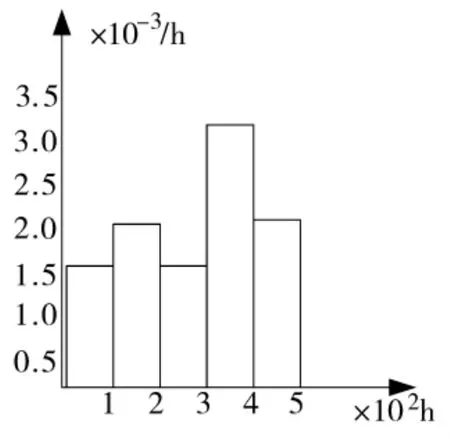
图1 故障频数直方图
采用随机数值模拟的方法,产生5个伪随机故障时间的样本。首先,绘制20个故障频数直方图,分组数为,组距,故障频数直方图见图1;然后,在图中直方图中按照均匀分布随机生成10组伪随机样本,取横坐标为伪随机样本的故障发生时刻,自助抽样结果如表1所示。
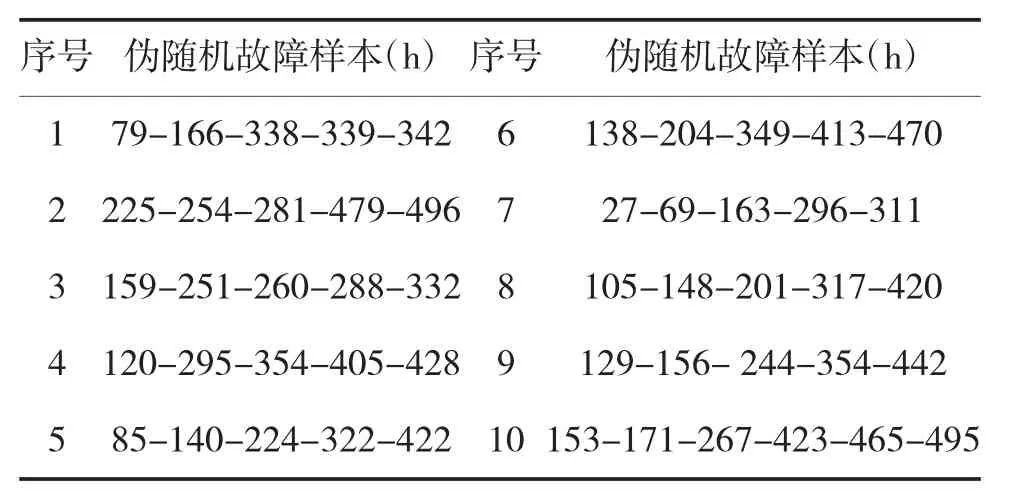
表1 10组伪随机故障样本
5.1.2 确定设备运行比确定模型
该部队驻地为广东湛江,属亚热带季风性气候,气候特点为高温高湿高盐雾,年平均气温为23℃,年平均相对湿度为82%,以年平均气温为15℃、年平均相对湿度为60%为基准值;温度、湿度以及其他(如盐雾、低气压、强紫外线灯)应力的经验系数分别取0.5、0.5、0.1;近年来,日常飞行科目训练向实战化聚焦,平均飞行过载达到2.5个g,以2个g为基准值;假设采用赋权方法,确定了统计运行比、地理气候环境、飞行载荷3个因素权重为0.452、0.256、0.292;采用基于多因素影响的运行比确定模型,由式(2)~ 式(5),计算出该型设备的运行比,如下:
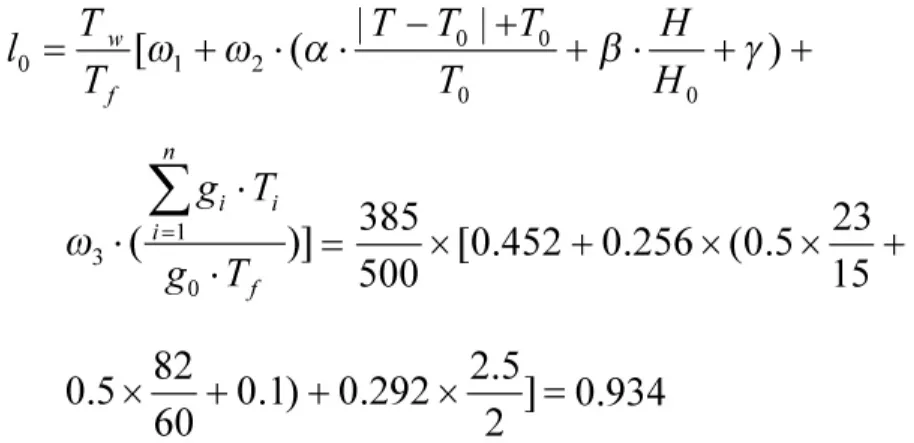
5.1.3 参数估计
假定该机载设备的总体寿命类型为威布尔分布,将产生的伪随机故障样本加入原有的20个故障样本中;用设备运行比(0.934),将样本的故障时刻(单位:飞行小时)转化为实际工作时间(单位:日历小时);由式(13),采用极大似然估计法,求得威布尔未知参数m,η的估计值见表2,则m,η的估计均值为:1.202、913;由式(14),算出 MTBF 为 726 h。
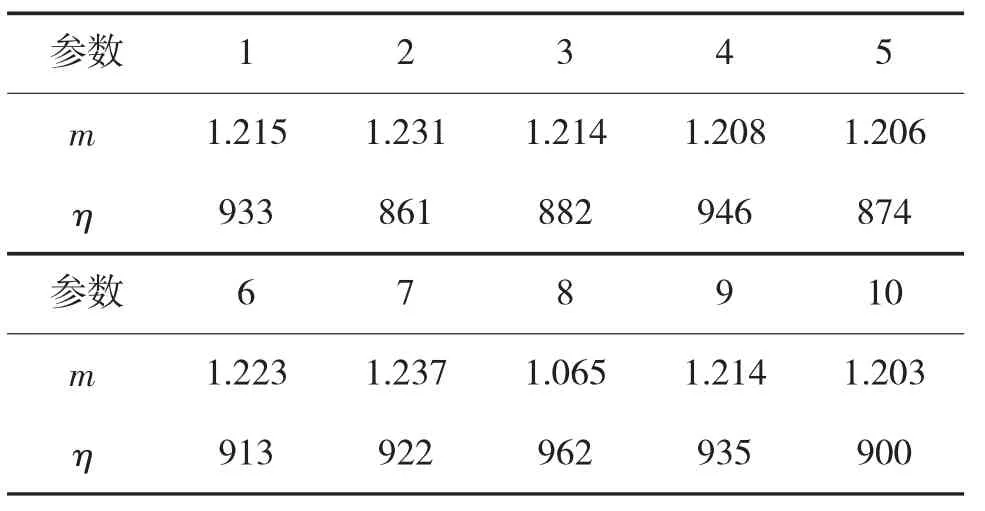
表2 10组分布参数估计值
5.2 基本修复件可靠性评估实例
若3个相同型号的航空产品在外场2000 h工作时间内的故障样本序列如图2所示(单位:h),其中:样本1故障9次、样本2故障11次、样本3故障13次。

图2 样本故障时刻序列图
根据式(25)、式(26),估计出威布尔过程参数为0.362和0.453,则故障强度函数为:,故障强度曲线如图3所示;由式(24)知,时刻t=0开始的任务时间d内的任务可靠度,任务可靠度曲线如53页图4所示。
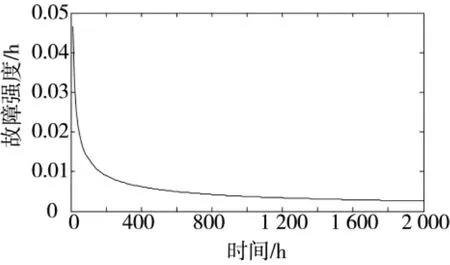
图3 样本故障强度曲线
根据式(27),计算出 Cramer-von Mises拟合检验统计量为;经查表,在显著水平α=0.10下,,都大于 0.053,结果表明接受上述故障样本符合威布尔过程模型的假设。
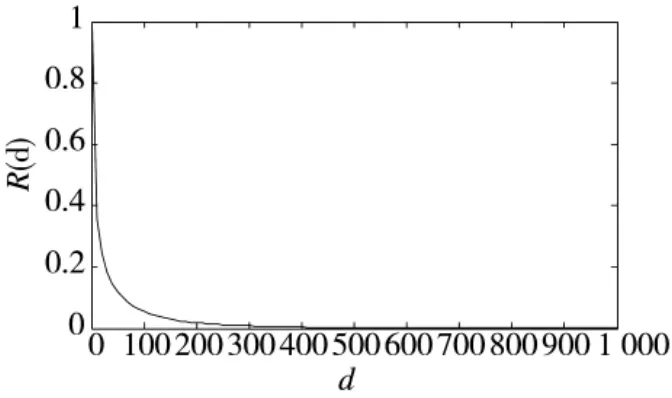
图4 t=0时的任务可靠度曲线
[1]中国空军百科全书编审委员会.中国空军百科全书[M].北京:航空工业出版社,2005.
[2]蔡忠义.多种应力试验下航空产品可靠性评估方法研究[D].西安:空军工程大学,2016.
[3]王星博,贾明明,于光辉,等.一种外场不完整故障数据的处理方法[J].航空计算技术,2011,41(6):80-84.
[4]张显余,付长安,王宏伟.基于故障信息流失情况下的一种可靠性评估法[J]. 空军航空大学学报,2008,1(5):26-29.
[5]陈云翔.可靠性与维修性工程[M].北京:国防工业出版社,2008.
[6]巨向斌,郑耀耀.电子系统和设备的外场可靠性评估[J].电光系统,2008,31(4):53-56.
[7]巨向斌,郑耀耀.电子设备定型阶段可靠性外场评估试验[J].电光系统,2008,31(3):59-63.
[8]崔毅勇,全成雨,丁利平,等.航空机载可修复产品外场可靠性评估模型及其应用[J].航空学报,2000,21(4):346-348.
[9]沈峥嵘,时钟.大型装备外场故障数据分析与可靠性评估方法[J].电子产品可靠性与环境试验,2012,30(6):29-34.
