同轴螺线管身管膛内电磁感应特性仿真与优化

毛保全 兰图 邓威

摘 要： 针对密绕螺线管在高频外部激励下感应磁场难以穿透金属圆筒壁的问题，基于麦克斯韦方程组推导不同激励类型的通电螺线管金属圆筒电磁感应特性，并以某型火炮身管为仿真算例，建立同轴螺线管身管电磁仿真模型，对不同激励频率下膛内电磁感应特性进行仿真分析。为进一步提高交流激励下膛内磁感应强度，以线圈参数、身管参数为设计变量，对同轴螺线管身管膛内电磁感应特性进行优化。仿真结果表明，膛内磁感应强度随着激励频率的提高呈指数型降低；在相同激勵条件下，可通过优化线圈、身管参数降低金属身管对外激励源的屏蔽效应，从而提高膛内等效磁场强度。

关键词： 螺线管； 身管； 电磁感应； 优化设计； 激励频率； 等效磁场强度

中图分类号： TN03?34； TP391.9 文献标识码： A 文章编号： 1004?373X（2018）11?0077?05

Simulation and optimization of electromagnetic induction characteristic

in chamber of coaxial solenoid′s barrel

MAO Baoquan， LAN Tu， DENG Wei

（Department of Weapon Engineering， Academy of Armored Force Engineering， Beijing 100072， China）

Abstract： Since the induction magnetic field of close?coiled solenoid is difficult to penetrate the metal cylinder wall under the high frequency external excitation， the electromagnetic induction characteristic of the metal cylinder of electrified solenoid with different excitation types is deduced on the basis of Maxwell′s equations， and the electromagnetic simulation model of the barrel of coaxial solenoid is established by taking a certain gun barrel as the simulation example to perform the simulation analysis of the electromagnetic induction characteristic in the chamber at different excitation frequencies. The coil parameter and barrel parameter are taken as the design variables to optimize the electromagnetic induction characteristic in the chamber of coaxial solenoid′s barrel， so as to further improve the magnetic induction intensity in the chamber at AC excitation. The simulation results show that the magnetic induction intensity is exponentially decreased with the increase of the excitation frequency； under the same excitation conditions， the optimization of coil and barrel parameter can reduce the shielding effect of the metal barrel on external excitation source， so as to improve the equivalent magnetic field strength in the chamber.

Keywords： solenoid； barrel； electromagnetic induction； optimization design； excitation frequency； equivalent magnetic field

0 引 言

施加磁场的圆筒腔体在军事领域有着广泛的应用，如励磁线圈火炮身管腔体产生的电磁场不仅能传递能量、提高身管发射弹丸的效能[1?2]，而且能传递信息、提高身管的可检测性[3]，目前，已在火炮身管缺陷检测、引信膛内感应储能、电磁线圈炮发射等领域得到成功应用。

身管的激励磁场可通过在身管上添加通电密绕螺线管实现。目前，关于螺线管的研究成果大部分集中在两方面：一方面是仅针对密绕螺线管的单独研究，主要研究螺线管的空间磁场分布特性[4?6]；另一方面是将螺线管应用于无损探伤领域，通过漏磁信号检测金属表面的缺陷[7?8]。然而，将螺线管与金属身管结合并着眼于膛内电磁感应特性的研究还鲜有报道。考虑到炮钢材质的火炮身管在电磁场中可等效为金属圆筒，在交变电流的激励下其表面形成的涡流场势必会削弱外激励磁场，从而对膛内等效磁场分布产生较大影响，因此，有必要对同轴螺线管身管膛内电磁感应特性进行研究。本文基于麦克斯韦基本理论推导不同激励类型下同轴螺线管身管膛内磁场分布数学模型，以某型身管为算例，利用Ansoft Maxwell建立密绕螺线管身管的电磁场数值仿真模型，并对不同外激励频率下身管内感应磁场进行仿真分析，其后固定激励条件不变，通过优化线圈参数及身管参数提高膛内磁感应强度。

1 螺线管金属圆筒电磁感应特性

1.1 通直流电螺线管金属筒内电磁感应特性

如图1所示为螺线管线圈结构简图，根据毕奥?萨伐尔定律，其单个载流圆环在空间任意点[P]产生的磁场为[9]：

[B=μ04πIdl×RR3] （1）

式中：[Idl]为圆环电流元；[R]为从电流元指向[P]点的矢量；[R]为电流元与[P]点间的距离；[ μ0]为真空磁导率；[B]为磁感应强度；[I]为线圈中的电流。[dl]，[R]，[R]分别由下列公式计算得出：

[dl=（-asinφi+acosφj）dφ] （2）

[R=（rsinθ-acosφ）i-asinφj+rcosθk] （3）

[R2=a2+r2-2arsinθcosφ] （4）

式中：[a]为载流圆环半径；[r]为[P]点到圆环圆心的距离；[θ]为[r]与[z]轴的夹角；[φ]为电流元与[x]轴的夹角。

当忽略电流的螺旋性以及线间距离时，可视为多个载流圆环的叠加。设螺线管长度为[2l]，线圈的匝数为[n]匝，则螺线管在[P]点产生的磁场为：

[B=nμ04π-lldzIdl×RR3] （5）

展开得：

当[xP=0]时，可得螺线管轴线处的磁场为：

[BzP=μ0nIa4π-lldz02πadφ（a2+（zP-z）2）3] （11）

螺线管轴向、径向磁场变化曲线分别如图2，图3所示。

螺旋管轴线处的磁感应强度在螺线管长度范围内缓慢变化，且关于[z=0]平面对称，在[z=0]处最强，在螺线管长度范围外磁感应强度迅速衰减；对于径向磁场变化情况，磁感应强度以螺线管中轴线为中心呈辐射对称分布，即磁场接近轴线处较强，距离轴线越远磁场强度越弱，在螺线管外部的磁场接近于零。

1.2 通交流电螺线管金属筒内电磁感应特性

当激励源为正弦电流时，螺线管中产生正弦变化的磁场，而变化的磁场将产生变化的涡流场，从而抵消原激励磁场的变化，对整体磁场的分布造成影响，此时磁场[B]和电场[E]可表示为：

[E=E0exp（-jωt）] （12）

[B=B0exp（-jωt）] （13）

考虑螺线管中有与螺线管半径相同的金属圆筒的情况，则金属导体会产生涡旋电流。由于涡旋电流远大于位移电流，故位移电流可忽略不计，可得：

[?2H0-jωγμH0=0] （14）

设螺线管线圈中交变电流角频率为[ω]，取柱坐标，设[k2=-jωγμ]，则[x=ky]，有：

[d2Hdx2+1xdHdx+H=0] （15）

式（5）为零阶Bessel方程，其解为：

[H=aJ0（kx）+bY0（kx）] （16）

式中：[J0（kx）]为第一类Bessel函数；[Y0（kx）]为第二类Bessel函数。

由于[H0]在[x=0]处为有限值，而[Y0（0）=∞]，因此，[b=0]，故：

[H0=aJ0（x）+aJ0（kr）] （17）

该问题的边界条件为：

[H（x）=H0R， r=R] （18）

[H0=H0RJ0（kR）J0（kr）] （19）

[k]为复数，在[J0（kr）]中展开，得：

[Her（v）≡ReJ0（i-12v）] （20）

[Hei（v）≡ImJ0（i-12v）] （21）

[J0（i-12r）≡Her（v）+jHei（v）] （22）

应用上述关系式，则：

[H（r）=H0Ber（rωμγ）+jBei（rωμγ）Ber（R2ωμγ）+jBei（R2ωμγ）] （23）

令[HH0=HH0<θ]，则有：

[H（r）H0=B2er（rrωμγ）+B2ei（rrωμγ）B2er（R2rωμγ）+B2ei（R2rωμγ）12] （24）

辐射角为：

[θ=arctanBer（rωμγ）Bei（R2ωμγ）-Ber（rωμγ）Bei（R2ωμγ）Ber（R2ωμγ）Bei（rωμγ）+Ber（R2ωμγ）Bei（rωμγ）] （25）

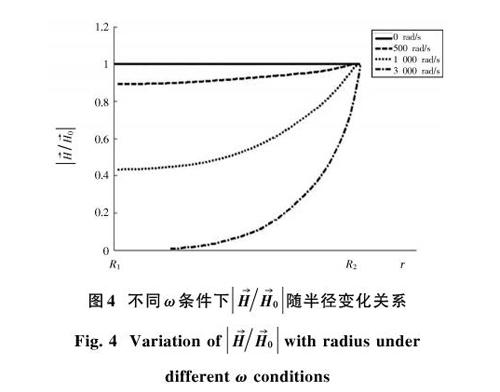
[HH0]为金属圆筒内磁场幅值与外激励磁场幅值的比值，其在不同[ω]条件下随半径变化的关系曲线如图4所示。

由图4可知，对于圆筒内部，[ω]越小，圆筒内部的磁场越接近均匀分布，随着[ω]的增大，金属圆筒内部的涡流场对外激励磁场的抵消作用越明显。通过不同[ω]条件下磁感应仿真曲线可以得出，当[ω]=3 000 rad/s时，在圆筒中心的磁场强度接近于零，此时[ω]外激励磁场的谐振频率为573 Hz。

2 同轴螺线管身管膛内电磁感应特性

2.1 仿真模型的建立

以某型火炮身管為仿真算例，通过Maxwell构建火炮身管模型及密绕线圈模型，以研究火炮身管加装线圈后的电磁效应。为提高仿真效率，火炮身管通过金属圆筒进行模拟，圆筒壁外密绕线圈形成螺线管，在Maxwell中建立外套密绕螺线管的火炮身管简化模型，如图5所示。

图5中，外部环状为励磁线圈，内部圆筒为身管等效模型。模型中圆筒长度为600 mm，外径及内径分别为40 mm，30 mm，；螺线管通过winding功能添加于身管外壁，位于孔长度的中间位置，其内径为35 mm；线圈外径为50 mm，内径为40 mm，长度为300 mm；身管材料选用PCrNi3MoVA钢，螺线管材料设置为铜；激励设置于身管横截面上。

2.2 结果分析

激励和边界条件设置完毕后进行求解计算，得到模型的磁场强度矢量图、磁力线图及磁场强度分布图，如图6，图7所示。

由图6，图7可以看出，螺线管激励磁场主要集中在螺线管内部，在螺线管外部的磁感应强度较低；外激励在圆筒引发的涡流场反作用于外激励，大幅度削弱了螺线管内部的磁感应强度，导致磁场仅存在于金属圆筒壁。以上结论表明，金属圆筒的存在较大程度地改变了螺线管的空间磁场构型，大大削弱了螺线管内部的磁场强度，上述仿真结果进一步验证了前述小节理论分析的正确性。

2.3 不同激励频率对膛内电磁感应特性的影响

为进一步掌握不同外激励频率下螺线管金属圆筒的磁感应特性，分别以0，100 Hz，200 Hz，300 Hz，500 Hz等不同激励频率进行仿真，结果如图8所示。

由圖8可知，当外激励频率为0时，圆筒腔体内部感应磁场沿轴线均匀分布，在圆筒端部迅速衰减；当外激励频率不为0时，圆筒内部等效磁场随外激励频率的提高而减弱，当外激励频率为100 Hz时，穿透金属圆筒至轴线处的磁场强度为激励磁场强度的61.9%，而激励频率达到500 Hz时，穿透后的磁场仅为激励磁场强度的3.4%。

3 螺线管身管膛内电磁感应特性优化

为进一步提高螺线管在身管内部的激励磁场强度，以线圈参数及身管参数为设计变量，对同轴螺线管金属筒内电磁感应特性进行优化。线圈参数包括线圈密度、匝数及厚度，身管参数包括磁导率及电导率。通过优化设计变量来提高轴线处磁场强度，优化效果则可通过其与外激励磁场强度的比值与基准值的比较进行量化表征。

3.1 优化模型

根据上述仿真结果，以交变电流激励下穿透金属圆筒至轴线处的磁场强度为激励磁场强度的50%作为基准穿透比例，其对应的线圈、身管参数作为初始条件，设计变量及取值范围如表1所示。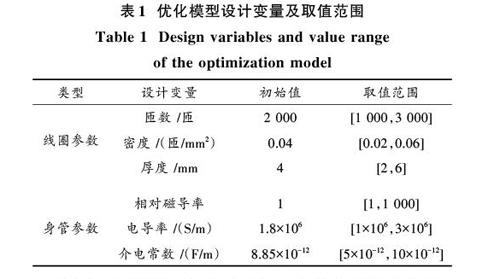

同时，选择螺线管激励磁场与身管轴线处磁场的比值与基准值（50%）的变化幅度作为表征电磁感应特性优化效果的特征量。

[F=HmH0-0.50.5×100%] （26）

3.2 优化算法

考虑到遗传算法具有发展成熟、收敛速度快、不易陷入局部最优解等优点[10]，因此，选择其作为本文的优化算法。遗传算法将每个可行解等同于生物学个体，优化前系统随机将[N]个个体组成初始种群，然后人为确定适应度函数，系统则根据适应度高低对个体进行排序，并将其中高适应度的个体进行遗传操作（选择、交叉及变异），对低适应度的个体进行淘汰。该过程反复进行，直至最终适应度最好的个体被筛选出来，即为全局最优解。寻优过程如图9所示。

在本文仿真分析中，种群数量设置为44，交叉概率及变异概率分别为0.65，0.04，收敛阈值为0.01。

3.3 优化计算与结果分析

对上述同轴螺线管身管膛内电磁感应特性优化设计进行仿真计算，结果如图10，表2所示。

由图10可知，优化过程经过732次迭代后收敛到全局最优解。由表2可知，全局最优解为匝数1 769匝，密度0.03匝/mm2，厚度5.04 mm，相对磁导率712，电导率1.44×106 S/m，介电常数7.25×10-12 F/m，表明在该最优参数组合下，同轴螺线管身管膛内轴线处磁场强度为外激励磁场强度的63%，相比初始值优化幅度为26%，优化效果较为显著。

4 结 论

通过本文研究可得出如下结论：

1） 金属圆筒在交变电流的激励下会产生涡流，削弱外激励穿透至金属圆筒的磁场强度，从而对外部磁场产生屏蔽效应。

2） 金属身管对同轴螺线管激励磁场的屏蔽效应随着激励频率的增加而剧烈，穿透后的磁场强度随频率的提高而呈指数规律衰减。仿真结果表明，若使穿透后的磁场强度不小于激励磁场强度的61.9%，需将外激励频率控制在100 Hz以下。

3） 在相同激励条件下，通过优化线圈参数及身管参数，能够使同轴螺线管身管膛内磁场强度得到提高，对于轴线磁场强度为外激励磁场强度50%的原有激励条件，通过调节身管参数及线圈参数，能够使该穿透比例优化至63%。

参考文献

[1] 李军，严萍，袁伟群.电磁轨道炮发射技术的发展与现状[J].高电压技术，2014，40（4）：1052?1064.

LI Jun， YAN Ping， YUAN Weiqun. Electromagnetic gun technology and its development [J]. High voltage engineering， 2014， 40（4）： 1052?1064.

[2] 吴志亮，张合.小口径引信膛内感应储能磁场穿透特性[J].兵工学报，2010，31（10）：1310?1315.

WU Zhiliang， ZHANG He. The magnetic field penetration characteristics in bore of small caliber fuze using inductive energy [J]. Acta armamentarii， 2010， 31（10）： 1310?1315.

[3] 郭希玲.交变漏磁检测技术及螺纹缺陷识别的研究[D].长沙：国防科学技术大学，2005.

GUO Xiling. Research on technology of alternative current magnetic field leakage and flaw identification to the whorl [D]. Changsha： National University of Defense Technology， 2005.

[4] 冯涛.有限长螺线管场分布特性分析[D].西安：西安电子科技大学，2013.

FENG Tao. Analysis on field distribution characteristics of limited solenoid [D]. Xian： Xidian University， 2013.

[5] 廖斌，邓春凤，吴先映，等.利用Matlab计算螺线管内磁场分布研究[J].北京师范大学学报（自然科学版），2010，46（6）：688?690.

LIAO Bin， DENG Chunfeng， WU Xianying， et al. Inner magnetic field distribution of solenoid studied by Matlab [J]. Journal of Beijing Normal University （natural science）， 2010， 46（6）： 688?690.

[6] 蔡伟，伍樊成，杨志勇，等.基于麦克斯韦方程的交变电流长螺线管磁场[J].强激光与粒子束，2015，27（12）：162?167.

CAI Wei， WU Fancheng， YANG Zhiyong， et al. Analysis of solenoid magnetic field based on Maxwell equation [J]. High power laser and particle beams， 2015， 27（12）： 162?167.

[7] 黄平.低频电磁技术在储罐罐底缺陷检测中的应用研究[D].沈阳：沈阳工业大学，2016.

HUANG Ping. Application research of low frequency electromagnetic technology in defect detection of tank bottom [D]. Shenyang： Shenyang University of Technology， 2016.

[8] 吳德会，游德海，柳振凉，等.交流漏磁检测法趋肤深度的机理与实验研究[J].仪器仪表学报， 2014，35（2）：327?336.

WU Dehui， YOU Dehai， LIU Zhenliang， et al. Mechanism and experimental research on skin depth in AC magnetic flux leakage testing [J]. Chinese journal of scientific instrument， 2014， 35（2）： 327?336.

[9] 蔡旭红，李邵辉.有限长通电螺线管内部空间磁场的模拟[J].汕头大学学报（自然科学版），2004（2）：28?31.

CAI Xuhong， LI Shaohui. Simulation for spatial magnetic field distribution in a finite solenoid [J]. Journal of Shantou University （natural science）， 2004（2）： 28?31.

[10] 梁传建，杨国来，王晓锋.基于神经网络和遗传算法的火炮结构动力学优化[J].兵工学报，2015，36（5）：789?794.

LIANG Chuanjian， YANG Guolai， WANG Xiaofeng. Structural dynamics optimization of gun based on neural networks and genetic algorithms [J]. Acta armamentarii， 2015， 36（5）： 789?794.