改进灰狼优化算法在WSN节点部署中的应用*

胡小平,曹 敬

(湖南科技大学先进矿山装备教育部工程研究中心,湖南 湘潭 411201)

无线传感网络是由一定规模的终端传感节点通过无线通信的方式组成的一种自组织网络。传感器节点通常具有通信、计算、感知等能力,通过对其规模化部署形成的无线传感网络具有对监测区域进行监控的能力。无线传感网络中单个节点仅承担部分检测任务,单个节点故障对网络的整体监测能力影响较小,且节点之间进行无线通信无需要人工铺设线缆拥有更好的连接便利性。因此,通过大量节点部署后组织的无线传感网络拥有良好的容错能力和断接性能等特点。近年来,无线传感网络广泛运用于辅助农业生产、环境监测、物流和智能家电领域。在应用过程中,传感器节点多采取随机抛洒的部署方式,由于部署位置随机,使其存在覆盖盲区,难以有效覆盖待监测区域,从而影响网络的监控能力。监测区域环境变化和传感器节点可移动性改变等因素会降低网络覆盖率从而影响其监控能力。因此,需要对无线传感网中传感器节点的进行自适应的调整部署,以于提高传感网络覆盖率、减少覆盖盲区、减少传感器部署数量以节约网络构建成本[1-2]。

近几年来,灰狼优化算法GWO(Grey Wolf Optimizer)得到了广泛关注。灰狼优化算法是由学者Mirjalili等人于2014年提出了一种新的群智能算法,文献[3]表明,在基准函数求解问题上,GWO算法与粒子群算法PSO(Particle Swarm Optimization)算法、(差分进化算法DE(Differential Evolution)算法和万有引力算法GSA(Gravitational Search Algorithm)算法相比拥有更高的精度和稳定性。国内外学者对灰狼优化算法进行了大量的研究:姚鹏等人将灰狼优化算法与流体扰动算法结合应用于无人机三维航路规划得到了平滑性和可飞性高的三维航路[4];Sulaiman等人研究了灰狼算法在最优无功电力调度问题上的应用,表明与其他技术相比灰狼算法能实现更小的功率损耗和电压偏差[5];Madadi等人利用灰狼优化算法对直流电机PID控制器参数进行优化,相比PSO算法提高了控制的稳定性[6];Song等人将GWO应用于表面波色散曲线反演,与遗传算法相比GWO算法减少了控制参数的同时提高了收敛速度[7];HM Song将灰狼优化算法引入电力系统的组合经济排放调度问题,以此得到了最佳的发电方式[8];Mahdad等人将灰狼优化算法应用于电力控制系统以减小停电风险,通过实际测试证明了该方法的安全性和可行性[9];针对在应用过程中灰狼优化算法出现的中后期收敛速度慢和易陷入局部极值的问题。Nasrabadi 等人通过并行和反向学习改进灰狼优化算法,提高了算法在解决基准函数求解问题上的速度和精度[10];郭振洲等人将非线性收敛因子与动态权重引入灰狼优化算法,加快了算法收敛速度[11];徐松金等人利用佳点集理论初始化种群,在迭代过程中引入算术交叉和多样性变异操作以避免算法陷入局部最优解并增强算法的局部搜索能力,其改进算法在较高维度函数求解问题上对比标准灰狼优化算法拥有明显优势[12]。

标准灰狼优化算法在应用于优化问题时存在中后期收敛速度慢且容易陷入局部极值问题[13]。文献[14]认为,提高初始种群的多样性有助于提高搜索算法的搜索效率。而混沌算法具非线性系统的特点,具有非重复性与遍历性的特点。混沌算法引入种群初始化,利用其特点生成初始种群以提高初始种群多样性,为全局搜索提供基础;此外,使用改进的非线性收敛因子代替标准灰狼优化算法中的线性收敛因子,以提高算法中后期的搜索能力加快收敛速度;最后,对第三优解进行融合变异,以加快搜索速度和避免陷入局部最优解。并将改进灰狼优化算法应用于无线传感网络节点部署问题,开展改进算法的仿真分析。

1 节点与覆盖模型

(1)

任一目标点可以被多个传感节点同时检测,则对目标点的联合测量概率为:

(2)

式中:gov为测量目标点的传感器集合。所有节点对待检测区域的覆盖率为:

(3)

式(3)覆盖率函数值的最大化为无线传感网络覆盖模型的优化目标。

若无线传感网络中的两节点间距离不大于通信半径,则认为两节点间存在一条通信路径。定义Hij为任意两节点i与j之间的通信路径数量。满足网络连通要求的约束为:Hij≥1。同时,所有的节点位置应处于待监测目标区域内,可表示为:L(gi)∈M。

综上所述目标函数为:

(4)

2 灰狼优化算法基本原理

灰狼优化算法是一种启发式算法,其通过模拟自然界中灰狼群的等级划分以及狩猎机制达到逼近目标的目的。根据简化的灰狼的社会层次结构数学模型,灰狼个体被划为4个类型:α、β、δ、ω。其中头狼α狼为当前最优解,β狼为当前次优解,δ狼为当前第三优解,ω狼为其余的备选解。为描述灰狼在包围猎物过程提出的数学模型为:

D=|C·Xp(t)-X(t)|

(5)

X(t+1)=Xp(t)-A·D

(6)

式中:D为个体与目标之间的距离,t为当前迭代次数,C和A为系数向量,Xp为目标位置向量,X为单只灰狼位置向量。C和A计算公式为:

A=2ar1-a

(7)

C=2r2

(8)

式中:r1,r2表示[0,1]间的随机数,收敛因子a随迭代次数增加从2线性减小到0:

a=2-2t/tmax

(9)

式中:tmax为最大迭代次数。

自然界中的灰狼拥有判断目标位置和包围猎物的能力。而在实际的函数优化过程中目标位置是不可知的。在实际应用中,通过计算每个灰狼对目标函数的适应度,选取灰狼种群中适应度前三的个体:α狼、β狼和δ狼,并由其指引狼群搜索方向,对目标位置进行搜索。通过多次灰狼的位置更新逐渐逼近目标位置。其数学描述如下:

Dα=|C1Xα-X|

(10)

Dβ=|C2Xβ-X|

(11)

Dδ=|C3Xδ-X|

(12)

X1=Xα-ADα

(13)

X2=Xβ-ADβ

(14)

X3=Xδ-ADδ

(15)

X(t+1)=(X1+X2+X3)/3

(16)

根据式(15)对灰狼个体进行更新。

3 改进灰狼优化算法

3.1 混沌初始化

混沌是一种确定的、随机的非线性动力系统,具有非周期性、不收敛和有界的特点。自上个世纪以来混沌映射在优化算法领域得到了广泛的重视。因为其动态随机特性,能使优化算法在搜索区域进行更有效的的全局搜索。

John Wiley[12]等人认为较高的初始种群多样性能提高启发式搜索算法的搜索效率。在全局最优解未知的情况下,将初始种群尽可能遍布在搜索范围内,能为算法前期提供良好全局搜索基础。尽管标准灰狼优化算法具有较好的收敛速度,但在解决全局最优问题时随机产生的初始种群可能导致多样性较差,影响算法的全局搜索能力,出现收敛速度较慢或者收敛精度不理想的情况。为了提高算法搜索效率,将混沌映射引入灰狼算法的初始化中,通过混沌映射使初始个体均匀的分布在搜索区域内,提高初始化种群的多样性。在混沌映射模型的选择上,本文采用较为常用的Logistic映射模型进行算法种群的初始化。数学描述如下[13]:

(17)

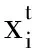
(18)

式中:j=1,2,…,m为种群序号;[ai,bi]为Xi的搜索范围。

3.2 非线性收敛因子

启发式算法在需要在搜索能力和开发能力之间保持良好的平衡,从而实现有效的全局和局部搜索。搜索能力即寻找新的适应度更高的个体的能力;开发能力即为在当前最优解位置附近寻找更优的解的能力。

在标准灰狼优化算法中,收敛因子a的自适应值起到平衡搜索能力和开发能力的作用。算法初期较大的a值保证全局搜索能力。随着迭代次数的增加a的值逐渐减小,从而加强在当前最优解附近搜索的能力。文献[11]表明,GWO算法根据A的绝对值进行搜索能力与开发能力的调节,当A绝对值大于1时,灰狼个体将扩大搜索范围进行全局搜索;反之灰狼个体将缩小搜索范围进行局部搜索。由式(6)可知A的值由收敛因子与系数决定。在复杂的算法搜索过程中,标准灰狼优化算法从2到0线性减小的收敛因子不能完全平衡算法搜索过程中的搜索能力和开发能力。为了提升算法搜索精度和速度,改进的灰狼优化算法,其收敛因子随迭代次数增加呈非线性变化,表达式如下:

(19)

式中:ainitial为a给定的初始值;常数μ为非线性调节系数;常数k的值影响算法搜索和开发能力,k值越小则在最优解附近搜索新的最优解能力越强。实际应用中,可根据具体优化问题,调节收敛因子相关系数从而平衡算法搜索能力与开发能力,提高算法搜索效率。

3.3 δ狼的融合变异

标准灰狼优化算法在中后期主要由前三优的解引导搜索方向。若这3个解陷入局部极值,则容易导致最优解的更新停滞从而出现算法过早收敛。为改善过早收敛问题,在一定概率下将δ与α和β的进行融合变异,产生新的δ狼。将第三优解与适应度更高的两个解进行融合变异,更容易得到比当前第三优解适应度高的解,并将其取代当前第三优解。以此加快δ狼更新,从而影响其余个体搜索方向,改善算法陷入局部极值的情况同时也能加快算法搜索速度。以D的概率对δ狼中的第j维进行融合变异,过程如下:

(20)

式中:j=1,2,…,n为维度序号,υ1、υ2、υ3为[0,1]的随机数且υ1+υ2+υ3=1。

4 节点部署优化算法

本文算法以无线传感网络覆盖模型中覆盖率最大化为优化目标,利用一定的数量的传感节点实现对检测区域覆盖率的最大化。算法中灰狼种群包含多灰狼个体,每个灰狼个体拥有相同的维度数,均代表所有传感节点的一种覆盖分布方式。待测区域为二维平面,则灰狼个体的维度数为传感节点数的两倍,其中第2i和第2i-1维分别为第i个传感节点的横坐标和纵坐标。算法优化结束后输出算法优化过程中搜索到的适应度最好的一个解,得到所有传感节点优化部署后的分布位置。

4.1 算法步骤

Step 1 设置算法a、A、C等参数,种群规模m,迭代次数t。

Step 2 根据3.1节所述方法对初始种群进行混沌初始化,设t=1。

Step 3 计算初始群体中每个灰狼个体的适应度值,选取适应度值前三的个体并分别设置为Xα、Xβ和Xδ。

Step 4 由式(15)更新每个灰狼位置。

Step 5 计算种群每个灰狼适应度值,并更新Xα、Xβ和Xδ。

Step 6 根据3.3所述对δ狼进行融合变异。

Step 7 根据式(18)更新a的值,根据式(6)和式(7)更新A和C的值。

Step 8 判断是否满足算法结束条件。若不 满足,则t=t+1,返回Step 4;若满足,则算法结束,输出Xα。

4.2 算法流程图

根据上述内容,IGWO可应用于WSN节点部署中的覆盖率优化问题。以式(4)为目标函数进行优化,可得到满足各约束条件的覆盖优化后的各节点分布位置。

具体流程如图1所示。

图1 IGWO覆盖优化流程图

5 仿真实验与分析

假设在面积S=50 m×50 m的待检测区域。所有传感节测量半径为r=5 m,通讯半径为rs=15 m,最大迭代次数tmax=100,其余参数设置为ainitial=2,μ=10,k=4,D=0.15。实验中40个无线传感节点均为移动传感节点。使用MATLAB在主频为2.3 GHz的PC机上进行无线传感网络优化部署仿真。

图2 最大迭代次数与覆盖率

图2为采用初始随机抛撒后,标准算法灰狼优化算法与改进灰狼优化算法的进行覆盖优化后的覆盖率对比图。经两种算法优化后的节点覆盖率较初始部署覆盖率均有大幅提高。节点数量为70时,IGWO优化算法与GWO算法均能使覆盖率接近100%。在节点数量为40时,IGWO算法对目标区域的覆盖率与GWO算法的覆盖率差值较大。在目标区域内抛撒40个传感器节点,分别采用标准灰狼优化算法和改进灰狼优化算对无线传感网节点部署进行优化后的结果如图4和图5所示,优化用时分别为:147.7 s和158.6 s,改进后灰狼优化算法优化用时增加主要为算法种群初始化计算用时增加,改进后灰狼优化算法在一定程度上提高了算法复杂度。两者对待测区域覆盖率分别为91.16%,94.28%,改进灰狼算法对比标准灰狼优化算法覆盖率提升了3.12%。节点在待测区域内分布更加均匀,改善了部分区域节点聚集过于的情况。改进灰狼优化算法与标准灰狼优化算法相比在收敛速度上也得到了提升,如图6所示。

图6 算法优化后覆盖率对比

图3 初始部署

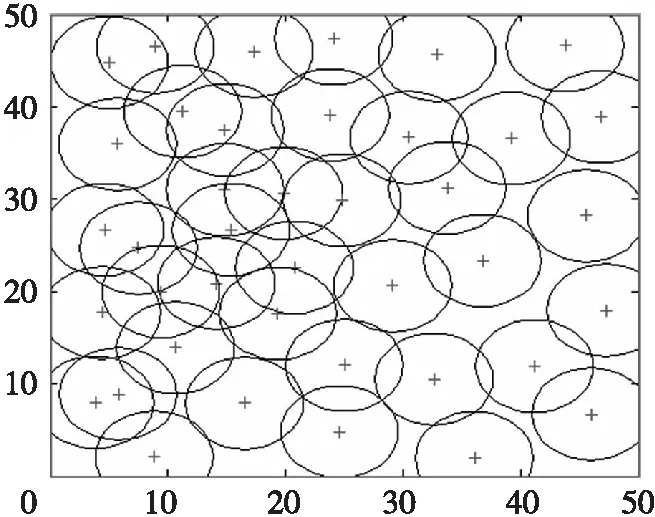
图4 GWO优化覆盖

图5 IGWO优化覆盖

上述仿真实验结果表明,改进灰狼优化算法应用适应性强,收敛速度快。应用于无线传感网络节点部署优化问题,能快速有效的提升网络覆盖率,减少覆盖盲区。在同样的覆盖率要求下,所需节点数量较少,能降低网络构建成本。

6 结束语

本文在标准灰狼优化算法的基础上,使用混沌映射进行种群初始化提高灰狼种群多样性以加强算法全局搜索能力;利用改进的非线性收敛因子以平衡算法的搜索和开发能力;将第三优解进行融合变异以减小算法陷入局部最优的可能。并将改进灰狼优化算法应用于WSN的覆盖优化问题中。仿真实验结果表明,改进后的灰狼优化算法能在一定程度上提高无线传感网络性能。在应用过程中出现算法优化结果不稳定的现象,今后的研究方向应进一步提高算法稳定性,并将在综合考虑网络节点移动距离与环境因素的前提下完成传感器节点部署。

参考文献:

[1] Wang Y,Wang R C,Cheng X. Improved Multipath Routing with WNN for the Open Networks[J]. 中国邮电高校学报(英文版),2008,15(2):107-113.

[2] 吴意乐,何庆,徐同伟. 改进自适应粒子群算法在WSN覆盖优化中的应用[J]. 传感技术学报,2016,29(4):559-565.

[3] Mirjalili S,Mirjalili S M,Lewis A. Grey Wolf Optimizer[J]. Advances in Engineering Software,2014,69(3):46-61.

[4] 姚鹏,王宏伦. 基于改进流体扰动算法与灰狼优化的无人机三维航路规划[J]. 控制与决策,2016,31(4):701-708.

[5] Sulaiman M H,Mustaffa Z,Mohamed M R,et al. Using the Grey Wolf Optimizer for Solving Optimal Reactive Power Dispatch Problem[J]. Applied Soft Computing,2015,32(C):286-292.

[6] Madadi A,Motlagh M. Optimal Control of DC Motor Using Grey Wolf Optimizer Algorithm[J]. Technical Journal of Engineering and Applied Science,2014,4(4):373-379.

[7] Song X,Tang L,Zhao S,et al. Grey Wolf Optimizer for Parameter Estimation in Surface Waves[J]. Soil Dynamics and Earthquake Engineering,2015,75:147-157.

[8] Song H M,Sulaiman M H,Mohamed M R. An Application of Grey Wolf Optimizer for solving combined economic emission dispatch Problems[J]. International Review on Modelling and Simulations,2014,7(5):838-844.

[9] Mahdad B,Srairi K. Blackout Risk Prevention in a Smart Grid Based Flexible Optimal Strategy Using Grey Wolf-Pattern Search Algorithms[J]. Energy Conversion and Management,2015,98:411-429.

[10] Nasrabadi M S,Sharafi Y,Tayari M. A Parallel Grey Wolf Optimizer Combined with Opposition Based Learning[C]//Swarm Intelligence and Evolutionary Computation. IEEE,2016:18-23.

[11] 郭振洲,刘然,拱长青. 基于灰狼算法的改进研究[J]. 计算机应用研究,2017(12):1-8.

[12] Haupt R,Haupt S. Practical Genetic Algorithm[M]. New York:John Wiley and Sons,2004:38-39.

[13] Ragulskis M,Vainoras A,Smidtaite R,et al. The Logistic Map of Matrices[J]. Discrete and Continuous Dynamical Systems-Series B(DCDS-B),2017,16(3):927-944.