一种基于多属性单值中智集相关度量测的视频运动目标检测方法*

胡珂立,范 恩,叶 军,樊长兴,沈士根,谷宇章

(1.绍兴文理学院计算机科学与工程系,浙江 绍兴 312000;2.绍兴文理学院电子与信息工程系,浙江 绍兴 312000;3.中国科学院上海微系统与信息技术研究所,上海 200050)

伴随着平安城市、平安社区的进一步建设以及视觉传感器件的不断发展,视觉分析仍是当前最为重要的环境感知手段之一。视频运动目标检测[1,2]是进行后续高级视觉分析任务的重要基础,其效果很大程度上决定着后续分析的优劣。视频运动目标检测的任务即为将运动目标(前景)从静态信息(背景)中分离出来,因此,运动目标检测也称前景检测。

背景差方法经常被用于前景分离,近年来众多研究者针对该类方法进行了深化研究。文献[3]将混合高斯模型用于运动目标检测,算法为图像中的每个像素点都建立相应的混合高斯模型,并进行在线更新。鉴于混合高斯前景检测方法的有效性,多项旨在提升传统混合高斯模型检测方法的众多方法被相继提出[2,4-7]。文献[6]结合目标帧间相关性和随机噪声帧间无关的特性对混合高斯模型结果进行了优化,文献[7]采用增量式主成分分析来建立特征基背景模型。对于视频监控,一些不准确或不确定的信息通常会在背景差分的过程中被带入。模糊理论被引入到动目标检测中[8]。在文献[9]中,模糊模型被用来解决前景检测过程中的决策问题。在文献[10]中,作者基于Type-2模糊高斯混合模型和马尔科夫随机场提出了一种针对动态场景的背景建模方法。这种方法能较好的应对画面中摇晃的树叶和水面的波纹。文献[8]给出了模糊理论用于背景差动目标检测的综述。

相较于传统的模糊理论,中智集理论[11]除了对真(Truth)、假(Falsity)分量进行表述外,还专门对不确定(Indeterminacy)分量进行了处理。中智集理论在处理不确定信息方面展现出了很好的表现,因此被广泛用于计算机视觉[12-18]、汽轮机故障诊断[19]、治疗方案选择[20,21]、聚类理论等[12,13,22,23]。文献[12]提出了中智相似聚类方法,并将该方法成功用于图像分割。文献[13]将中智集和模糊C均值聚类用于改进肝脏CT图像分割。这之后,为了改进C均值聚类,文献[22,23]将不确定因素考虑进来,提出了基于中智集的C均值聚类方法。除此以外,文献[14]将不确定滤波器引入图像分割。在文献[15]中,单值中智交叉熵被用来融合颜色域和深度域信息。在文献[18]中,单值中智集余弦相似度量测被用来融合目标区域和背景区域信息。文献[21]首次提出多时段单值中智集相关度量测,并成功用于医疗诊断。对于中智集理论在图像分割上的应用[12-17],研究者通常会在分割之前建立一张特定的中智图像,用以对抗图像噪声的干扰。在文献[17]中,多个中智特征属性被提出来并用于计算静态图像分割阈值。在目标图像中存在较严重的噪声干扰时,该方法表现出了较好的稳定性。尽管目前已提出了较多的基于中智集的图像分割方法,但已有方法均是针对静态图像的分割。对于运动目标检测而言,除了帧内信息外,帧间关联信息对目标提取及抗噪尤为重要。因此,鉴于中智集在处理不确定信息时表现出的优越性,将中智集理论引入运动目标检测中以解决外部挑战带来的噪声干扰问题是非常有意义的。

本文首次将多时段单值中智集应用于视频运动目标检测,并有效提升了基于基础背景差方法的运动目标检测效果,主要贡献包括:①针对前景检测问题,提出了四种中智属性,并提出了相应属性下的真(Truth)、不确定(Indeterminacy)、假(Falsity)量测计算方法;②综合利用一般单值中智集和多时段单值中智集相关度量测强化背景差图像序列中的运动目标区域,并基于此中智图像求解最优分割阈值。

1 相关中智集理论

1.1 单值中智集

假定X是一个全集,那么在X中的单值中智集A可以表示为:

A={[x,TA(x),IA(x),FA(x)]|x∈X}

(1)

式中:T(x),I(x)和F(x)分别表示对应元素的真、不确定和假分量量测函数,且TA(x),IA(x),FA(x)∈[0,1],0≤TA(x)+IA(x)+FA(x)≤3。

假定A={A1,A2,…,Am}是一个可供选择的集合,C={C1,C2,…,Cn}是一个条件属性集合,依照式(1),Ai可以被表示为:

Ai={〈Cj,TCj(Ai),ICj(Ai),FCj(Ai)〉|Cj∈C}i=1,2,…,m,j=1,2,…,n

(2)

式中:TCj(Ai),ICj(Ai)和FCj(Ai)是针对Ai,在条件属性Cj下的真、不确定和假分量量测函数,且TCj(Ai),ICj(Ai),FCj(Ai)∈[0,1],0≤TCj(Ai)+ICj(Ai)+FCj(Ai)≤3。A被称为多属性单值中智集。

1.2 相关度量测

文献[24]中提出了一种面向多属性单值中智集的相关度量测方法,Ai与Aj在属性Ck下的相关度(相似度)可以表示为:

(3)

若A*代表中智集范畴内理想情况下的选择,则任一选择Ai同A*的加权相关度可以表示为:

(4)

已有的单值中智集相关度量测主要针对某一时刻,为了解决这一问题,文献[21]针对多时段医疗诊断提出了分时的相似度量测方法。类似的,针对式(4),相应的多时段加权相关度量测可表示为:

(5)

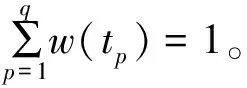
2 背景差基本模型

背景模型是指在视频图像获取过程中逐步建立的监控场景中长时间处于静止状态事物的图像表示。假定Bt-1是t-1时刻的背景图像,则t时刻的背景图像可通过如下方式获取:

Bt=(1-α)Bt-1+αIt

(6)

式中:It是指t时刻获取的图像,α是背景更新速率,α∈[0,1)。α越大,背景更新速度也越快,视频图像中的信息(包括运动区域)也更容易融入到背景图像中去,可能为背景图像带来较大干扰。当α为0时,表明背景图像不随时间变化。视频图像第一帧通常被作为B0。获取背景模型图像Bt后,运动目标区域可通过以下方法确定:

(7)

式中:It(x)和Bt(x)分别表示t时刻位于图像坐标x处的视频图像灰度值和背景图像灰度值,当二者差值超过阈值T时,认为图像中x坐标点属于运动目标区域,否则认为是静态背景区域。在本文中,St=|It-Bt|被称为背景差图像,该图像中对应像素点的值越大,则该像素点属于运动目标区域的可能性就越大。

3 中智运动区域检测

基本背景差模型提取前景区域的性能很大程度上依赖于阈值T的选取,在本文中,我们将背景差图像转换到中智集域,并将其称为中智背景差图像。我们通过多属性相关度量测生成中智背景差图像,强化运动目标区域,提升前景背景区分度,以此提升阈值T的选取准确性,最终提升运动区域检测性能。

3.1 中智背景差图像

假定U是一个全集,FP是集合U中的前景(运动目标区域)像素点集合,SNSt为t时刻的中智背景差图像。我们将SNSt中的某个像素点表示为:

PNSt(x)=(Tt(x),It(x),Ft(x))

(8)

式中:Tt(x),It(x),Ft(x)分别表示位于图像坐标x处的像素点属于FP、不确定是否属于FP、不属于FP的关系分量,Tt(x),It(x),Ft(x)∈[0,1],0≤Tt(x)+It(x)+Ft(x)≤3。若考虑到多条件属性,则SNSt中的某一像素点可以表示为:

(9)

式中:Cj表示某一条件属性。

经分析,在背景差图像St中,属于运动目标区域的像素点主要包含以下几方面特征:对应像素点的灰度值较高;对应像素点的较小邻域范围内灰度分布较均匀;对应像素点在连续数帧内灰度值较高;对应像素点在连续数帧内灰度值分布较均匀。基于此,我们提出了四种条件属性,并提出了相应条件属性下的真、不确定、假量测分量的计算方法。

对于灰度值强度条件属性Cg,与其对应的Tt(x),It(x),Ft(x)被定义如下:

(10)

SRt(x)={St(x+m,y+n)|m,n∈(-w/2,w/2)}

SRdt(x)=max{SRt(x)}-min{SRt(x)} >

(11)

(12)

均值滤波是图像增强中一种简单有效的图像平滑和降噪方法。因此我们将均值灰度强度作为第二个条件属性Cm,类似的,与之对应的Tt(x),It(x),Ft(x)被定义为:

(13)

(14)

(15)

考虑到稳定的运动目标区域具有一定的时域稳定性,即背景差图像中某一像素点的灰度值在一定时间序列上变化平缓甚至几乎不变。基于此种条件属性Cgv,与之对应的Tt(x),It(x),Ft(x)被定义为:

(16)

(17)

(18)

式中:Smet(x)表示在t时刻之前连续N帧背景差图像中位于坐标x处像素点所有时刻对应灰度值的中位数,即:

Smet(x)=median{St-N+1(x),St-N+2(x),…,St(x)}

(19)

SDvt(x)表示在t时刻之前连续N帧背景差图像中位于坐标x处像素点所有时刻对应灰度值所构成集合的标准方差,即:

SDv(x)=stddev{St-N+1(x),St-N+2(x),…,St(x)}

(20)

从式(16)～式(18)中可以看出,条件属性Cgv下的三类量测均已归一化处理。

最后,对于连续多帧的条件属性,我们将均值滤波也考虑进来,对于此类条件属性Cmv,与其对应的Tt(x),It(x),Ft(x)被定义为:

(21)

(22)

(23)

式中:Smmet(x)表示在t时刻之前连续N帧背景差图像中位于坐标x处像素点所有时刻对应邻域均值灰度值的中位数,即:

Smmet(x)=median{Smt-N+1(x),Smt-N+2(x),…,Smt(x)}

(24)

SmDvt(x)表示在t时刻之前连续N帧背景差图像中位于坐标x处像素点所有时刻对应邻域均值灰度值所构成集合的标准方差,即:

SmDv(x)=stddev{Smt-N+1(x),Smt-N+2(x),…,Smt(x)}

(25)

从以上分析可知,前两个条件属性主要针对静态帧内的运动区域像素点特征(空间域特征)提出,后两个条件属性主要针对连续动态帧内的运动区域像素点特征(时间域特征)提出。鉴于连续多帧分析可增强前景区域提取的鲁棒性,我们以t时刻之前连续N帧作为基本评价区间,联合面向单值中智集的多时段加权相关度量测和一般加权相关度量测,联合确定中智背景差图像各坐标处的灰度值。此处,我们假定四种条件属性下的理想选择均为A*=[1,0,0|,根据式(4)和式(5),中智背景差图像x坐标处的灰度值可表示为:

(26)

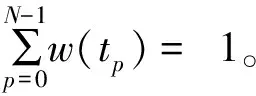
3.2 分割阈值自适应选取

在本文中,阈值分割主要针对中智背景差图像。在获取了t时刻中智背景差图像SNSt之后,最大类间方差(Otsu)方法被用来解决此问题,具体流程如下:

①选取某一灰度值作为初始阈值TNS;

②利用TNS将图像SNSt中所有的像素点分为两类,一类作为前景像素点集合,一类作为背景像素点集合,之后计算类间方差g=w0w1(u0-u1)2,其中u0、u1分别为两类像素点集合的灰度值均值,w0、w1分别为对应类别像素点数量占图像中总像素数量的比值;

③尝试其他灰度值作为分割阈值并计算相应的类间方差g,使得类间方差g最大的TNS被作为当前的最优分割阈值。

获取最优分割阈值TNS后,中智背景差图像SNSt中大于TNS的像素点被认为是运动区域像素点,否则为静止背景区域像素点。

图1 行人行走序列检测结果

4 实验结果

我们选取了几段有挑战性的视频用于测试,并将我们提出的中智前景提取算法与固定阈值前景提取算法(直接在传统背景差图像中采用固定阈值进行分割,此处简称FTFD)和Otsu自适应阈值提取方法(直接在传统背景差图像中采用Otsu方法进行阈值分割,此处简称OTFD)分别进行了比较,此外,我们也将算法结果与文献[25]提出的欧式距离前景提取算法(简称EDFD)进行了比较。

4.1 参数设置

对于FTFD、OTFD和我们提出的算法,式(6)中的背景更新速率α均被设置为0.01。式(11)和式(13)中的w被设置为5,式(19)、式(20)、式(24)～式(26)中的N均被设置为5。为了在一定程度上强化连续多帧的条件属性,式(26)中的wg、wm、wgv、wmv分别被设置为0.2、0.2、0.3、0.3。

4.2 运动目标检测结果

图1到图3给出了四种检测算法在三种不同场景下的检测结果。三个图中每一行对应某一帧的处理结果,从左至右各列分别为该帧时刻原图像、背景差图像,FTFD、OTFD、EDFD以及我们提出的算法的检测结果。图中白色区域代表被判定为运动目标的像素区域,黑色则代表背景区域。

图1为行人行走序列的检测结果,该序列的主要挑战因素是光照和影子。从图1第862帧和888帧中可以看出,在行人刚进入画面时,FTFD算法的检测结果存在一些离散噪点,其余三种算法表现较好。在第926帧,当行人的影子出现在画面中,且影子与路面颜色相差较大时,可以发现,OTFD和EDFD两种算法均受到了影响,由于FTFD自始至终都是采用一个固定分割阈值,它受到的影响最大。在第1 001帧,当行人逐步远离画面时,由于影子逐步落入草坪区域,而草坪在画面上的颜色与影子近似,相应背景差图像中对应像素点的灰度值也较小,因此OTFD获得了较好的检测效果,然而,由FTFD算法得到的结果仍包含了较多的影子区域。总体而言,我们的算法表现最好,即便在行人行进过程中仍会一定程度上受到影子问题的干扰,但多数情况能较好的将影子滤除。

图2为背景扰动序列的检测结果。该序列包含的主要挑战因素是背景扰动剧烈、运动目标小。从图2 可以看出,FTFD算法采用固定阈值,从运动目标进入画面到离开画面的整个过程中,所提取的运动区域均包含了大量的背景扰动噪声。由于背景扰动剧烈,运动目标区域以外的像素点灰度与背景差图像的差异较大,这是导致FTFD、EDFD算法被大量扰动背景干扰的主要原因。对于OTFD算法,它的表现存在极端现象。当目标刚进入画面时,由于目标区域很小,OTFD的前景提取效果很差,可见图2中第322帧的处理结果。对于第505帧,OTFD失败的原因主要是目标区域在背景差图像中与背景区域差别不够大。相反,我们提出的算法能够较好的克服背景扰动,其原因主要是我们将连续多帧的背景差图像像素点灰度时域分布做了特定限制,强化了在时域上表现较稳定且在当前帧邻域范围内分布较均匀的像素点。

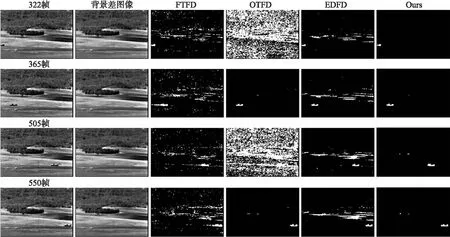
图2 背景扰动序列检测结果

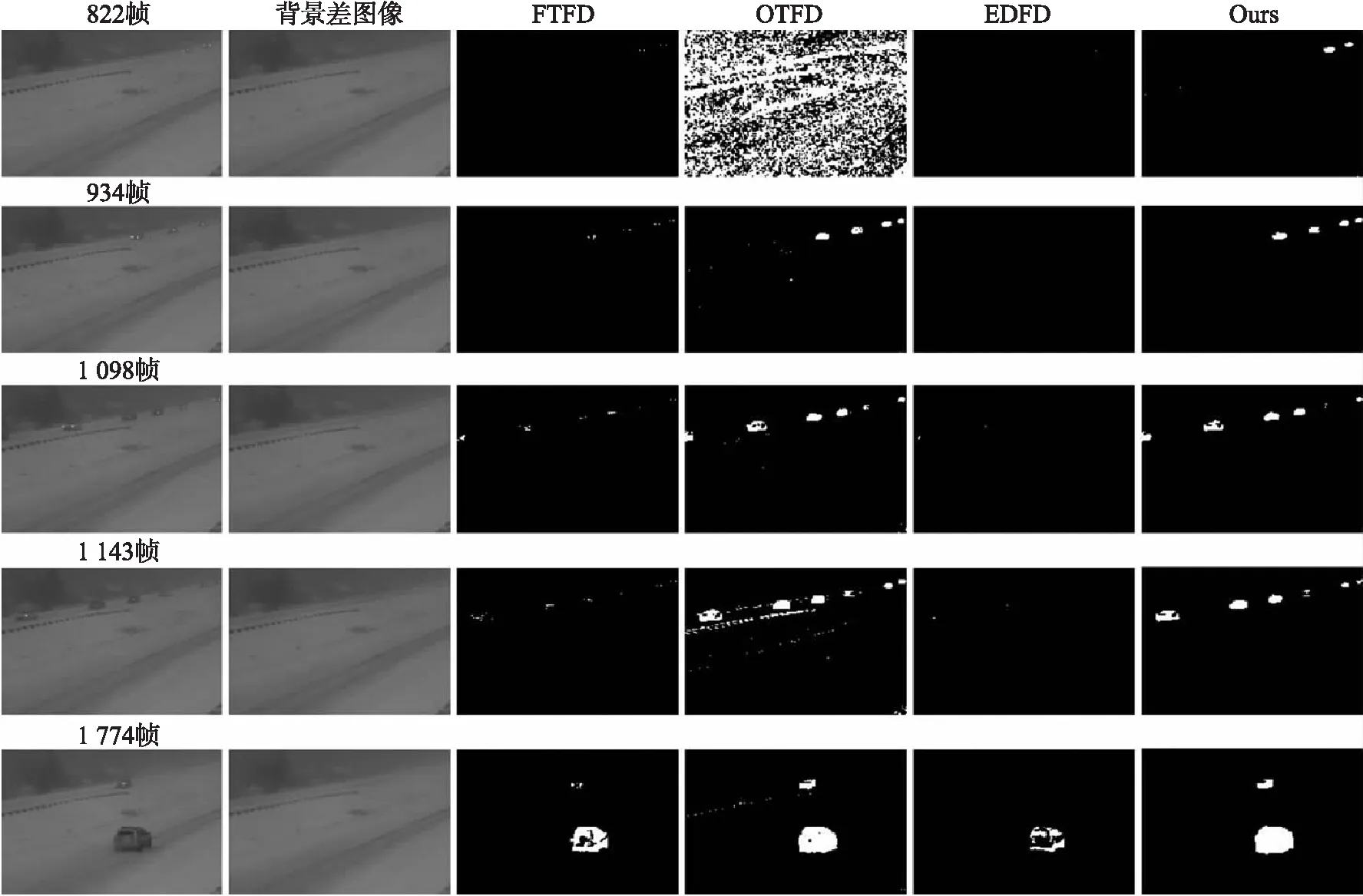
图3 恶劣天气序列检测结果

图3为恶劣天气序列的检测结果。该序列包含的主要挑战因素是对比度低、运动目标小、光照变化。从图3中可以发现,画面内主要包含两个单向车道,上方车道的车辆在画面中的成像区域较小,下方车道车辆成像区域较大。EDFD算法仅在第1 098帧和 1 143 帧检测到了上方车道上邻近摄像机的车辆,且仅有若干数量像素点,几乎无法判定是否存在运动目标。对于下方车道上成像较大的运动目标,EDFD成功捕获,然而相比其他三种算法,提取的运动区域存在较大空洞。在第822帧,FTFD的检测结果上仅较微弱的将车灯部分检测为运动区域,而我们的算法则较好的分离出了运动目标;对于OTFD,同样由于目标区域过小,其阈值选取失败。在第1 098帧,可以发现OTFD算法的表现要略优于我们的算法,我们的算法对由上至下第二个目标的检测效果较差。观察第 1 143 帧和1 774帧可以发现,当上方车道上车辆逐渐靠近摄像机时,车灯照射导致原本暗色区域变亮,OTFD将其误检测为运动目标区域;相较而言,我们的算法能较好的应对低对比度、小运动目标、光照变化等挑战。

4.3 理论模型与实验分析

综合以上分析,可以发现,我们的算法在应对光照变化、背景扰动、低对比度、小目标等挑战时的检测效果较好。对于运动目标检测问题,在由基本背景差模型获取的背景差图像中,运动目标对应的像素点具有灰度值较高的特点,且小邻域范围内像素灰度分布均匀的像素点属于运动目标像素点的可能性更高。基于此,算法在原背景差图像和经均值滤波后的背景差图像中,将像素点强度值作为真量测、将区域最大最小值之差作为不确定量测引入中智背景差图像。在时间域上,背景差图像中运动目标像素点应在短时间内保持一定强度的灰度值,且在此时间段内灰度值分布较均匀的像素点更有可能为运动目标像素点。鉴于此,算法以原背景差图像和经均值滤波后的背景差图像为基础,将像素点灰度时域中值作为真量测,将像素点时域灰度方差作为不确定量测引入。最终,结合中智加权相关度量测,将四种条件属性下的中智量测融合。光照变化、背景扰动、低对比度、小目标等条件下的动目标区域特点与我们所设定的运动目标像素点特征吻合,在着重考虑背景差图像中各像素点灰度值强度的同时,算法着重将时域稳定性和空域稳定性以多时段单值中智集和一般单值中智集相关度量测的方式融入到中智背景图像中,较好的强化了运动区域,提升了阈值选取的鲁棒性,最终表现出较好的运动目标检测性能。

5 结束语

本文在基本背景差模型的基础上,提出了一种基于多属性单值中智集相关度量测的视频运动目标检测方法。为了强化运动目标区域,本文将不确定性量测引入,提出了基于单值中智集的四种真、不确定和假量测。最终综合利用多周期单值中智集相关度量测和一般单值中智集相关度量测生成中智背景差图像,充分融合了像素点空间域和时间域上的约束信息。最后,基于中智背景差图像,借助最大类间方差方法获取最优分割阈值,完成前景区域提取。实验结果表明,在应对恶劣天气、背景扰动等挑战时,本文提出的算法体现出了较高的鲁棒性。

参考文献:

[1] Bouwmans T. Traditional and Recent Approaches in Background Modeling for Foreground Detection:An Overview[J]. Computer Science Review,2014,11-12(0):31-66.

[2] Thierry B,Fida El B,Bertrand V. Background Modeling Using Mixture of Gaussians for Foreground Detection—A Survey[J]. Recent Patents on Computer Science,2008,1(3):219-237.

[3] Stauffer C,Grimson W E L. Adaptive Background Mixture Models for Real-Time Tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Collins,Colorado;IEEE Press. 1999:22-29.

[4] Elgammal A,Duraiswami R,Harwood D,et al. Background and Foreground Modeling Using Nonparametric Kernel Density Estimation for Visual Surveillance[J]. Proceedings of The IEEE,2002,90(7):1151-1163.

[5] Gutchess D,Trajkovic M,Cohen-Solal E,et al. A Background Model Initialization Algorithm for Video Surveillance[C]//IEEE International Conference on Computer Vision.733-740.

[6] 张显亭,陈树越,陈颖鸣. 一种改进的复杂场景运动目标检测算法[J]. 传感技术学报,2009,22(8):1146-1149.

[7] 李喜来,李艾华,白向峰,等. 基于增量式特征基背景模型的运动目标检测[J]. 传感技术学报,2010,23(9):1293-1297.

[8] Bouwmans T. Background Subtraction for Visual Surveillance:A Fuzzy Approach[J]. Handbook on Soft Computing for Video Surveillance,2012:103-134.

[9] Maddalena L,Petrosino A. A Fuzzy Spatial Coherence-Based Approach to Background/Foreground Separation for Moving Object Detection[J]. Neural Computing and Applications,2010,19(2):179-186.

[10] Zhao Z,Bouwmans T,Zhang X,et al. A Fuzzy Background Modeling Approach for Motion Detection in Dynamic Backgrounds[J]. Multimedia and Signal Processing,2012:177-185.

[11] Smarandache F. Neutrosophy:Neutrosophic Probability,Set and Logic[M]. Rehoboth:American Research Press,1998:105.

[13] Anter A M,Hassanien A E,ElSoud M A A,et al. Neutrosophic Sets and FuzzyC-Means Clustering for Improving CT Liver Image Segmentation[J]. Advances in Intelligent Systems and Computing,2014,303:193-203.

[14] RehobothGuo Y,Xia R,engür A,et al. A Novel Image Segmentation Approach Based on Neutrosophicc-Means Clustering and Indeterminacy Filtering[J]. Neural Computing and Applications,2016:1-11.Rehoboh

[15] Hu K,Ye J,Fan E,et al. A Novel Object Tracking Algorithm by Fusing Color and Depth Information Based on Single Valued Neutrosophic Cross-Entropy[J]. Journal of Intelligent and Fuzzy Systems,2017,32(3):1775-1786.

[16] Guo Y,Sengur A. A novel 3D Skeleton Algorithm Based on Neutrosophic Cost Function[J]. Applied Soft Computing Journal,2015,36:210-217.

[18] 崔西希,吴成茂. 核空间中智模糊聚类及图像分割应用[J]. 中国图象图形学报,2016,21(10):1316-1327.

[19] Ye J. Single-Valued Neutrosophic Similarity Measures Based on Cotangent Function and Their Application in the Fault Diagnosis of Steam Turbine[J]. Soft Computing,2015,21(3):817-825.

[20] Ma Y X,Wang J Q,Wang J,et al. An Interval Neutrosophic Linguistic Multi-Criteria Group Decision-Making Method and its Application in Selecting Medical Treatment Options[J]. Neural Computing and Applications,2016:1-21.

[21] Ye J,Fu J. Multi-Period Medical Diagnosis Method Using a Single Valued Neutrosophic Similarity Measure Based on Tangent Function[J]. Computer Methods & Programs in Biomedicine,2016,123:142-149.

[22] Guo Y,Sengur A. NECM:Neutrosophic Evidentialc-Means Clustering Algorithm[J]. Neural Computing and Applications,2015,26(3):561-571.

[23] Guo Y,Sengur A. NCM:Neutrosophicc-Means Clustering Algorithm[J]. Pattern Recognition,2015,48(8):2710-2724.

[24] Ye J. Multicriteria Decision-Making Method Using the Correlation Coefficient under Single-Valued Neutrosophic Environment[J]. International Journal of General Systems,2013,42(4):386-394.

[25] Benezeth Y,Jodoin P M,Emile B,et al. Comparative Study of Background Subtraction Algorithms[J]. Journal of Electronic Imaging,2010,19(3):033003-033003-033012.