基于NMEA-BP的WSN数据流异常检测算法*

顾晓勇,李光辉,3*

(1.江南大学物联网工程学院,江苏 无锡 214122;2.江苏省无线传感网高技术研究重点实验室,南京 210003;3.物联网技术应用教育部工程技术研究中心,江苏 无锡 214122)

无线传感器网络是由大量微型、低成本的传感器节点组成。无线传感器节点通常被直接暴露在外界环境中进行环境信息的采集,如测量温度、湿度、降水量、光照强度等。正常情况下测量的数据在一定范围内缓慢波动,但当无线传感网络遭受外部事件(如火灾、降雨、空气污染等)的影响,或节点自身的软硬件故障(如电池能量不足、节点故障、软件缺陷等)时,节点观测值显著偏离于正常模型,通常被称为离群值[1]。因此,针对传感器数据流进行离群检测,对于保证传感器网络的数据质量具有重要意义。

关于无线传感网络异常数据检测方法,国内外学术界已有很多研究成果[2-5]。潘轶彪等[6]提出了一种采用历史数据集建立模型,估计当前读数,并按照真实值与估计值间的差异检测异常的方法。Yao等[7]提出了一种高效的在线异常检测算法,该算法利用时间序列的分段线性模型,分别构造参考时间序列和新的时间序列模型,通过求它们之间的相似度量值来捕捉时间序列中的差异,寻找该序列中的异常,该方法可以查找长时间的异常。Zhang等[8]提出了基于SVM模型的自适应离群检测算法,首先利用数据流的时间相关性在本地节点建立模型,判断数据是否为局部离群点,再接收来自邻居节点的相关系数,利用空间相关性整合得全局检测模型,可以找出全局离群点。近年来,许多学者用BPNN检测异常数据,但BPNN存在局部最优解,训练时间长,效率低等问题。屈洪春等[9]提出了利用遗传算法优化BP神经网络的算法,并应用于异常检测,相比BPNN该算法改善了优化的精度和异常检测率。但是遗传算法的缺点也日益明显,随机搜索会导致过早收敛,思维进化算法[10]就可以很好的解决这个问题,但是它也存在局部搜索随机性等问题。

针对上述问题,本文提出了一种基于小生境的思维进化算法,用来优化BPNN参数,由此获得了一种新的传感器网络异常数据检测算法。

1 算法原理

BP神经网络[11]是一种按误差逆向传播训练的多层前馈网络。结构如图1所示,X1,X2,…,Xn是BP神经网络的输入值,Y1,Y2,…,Ym是BP神经网络的预测值。网络输入层为n,隐含层为l,输出层为m。

图1 BP神经网络结构

思维进化算法[12]的基本思想是把群体划分为若干个子群体,个体在子群体内通过向优胜者学习,为成为优胜子群体而展开全局竞争。思维进化算法过程中添加了记忆与定向学习机制,改善了搜索效率。

小生境技术的基本思想是将每一代个体划分为若干类,每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群体,再在不同群体之间进行杂交、变异产生新一代群体,并且采用预选择机制、排挤机制或分享机制以及聚类机制等完成选择任务。在遗传算法中,小生境技术主要采用排挤法和共享法,这两种方法均需较多的个体参与竞争和共享资源,造成了时间的浪费。本文用文献[13]中的RCS(Restricted Competition Selection)方法生成小生境,该方法只需几个简单的个体就可以完成。通过控制子群体之间的排斥和竞争,使各个子群体在进化过程中动态形成各自独立的搜索空间,从而保持群体的多样性。该算法如下所示,NMEA算法中有m个子群体,子群体的优胜者为Umbest。

设两子群体优胜者间的距离为dij,s为个体编码长度:

(1)

小生境算法如表1所示。

表1 小生境算法

2 基于NMEA的BPNN异常检测算法

本文考虑将NMEA与BPNN结合起来,寻求新的传感器网络异常数据检测算法。将BPNN与NMEA相结合,以避免网络陷入局部极小值。在思维进化算法中,采用实数编码法,根据BPNN结构将解空间映射到编码空间,每个编码空间对应一个个体。定义NMEA中的个体为BPNN中的一组待优化的权阈值,寻找最优个体得到最优的网络结构,建立检测模型并进行异常检测。神经网络的训练终止条件是样本与网络实际输出值的均方误差达到最小(对应NMEA中的得分函数最大),公式为:

(2)

(3)

NMEA优化的权阈值总数为s=nl+ml+l+m。用NMEA优化的权阈值作为BPNN的初始值,然后构建模型进行训练。本文提出的异常检测算法包括基于NMEA的BPNN参数优化和传感器数据流异常检测两个阶段。

2.1 基于NMEA的BPNN参数优化

传统的MEA对局部的搜索具有随机性,受文献[13]的启发,本文提出了一种新的思维进化算法。具体步骤如下:

Step 1 随机生成N个个体形成初始群体,按照式(2)、式(3)计算各个个体的得分。

Step 2 按照个体得分从大到小进行排序,选取前q个个体为优胜者,分别以优胜者为中心形成子群体。

Step 3 生成小生境。对q个子群体的优胜者分别按照式(1)计算优胜者间的得分,得分低的个体将被丢弃,生成新的个体,直到产生各自的搜索空间。

Step 4 分别以优胜者为中心生成新的子群体。

Step 5 在小生境中执行趋同操作,查找局部最优解。

Step 6 比较成熟群体的得分,分数最少的子群体被丢弃,生成新的个体。

Step 7 将生成的新的个体与整个群体的优胜者按照式(1)进行相比,直到新生成的个体在不同的小生境中。

Step 8 当最优胜者的得分不再变化时则停止迭代,得到最优解;否则转Step4。

2.2 基于最优BPNN的传感器网络异常数据检测

2.2.1 滑动窗口模型

本文使用滑动窗口模型处理传感器数据流,该模型是用来查看传感器节点最近一个采样时间段的数据,即对传感器数据流选取一个固定长度的窗口。

如图2所示,滑动窗口大小为n。若在t时刻窗口中存储数据为{Xt-n+1,…,Xt-1,Xt},则在t+1时刻

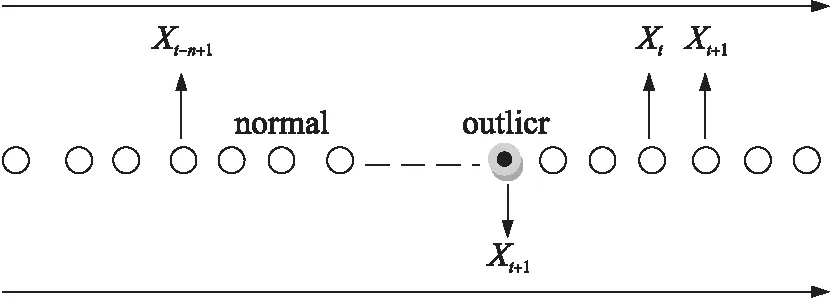
图2 滑动窗口模型

2.2.2 异常检测过程

首先利用历史数据训练神经网络,获得下一时刻的采样预测值。然后选取训练数据的后v个样本数计算神经网络的模型残差,并确定置信区间范围。当下一时刻的数据在区间范围内,则该数据为正常值;反之,则为异常值。公式如下:

(4)

式中:S为神经网络模型残差,v代表选取的样本数,Ei(i=1,2,…,v)为选取的样本值,F代表所选取样本的平均值。

置信区间的上、下界分别用如下公式给出:

(5)

(6)

Step 1 输入数据到滑动窗口{Xt-n+1,…,Xt-1,Xt}中。

Step 2 读取下一时刻的数据Xt+1,利用训练好的模型获得该时刻的预测值t+1,按照式(4)～式(6)计算置信区间范围。

Step 4 判断数据读取情况。若下一时刻数据能够读取,转Step 2,否则结束。

综上所述,本文提出的NMEA-BP异常检测算法如表2所示。

表2 NMEA-BP异常检测算法

3 实验结果及分析

为了评估NMEA-BP异常检测算法的性能,本文使用因特尔伯克利实验室的无线传感网络数据集(IBRL)以及文献[15]提供的带标记传感网络数据集(LWSNDR)完成了仿真实验。实验是在Intel(R)Core(TM)i5-2450MCPU,主频2.5GHz,内存8G,操作系统Window8环境下进行的,编程语言采用MATLAB2014a。分别实现了BP、NMEA-BP、SVM以及ELM算法,并进行了实验结果的比较。

3.1 数据集

IBRL数据集来自于部署在IntelBerkeley实验室中的无线传感器网络,该网络有54个MICA2传感器节点,采样周期为30s,运行周期为2004年2月28日到2004年4月5日,每个节点的数据包括温度、湿度、光照及电压4个属性。本文分别选取7号传感器节点2004年2月28日1点到16点的温度、湿度采样数据,选取9号传感器节点2004年2月28日8点到2004年2月29日22点的温度、湿度采样数据,选取29号传感器节点2004年3月5日17点到2004年3月8日4点的温度、湿度采样数据,选取7号传感器节点2004年3月5日17点到2004年3月8日5点的温度、湿度采样数据作为本实验数据集。LWSNDR数据集采集的是室内和室外的温度、湿度数据,选取两组室外的数据LWSNDR-1和LWSNDR-2。由于样本数据集中异常值较少,实验过程中我们人工随机地添加异常值。实验数据集如表3所示。

表3 实验所用数据集

3.2 性能评价指标

对于二分类问题,可将样本根据其真实类别和决策模型检测类别的组合划分成真正例TP(True Positive)、假正例FP(False Positive)、真反例TN(True Negative)、假反例FN(False Negative)4种情形。

为了评价算法的性能,本文使用检测率TPR(True Positive Rate)和误报率FPR(False Positive Rate)两个指标。公式如下:

(7)

(8)

3.3 参数设定

BPNN的训练参数如表4所示。Show为训练过程中的显示步数;Lr为神经网络的学习速率;Epochs为神经网络允许的最大训练步数;Goal为神经网络的目标精度。

表4 BP神经网络的训练参数

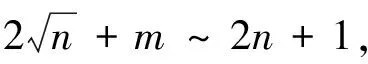
3.4 BP神经网络参数优化的对比实验

为验证本文提出的小生境思维进化优化算法的效率,在IBRL_7的训练数据中选取4组不同规模的数据,为500、1 000、1 500、2 000个数据,同时在LWSNDR-2训练数据集上选取4组不同规模的数据,为300、600、900、1 200个数据。分别使用BP算法和NMEA-BP算法在不同规模数据集上做训练,并用训练时间作为衡量指标,实验结果如图3所示,横坐标代表选取的数据样本序号,纵坐标代表训练时间。由图3(a)可知,在IBRL数据集上,BP算法平均训练时间为32 s,NMEA-BP算法在训练时间方面优势较明显,平均训练时间为24 s,相对BP算法训练时间减少25%;由图3(b)可知,在LWSNDR数据集上,BP算法平均训练时间为17 s,NMEA-BP算法平均训练时间为11 s,相对BP算法训练时间减少33%。这是由于NMEA算法使用更短的速度达到了误差要求缩短了训练时间。

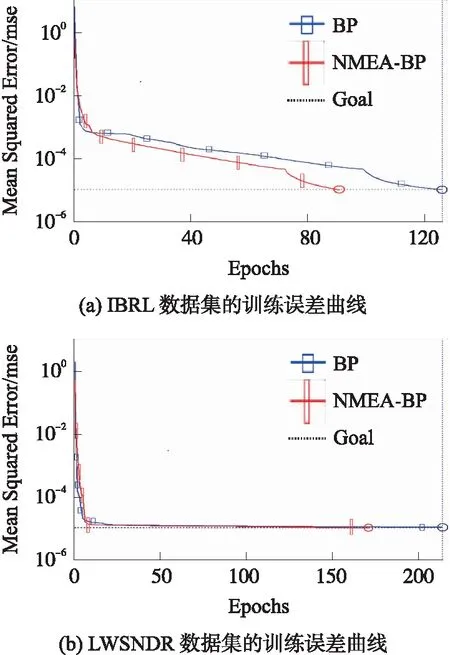
图4 BP算法和NMEA-BP算法的误差平方和曲线

图3 BP算法和NMEA-BP算法在不同规模数据集上的训练时间

选取数据集IBRL_7和LWSNDR-2的神经网络误差平方和曲线,横坐标代表训练步数,纵坐标代表均方误差。由图4(a)可得,在同样目标误差下,NMEA-BP算法达到训练误差时需要172步,而BP算法需要214步达到训练误差;由图4(b)可得,在同样目标误差下,NMEA-BP算法达到训练误差时需要91步,而BP算法需要126步达到训练误差。证明经NMEA算法优化后的BPNN的权阈值得到了全局寻优,有更好的收敛效果。

3.5 异常检测算法的对比实验

为了评估NMEA-BP算法性能,分别在上述6个数据集上进行对比实验,结果如表5和表6所示。从表5可以看出,在不同的数据集下,NMEA-BP算法TPR比BP、ELM、SVM算法平均提高了0.8%、1.92%、3.2%;NMEA-BP算法FPR比BP、ELM、SVM算法平均降低了1.65%、2.13%、2.15%。从表5还可以发现,SVM算法在数据集Ⅱ,Ⅲ,Ⅳ上TPR和FPR较好,但SVM算法在数据集Ⅰ上FPR偏高是由于训练样本较少,数据分布不均匀导致的,与NMEA-BP算法对比,FPR相对偏高,TPR稍低。ELM算法在4个数据集上都表现出了较高的TPR,而在数据Ⅰ中FPR相对偏高是由于ELM隐层神经元数目是随机的,建立的检测模型不够稳定,就决定了TPR和FPR的高低。BP算法虽然对于训练集的数据能很好地拟合,但由于数据集Ⅰ的测试数据和异常数据的差距较小,算法求得的置信区间范围较小,导致该数据集的误报率偏高。NMEA-BP算法在数据集Ⅰ上的误报率比BP算法降低了5.8%,这是由于优化后的模型预测更精确,置信区间的范围相对准确。在其他3个数据集上大部分异常样本与正常样本区分度较高,可以很容易检测出来。从表6可以看出,在不同的数据集下,NMEA-BP算法和BP算法均表现出较好的检测结果,而SVM算法和ELM算法的检测率相对偏低,这是数据分布不均匀导致的。因此,NMEA-BP算法具有更好的检测性能。

表5 关于IBRL数据集的算法性能对比

表6 关于LWSNDR数据集的算法性能对比

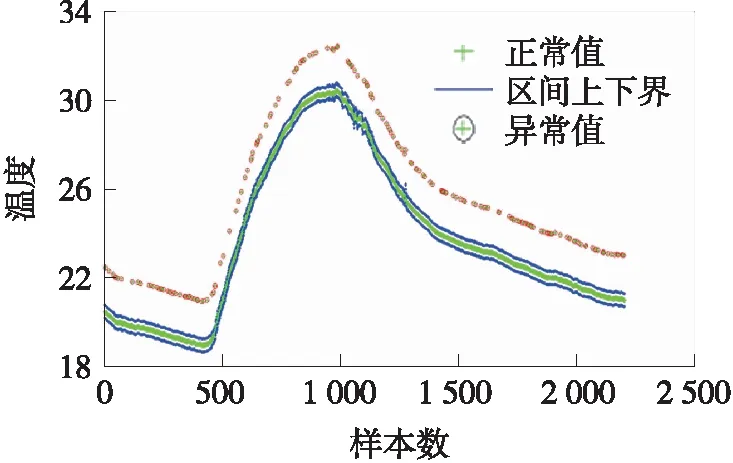
图5 NMEA-BP算法的异常检测结果

为了更直观地阐明NMEA-BP算法的异常检测过程,现以数据集Ⅲ为例说明。图5给出了NMEA-BP的异常检测结果。其中,横坐标为样本数,纵坐标为温度,根据置信区间判断异常,两条线段代表区间的上下界,用圆圈圈出的则为异常值。选取第1 000个样本的数据,其值为30.11,而NMEA-BP算法的预测值为30.21,通过区间公式计算置信区间,为[29.91,30.51],故算法判定该样本为正常值;若样本值不在置信区间范围内,则算法判定该样本为异常值。

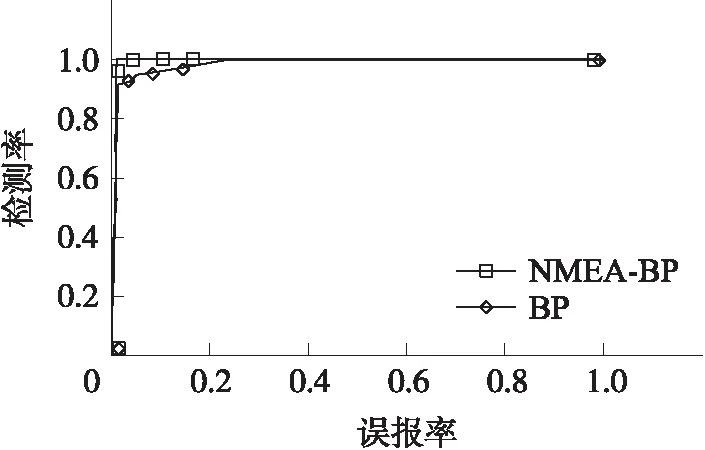
图6 BP算法和NMEA-BP算法的ROC曲线

在对不同算法进行比较时,较为合理的判断依据是比较ROC(Receiver Operating Characteristic)曲线下的面积[16],即AUC(Area Under ROC Curve),该方法简单,直观,通过图示就可以观察分析方法的准确性。图6给出了NMEA-BP和BP两种算法的ROC曲线。其中,横坐标代表FPR,纵坐标代表TPR。

由图6可以发现BP算法ROC曲线被NMEA-BP算法ROC曲线完全包住,ROC曲线越靠近左上角表明其TPR更好,因此,NMEA-BP算法的ROC曲线有更大的AUC。NMEA-BP算法在TPR接近100%时FPR仅为1.5%,而BP算法此时的TPR为92%左右,故NMEA-BP算法具有更好的检测性能。

4 结论

本文提出了一种基于NMEA-BP的传感器网络数据流异常检测算法。该算法将小生境技术与思维进化相结合,对BPNN的权阈值进行寻优,克服了传统BPNN收敛速度慢和易陷入局部极小的缺陷等问题,加快了BPNN学习速率。NMEA-BP算法在异常检测率较高的同时减少了训练时间。实验结果表明,与其他同类算法相比,NMEA-BP算法对传感器数据流的异常检测有更高的检测率和更低的误报率。本文算法是利用时间相关性检测的,今后的研究将考虑利用节点间的空间相关性,以便进一步提高检测率,降低误报率。

参考文献:

[1] 李建中,高宏. 无线传感器网络的研究进展[J]. 计算机研究与发展,2008,45(1):1-15.

[2] 李娟娟,孟国营,谢广明,等. 基于小波包与SOM神经网络的传感器故障诊断[J]. 传感技术学报,2017,30(7):1035-1039.

[3] Mainwaring A,Polastre J,Szewczyk R,et al. Wireless Sensor Networks for Habitat Monitoring[C]//Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications. IEEE,2002:88-97.

[4] 孙利民,李建中,陈渝,等. 无线传感器网络[M]. 北京:清华大学出版社,2005:407-417.

[5] McDonald D,Sanchez S,Madria S,et a1. A Survey of Methods for Finding Outliers in Wireless Sensor Networks[J]. Journal of Network and Systems Management,2015,23(1):1-20.

[6] 潘轶彪,袁景淇,朱凯,等. 基于多层感知器的异常数据实时检测方法[J]. 上海交通大学学报,2011,45(8):1226-1229.

[7] Yao Y,Sharma A,Golubchik L,et a1. Online Anomaly Detection for Sensor Systems:A simple and efficient approach[J]. Performance Evaluation,2010,67(11):1059-1075.

[8] Zhang Y,Meratnia N,Havinga P J M. Distributed Online Outlier Detection in Wireless Sensor Networks Using Ellipsoidal Support Vector Machine[J]. Ad Hoc Networks,2013,11(3):1062-1074.

[9] 屈洪春,王帅. 一种基于进化神经网络的混合入侵检测模型[J]. 计算机科学,2016,43(S1):335-338.

[10] Gao J L. Modeling of Photovoltaic Cell Based on BP Neural Networks Improved by MEA[J]. Applied Mechanics and Materials,2012,217-219:809-814.

[11] 孙艳梅,苗凤娟,陶佰睿. 基于PSO的BP神经网络在压力传感器温度补偿中的应用[J]. 传感技术学报,2014,27(3):342-346.

[12] Sun C Y. Mind-Evolution-Based Machine Learning:Framework and the Implementation of Optimization[C]//Proceeding of International Conference on Intelligent Engineering Systems. IEEE,1998:355-359.

[13] Lee CG,Cho D H,Jung H K. Niche Genetic Algorithm with Restricted Competition Selection for Multimodal Function Optimization[J]. IEEE Transaction on Magnetics,1999,35(1):1722-1725.

[14] Hill D J,Minsker B S. Anomaly Detection in Streaming Environmental Sensor Data:A Data-Driven Modeling Approach[J]. Environmental Modeling and Software,2010,25(9):1014-1022.

[15] Shan S,Alzahrani M,Rajasegarar S,et al. Labeled Data Collection for Anomaly Detection in Wireless Sensor Networks[C]//Proceeding of International Conference on Intelligent Sensors. IEEE,2010:269-274.

[16] 周志华. 机器学习[M]. 北京:清华大学出版社,2016:33-35.