足式机器人腿部倾角传感器信号处理研究

2018-06-12王中立李丽宏

传感技术学报 2018年5期

王中立,李丽宏

(太原理工大学信息工程学院,太原 030024)

随着科技的进步以及经济的发展,移动机器人需要不仅能在结构化环境下定点作业,还能在非结构化环境下非定点作业,比如,深海探测、地质灾害救援和军事目标追踪等非结构化环境,从而代替人类完成危险任务以及到达人类不能到达的区域。普通的轮式移动机器人很难适应非结构化环境,由于足式机器人仅需满足一定的离散落足点即可步行移动,因此足式机器人能更好地适应非结构化环境。

腿部是足式机器人准确行走以及适应非结构化环境的关键,由于足式机器人的姿态受到腿部状态影响,因此腿部是决定机器人姿态的关键因素[1]。为了更好地获取足端位置,本文利用高精度双轴传感器SCA1000测量腿部各个关节旋转角度,实现对足式机器人足端精确定位。然而足式机器人工作环境多是非结构的户外环境,受各种因素影响,倾角传感器测量误差大,再加上足式机器人长时间行走后,测量误差累计,导致足式机器人腿部倾角传感器测量不准确,难以根据倾角传感器信号利用运动学模型分析腿部状态。所以,如何处理腿部倾角传感器信号是现如今足式机器人研究领域的热点和难点。

现如今已有很多学者对提高倾角传感器测量精度方面进行了大量的研究,例如:朱月青等研究了温度对倾角传感器的影响,通过利用BP神经网络方法融合倾角传感器输出信号,将传感器的测量误差控制在2%以内[2];邵晓敏等研究了倾角传感器输入和输出的关系,利用最小二乘法对传感器进行信号处理,将倾角传感器输出信号的误差控制在1.7%以内[3]等等。尽管以上研究在某种程度上提高了倾角传感器的测量精度,但信号处理精度仍然偏低。为了进一步提高测量精度,本文先利用卡尔曼滤波算法对倾角传感器信号进行滤波预处理,再采用径向基函数RBF(Radial Basis Function)神经网络模型对滤波预处理的信号进行温度补偿,而对于RBF神经网络隐含层基函数中心值的选取,则利用具有并行寻优特征和自适应挥发系数的蚁群聚类算法,更改信息量,使算法能够搜索全局最优解,提高了RBF网络的训练速度以及鲁棒性。

1 足式机器人腿部系统概述

足式机器人腿部主要包括大腿、小腿和支撑脚盘,系统结构如图1所示。倾角传感器安装位置如图所示,其主要测量大腿和小腿的旋转角度值,通过得到的角度值再根据腿部运动学方程可以得到足端状态,也可以联合多条腿的角度值来估计机器人位姿。足端估计原理如图2所示。

图1 足式机器人腿部结构

图2 定位足端原理框图

2 腿部倾角传感器工作原理

SCA1000是采用三维MEMS(Micro Electro Mechanical System)技术开发的高精度双轴倾角测量传感器,能够测量相对于水平面的倾斜角度以及俯仰角度,同时也能测量所处环境的温度。内部主要组成包括:硅敏感电容传感器、存储器、温度传感器、A/D转换器、感应元件、信号调理电路、滤波电路和SPI通信接口等[4]。该传感器可以分别通过X通道、Y通道测量倾斜加速度、俯仰加速度,测得的信号既可以是数字信号也可以是模拟信号,最终通过SPI通信接口传输到控制器,同时也可以输出温度信号。

倾角传感器内部具有对加速度敏感的质量块,悬臂弹簧把质量块固定在敏感器上,并且一对电极板置于质量块的上下方,等似于一个电容,该电容是一种极距变化电容。当倾角传感器发生倾斜时,由于重力作用,倾角传感器中质量块发生偏移,导致两片电极板与质量块之间的距离发生相对变化,因此,电容发生变化,最终导致电压变化。电压值可以反映加速度值,再通过相应的计算得到角度值。

倾角传感器的角度输出可以利用模拟量电压值或者数字量进行转换。

电压到角度转换公式:

(1)

式中:Offset是在0°输出的电压值;Sen是灵敏度;Vout是芯片输出的模拟量。

数字量到角度转换公式:

(2)

式中:Dout是X或Y通道的数字输出量;Dout@0°是数值抵消量(一般倾角为0°时,输出1 024数字量);Sen是芯片灵敏度。

SCA1000内部温度传感器测量温度值为8 bit数据,既可以作为内在补偿,也可以作为外部补偿,转换公式:

(3)

式中:Counts是读取的温度量;T是转换后的温度量,单位是 ℃。

3 倾角信号滤波预处理

3.1 卡尔曼滤波原理

假设一个研究对象是随机线性离散系统,那么其卡尔曼滤波状态方程表示为:

X(k)=S(k)X(k-1)+B(k)U(k)+W(k)

(4)

式中:X(k)是研究对象的状态向量;S(k)是状态转移矩阵;B(k)是输入控制矩阵;U(k)是控制向量;W(k)可以看作均值为0,协方差为σk的正态分布的过程噪声。

观测方程可表示为:

Z(k)=H(k)X(k)+V(k)

(5)

式中:Z(k)是研究对象的观测向量;H(k)是观测矩阵;V(k)为观测噪声矩阵。

卡尔曼滤波器的递推过程主要分为2部分:预测和更新。在预测部分时,卡尔曼滤波器利用上一状态的估计值来估计当前状态的值;在更新部分时,卡尔曼滤波器会利用当前状态的观测值来补偿预测阶段获得的预测值,使新获得的估计值更为精确[5-7]。

假设控制信号向量U(k)=0,则状态预测方程为:

X(k|k-1)=S(k)X(k-1|k-1)

(6)

预测误差协方差估计为:

(7)

式中:Q(k)是系统噪声协方差阵。

更新方程为:

K(k)=P(k|k-1)HT(k)[H(k)P(k|k-1)HT(k)+R(k)]-1

(8)

式中:R(k)为测量噪声协方差阵。

状态估计为:

X(k|k)=X(k|k-1)+K(k)[Z(k)-H(k)X(k|k-1)]

(9)

最优解在更新k状态下所对应的误差协方差为:

P(k|k)=[1-K(k)H(k)]P(k|k-1)

(10)

由上式可知,除了给定滤波初值X(0|0)和P(0|0)以及k时刻的观测值Z(k)之外,还需要根据实际应用调整Q和R的取值,Q和R可以通过对象模型和采集离线数据获得,最后通过递推计算得出k时刻的状态估计值X(k|k)和误差协方差P(k|k)。

图3 卡尔曼滤波前后倾角信号误差对比图

3.2 卡尔曼滤波在信号处理中的应用

本文针对SCA1000高精度双轴倾角传感器输出的倾角信号进行卡尔曼滤波,在滤波时,先将SCA1000倾角传感器固定在三轴精密转台上,连续采集150组输出信号和倾角传感器输出信号,并计算倾角传感器输出信号的平均值和方差,分别作为滤波初值X(0|0)和P(0|0)。Q是滤波参数且反映的是对象模型噪声方差,当模型确定时,可以把此参数定位极小值;R是测量方差,可以通过采集数据求得,本文为了得到良好的滤波效果,根据经验确定Q的取值为1×10-6,R的取值为0.001 5。

本文利用MatLab 2014b仿真软件进行卡尔曼滤波仿真分析,利用软件中设计的滤波器处理采集数据,得到倾角误差波形图如图3所示。

从图3可知,经过卡尔曼滤波后倾角信号中的随机噪声明显减少,提高了倾角信号的稳定性和精确度。为了进一步提高倾角传感器测量精度,再把滤波信号作为建立的RBF神经网络样本数据。

4 RBF神经网络原理及模型建立

4.1 RBF神经网络原理

RBF神经网络是包含输入层、隐含层和输出层的三层前馈单隐层网络,利用非线性基函数的线性组合来实现映射关系[8],其结构如图4所示。

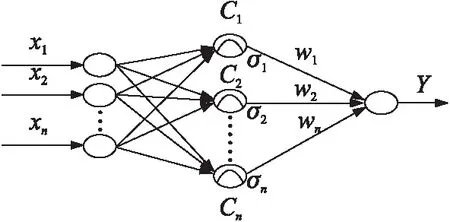
图4 RBF神经网络结构

输入层仅起到信号传输的作用,输入层和隐含层之间的连接权值为1;隐含层神经元的激活函数为径向基函数,它是中心点径向对称且衰减的非负线性函数,此函数局部响应函数采用非线性优化策略;输出层是对输入模式做出的响应,对线性权值进行调整,采用线性化策略,学习速度较快[9-11]。本文中RBF神经网络隐含层节点的径向基函数选用高斯函数:

(11)

式中:σ为基函数的扩展常数或宽度。

设输入样本为X=(x1,x2,…,xn),单输出为y,隐含层节点输出为D=(d0,d2,…,dm),隐含层节点到输出节点的连接权重为W=(w1,w2,…,wm),当高斯函数作为隐含层节点的激励函数时,RBF神经网络的单输出Y表示为:

(12)

式中:m是隐含层节点数;wi是第i个隐含层节点与输出层节点连接权值;‖·‖是欧几里得范数;Ci是第i个隐含层节点中心参数。

4.2 模型建立

4.2.1 基于蚁群算法的RBF神经网络训练

在处理大样本数据时,一般聚类算法,如K均值聚类算法,存在聚类慢、易陷入局部最优问题中,难以获得最优结果,因此,本文采用蚁群算法,蚁群算法是人们在观察蚁群觅食行为时受到启发而提出的。蚂蚁在觅食过程中,会在经过的地方留下一些物质,这些物质就是信息素[12]。而路径上信息素的多少,会决定同一群蚂蚁行进的方向,它们通过比较路径上信息素浓度大小,选择浓度大的方向前进,同时,也会在该路径上留下自己的信息素。相同时间内,路径越短,则被越多的蚂蚁访问,所以,后续的蚂蚁选择该路径的可能性越大,因此,该路径就是到达目标食物的最佳路径[13-14]。利用蚁群算法进行聚类分析时,聚类中心为目标食物源,把数据看作具有不同属性的蚂蚁,聚类过程就等同于蚂蚁寻找食物。其聚类详细过程[15]如下:

①基本参数初始化:样本数量为N,样本属性为m,聚类半径为r,误差允许值为ξ0,参考概率为p。

②求出任意两样本间的欧式距离Lij:

Lij=‖xi-xj‖,i,j=1,2,…,N

(13)

③对路径上的信息素τij进行初始化可以依据如下公式:

(14)

④xi和xj之间的概率为:

(15)

如果值pij(t)不少于预先设定值p0,则把xi归属于xj类,否则为不同的两个类。

若误差ξ<ξ0,则停止,否则继续。

⑥得到新的聚类中心与各样本间的距离Lij,改变信息素的挥发系数:

(16)

式中:ρ为挥发系数,ρ的最小值为ρmin;t为时间,则t、t-1时刻的挥发系数分别为ρ(t)、ρ(t-1)。调整信息素:

式中,S为信息强度,是一个常数。

⑦重复进行步骤④～步骤⑥直到满足预设误差为止,最后得到聚类中心以及聚类数。

4.2.2RBF神经网络设计及样本数据处理

通过蚁群算法得到的聚类中心作为隐含层单元中心值,然后通过最小二乘法来直接求出隐含层到输出层的连接权值。

利用RBF神经网络处理倾角传感器输出信号时,应确定输入层以及输出层节点个数。由于倾角传感器测量时易受温度影响,因此,把倾角传感器输出的温度信号和经过滤波处理的倾角信号作为RBF网络输入量,确定输入层节点个数为2个。由于需得到精确的倾角传感器输出信号,所以把倾角信号作为输出,即输出层为单输出。

为了控制RBF神经网络规模以及确保其训练的准确性和不出现饱和状况,对采集的温度数据和滤波后的倾角信号进行归一化处理,使样本数据落在区间[0,1]之内,归一化公式如下:

Xi=(di-dimax)/(dimin-dimax)

(17)

式中:Xi是样本数据的归一化;di是样本数据的原始数据;dimin,dimax分别是数据的最小值、最大值。

5 实验验证及分析

把SCA1000倾角传感器放在三轴精密转台上,通过改变外界温度和转台角度,采集包括三轴精密转台的倾角信号以及倾角传感器的温度信号、倾角信号,从采集数据中随机选取50组数据。首先,对采集的倾角传感器的倾角信号进行卡尔曼滤波处理,然后再随机选取30组温度数据和滤波后的倾角传感器输出信号经过归一化后,用于RBF神经网络训练,其余20组数据用作测试样本。

利用MATLAB 2014b中的神经网络工具箱来训练RBF神经网络,根据经验值以及补偿精度要求,设置基于蚁群算法的RBF神经网络各参数如下:r=0.4,ξ0=0.003,ρmin=0.3,S=25,p0=0.5。建立一个隐含层单元中心点个数为6个,目标误差为1×10-6的RBF神经网络。再利用其余20组数据测试训练好的RBF神经网络。经过25次训练达到目标训练精度,神经网络误差收敛曲线如图5所示。

图5 RBF神经网络误差收敛曲线

从50组数据中随机选取10组数据,然后对卡尔曼滤波后的数据与先通过卡尔曼滤波再进行基于蚁群聚类算法的RBF神经网络温度补偿的数据误差相比较,得到如表1所示的信号误差比较结果。

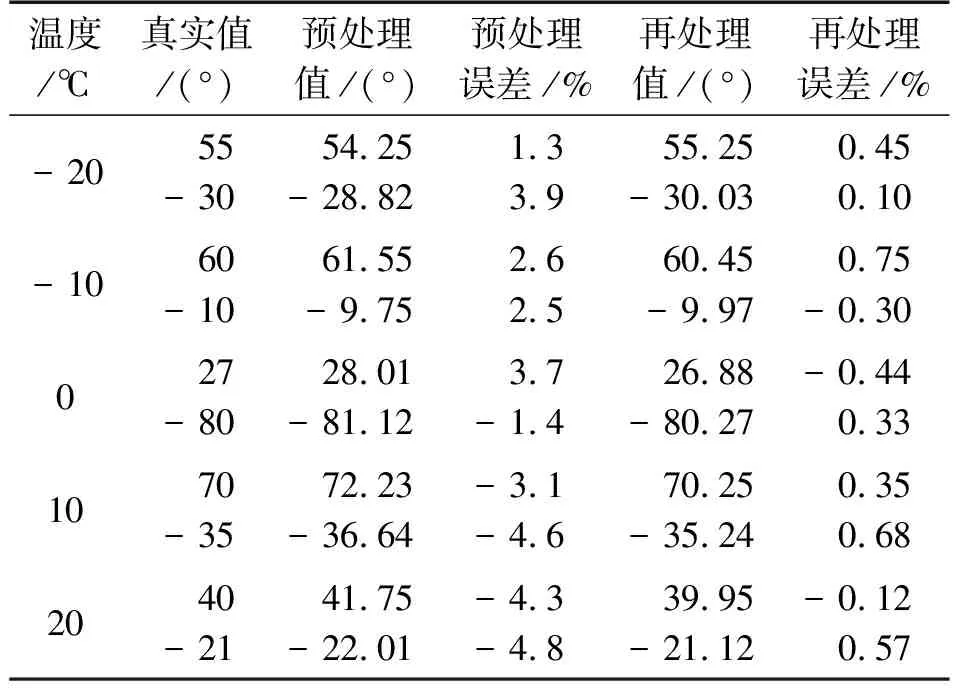
表1 实验数据误差比较

由表1得出,经过卡尔曼滤波预处理后的倾角传感器测量误差较大,不能达到良好的信号处理效果,为了达到较高的测量精度,再把温度信号和预处理的倾角信号作为基于蚁群聚类算法的RBF神经网络的输入信号,对倾角信号进行温度补偿,能把倾角测量误差控制在0.75%以内。

6 结论

足式机器人腿部倾角传感器易受外界环境的影响,特别是外界温度的影响,造成倾角传感器测量信号中含有较多噪声信号,测量误差大,难以利用直接测量的倾角信号估计足端位置。为了更好地得到精确的倾角信号,本文采集了倾角传感器输出的温度信号,把温度信号和经过卡尔曼滤波方法滤波后的信号作为建立的基于蚁群聚类算法的RBF神经网络模型的样本数据,对传感器倾角信号进行温度补偿。经过实验验证,能够很好地去除倾角传感器信号中的噪声,对倾角信号进行温度补偿,使得测量误差能够控制在0.75%以内,为估计足端位置提供了高精度的角度值。

参考文献:

[1] 赵杰,张赫,刘玉斌,等. 六足机器人HITCR-I的研制及步行实验[J]. 华南理工大学学报(自然科学版),2012,40(12):17-23.

[2] 朱月青,张志利,谭立龙,等. BP神经网络在倾角传感器数据融合中的应用[J]. 仪表技术与传感器,2010(1):101-102.

[3] 邵晓敏. 全量程无线倾角传感器设计[D]. 上海:上海大学,2012.

[4] 曹建安,张乐平,吴昊,等. 采用倾角传感器实现空间旋转角度测量的解析方法研究[J]. 西安交通大学学报,2013,47(10):109-114.

[5] 袁健,周忠海,金光虎,等. 基于卡尔曼滤波的自主式水下航行器大尺度编队控制[J]. 智能系统学报,2013(4):344-348.

[6] 王小冬. 卡尔曼滤波在卫星导航中的应用研究[D]. 大连:大连海事大学,2008.

[7] 罗贞. 基于卡尔曼滤波器的系统状态估计和故障检测[D]. 武汉:华中科技大学,2013.

[8] 乃永强,李军. 基于极限学习机的机械臂自适应神经控制[J]. 信息与控制,2015,44(3):257-262.

[9] 乔俊飞,韩红桂. RBF神经网络的结构动态优化设计[J]. 自动化学报,2010,36(6):865-872.

[10] 张朋,范福玲,杨益,等. 基于时间序列模型的超声信号滤波算法研究[J]. 传感技术学报,2015(3):396-400.

[11] 郑立斌,王红梅,顾寄南,等. RBF神经网络在机器人视觉伺服控制中的应用[J]. 机床与液压,2015,43(15):41-43.