信息化背景下小组合作式教学在中职数学中的应用

古乐娟

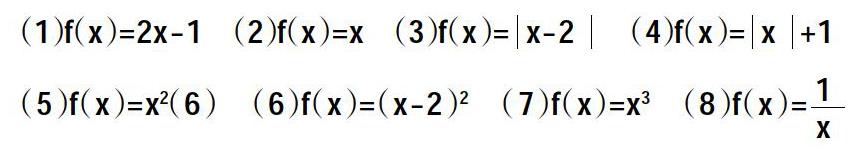
[摘           要]  随着信息化时代的到来，以信息技术为支持的现代化教育模式赋予了课堂新的形式。以“函数的奇偶性”为例，以问题为导向，采用“任务驱动”教学法，用小组合作的教学形式，由问题的层层递进引发学生思考，在讨论和交流中获得共识。重点从课前准备、课堂实施、课后提升三个方面，阐述如何借助信息技术激发学生的学习热情，促进学习自主化，实现高效课堂。

[关    键   词]  信息化;小组合作;中职数学

[中图分类号]  G712                [文献标志码]  A                    [文章编号]  2096-0603（2018）35-0230-02

一、信息化教学背景

在科技进步飞速发展的今天，将信息技术融入中职数学的教学中势在必行。函数的奇偶性是中职数学课程中的重要概念之一，其理论抽象，概念的理解对学生来说难度很大。通过使用云班课、慕课、微课、几何画板、多媒体课件等信息化教学手段，使学生课前通过自主学习，达到复习旧知、预习新知的目的;课上几何画板的使用化解了学生对函数奇偶性概念的理解;课后把相关的慕课、微课、多媒体课件等学习资源发送到云班课共享，学生根据个人情况加以复习巩固，有疑问可以互相讨论或者向老师求解答疑，还有中国大学MOOC、中职资源网扩大学生知识的广度和深度。信息化背景下，教学打破了时空限制，不仅有利于增加课堂容量，而且提高了学生的学习兴趣和学习效率。

二、课前准备

（一）教师

1.借助云班课，构建班级交流群。

2.发布“几何画板”微视频，要求学生完成8个函数图像。

3.“点的对称”慕课，设计课前任务单，由课代表收回。对“收获”和“疑问”进行统计，发现90%的学生掌握了坐标轴内点的对称性。

4.分组，按组间同质、组内异质将学生分成4个组;制定学习评价表。

（二）学生

1.下载并上传对称图形到云班课班级交流群。

2.学习微课，绘制8个函数图像，分别是：

（1）f（x）=2x-1 （2）f（x）=x （3）f（x）=x-2 （4）f（x）=x+1

（5）f（x）=x2（6） （6）f（x）=（x-2）2 （7）f（x）=x3 （8）f（x）=

3.学习慕课，完成课前任务单，尤其是“收获”和“疑问”。

在课前准备中，学生通过慕课的学习，对图形的对称进行了复习，为课上学习函数图像的对称性奠定了基础;同时提高了学生的动手能力和使用信息化的手段参与课堂的能力。

三、课堂实施

（一）创设情境，导入新课

教师整理学生上传的对称图片并制作成电子相册，学生在欣赏到美的同时归纳出对称图形的类型：轴对称和中心对称。各自的特点：轴对称图形是沿对称轴折叠，两侧图形完全重合;中心对称图形是绕中心点旋转180度，旋转前后图形可以完全重合。接下来学生把8个函数分成三类：（1）关于y轴对称：f（x）=x+1，f（x）=x2;（2）关于原点中心对称：f（x）=x2，f（x）=x3，f（x）=;（3）既不关于y轴又不关于原点对称：f（x）=2x-1，f（x）=x-2，f（x）=（x-1）2。

教师提出问题：“同学们，图像对称与函数的奇偶性之间有怎样的联系？”

在第一环节，通过生活中的对称过渡到函数图像的对称，在创设轻松愉快的探索情境中，激发了学生的学习兴趣，使学生更快地融入课堂。教师问题的提出，使学生在充满疑惑的眼神中进入第二环节。

（二）布置任务，分组讨论

因为奇函数、偶函数是并列概念，知一会二，所以，任务一：一、三组讨论关于y轴对称的函数图像;任务二：二、四组讨论关于原点中心对称的函数图像。学生带着问题先进行自主探究，然后組内、组间互助。学生在讨论时，教师参与其中，（1）对存在问题的学生，给予指导;（2）对后进生，发现他们身上的闪光点并进行肯定;（3）对学有余力的学生，引导他们思考第三类图形的特点。

在这二环节，从函数图像的对称，到对称点的坐标特征，从特殊到一般，引导学生在小组交流讨论的过程中，归纳概念，加深学生对奇函数和偶函数的理解。

（三）小组汇报，展示成果

1.一组代表汇报，先用几何画板演示3对关于y轴对称的点坐标，再用列表法从代数式的角度观察x=±1，±2，±3时，函数值的结果。

从而初步得出：关于y轴对称的函数图像，当自变量互为相反数时，函数值相同，学生对一组代表的发言进行评价。

2.一组成员补充。用几何画板动态演示一对坐标点变化，观察函数f（x）=x2，发现：随着这一对坐标的变化，虽然横坐标互为相反数，但对应纵坐标的值相等。初步形成偶函数的概念：关于y轴对称的图形，对于任意x值，都满足f（-x）=f（x），这时，称函数f（x）为偶函数。

3.三组学有余力的学生探究第三类图形：既不关于y轴又不关于原点对称的特点，发现：定义域不关于原点对称，三组学生的创新意识值得肯定。

接下来，在二组代表汇报、二组成员补充、四组补充下，奇函数的概念也水到渠成地概括出来，即：关于原点对称的图形，对任意x值，都满足f（-x）=-f（x），这时，称函数f（x）为奇函数。尤其在这一环节，四组补充了3点：（1）第四类函数：既是奇函数又是偶函数;（2）定义域关于原点对称是函数具有奇偶性的共同前提;（3）观察多个奇函数的解析式（如f（x）=x2，g（x）=x3，h（x）=x，q（x）=x-1），发现指数为奇数，大胆推测奇函数名称的由来（当函数指数为奇数时，该函数为奇函数），这为后面学习幂函数的奇偶性埋下伏笔。四组学生的创新值得大家学习。

在这一环节，学生是自己经历定义得出了结果，而不是由教师直接得出，符合由浅入深的认知规律，培养了学生思维的严谨性，提高了学生的合作能力、创新意识，体会到了成功的乐趣，进一步理解了函数奇偶性的概念，解决了本节课的教学重点，突破了教学难点;但是学生的定义不够完善，需要教师进一步进行补充和对定义进行深入的剖析。

（四）应用举例，巩固新知

例1：根据函数图像，判断函数的奇偶性，强调定义域关于原点对称是函数具有奇偶性的前提。

例2：给定函数解析式，判断函数的奇偶性，从“图像”和“定义”两种方法解决。这有助于：（1）渗透数形结合思想。（2）规范书写步骤，即两判一求一结论。

接下来，学生到黑板答题，由同学批改，教师对出错率高的题目重点讲解;学生到云班课答题，根据及时反馈系统，90%的学生掌握了新知，提高了做题能力，其他学生做基础题继续巩固练习。

在这四环节，学生自己总结出函数奇偶性判断的两种方法，对奇偶性的理解更为深刻;通过对例题的讲解，加深学生对两种判断方法的理解;学生在“云班课”的环境中进行课堂练习，便于及时向老师反馈信息，也利于老师对教学效果进行评价和及时采取应对措施。

（五）归纳总结，布置任务

1.学生先总结，教师后补充。

2.分层布置作业，与生活、专业相联系，评选优秀作品。使不同层次的学生都可以获得成功的喜悦，看到自己的潜能，进而激发学习兴趣。

3.线上，云班课的经验值;线下，评价表，通过自评、互评、师评，尤其是“创新点”的评价，综合评价可以使学生得到客观公正的评价，让学生了解自己的综合表现，增强团队合作意识，在肯定自己的同时，明确努力的方向;课下，学生在云班课留言，对老师评价，改进教学。

四、课后提升

（一）通过课后慕课学习，可以弥补学生对课堂内容掌握的不足。

（二）通过云班课向学生推送资源，贯彻“终身学习”的教学理念。

（三）通过登录中职教学资源网进行课后学习，可以开阔学生的眼界，扩大知识面。

五、教学反思

（一）学生的亲历体验。学生在亲历几何画板作图，讨论图像间的关系及动态演示等一系列的体验中，更真切地建构了数学知识。

（二）软件几何画板改变了传统的列表、描点、连线的作图方式，动静结合，生动直观，有效突破了本节课的教学难点。

（三）云班课不仅便于师生之间互动，及时反馈学生的学习效果，而且增强了学生的动手能力，提高了他们对课堂的参与度。

（四）小组合作学习，较好地达成了本课的教学目标。

（五）数学建模思想。通过生活中的问题，发展学生数学建模、数据分析的学科核心素养，为专业课的学习铺平道路。

（六）存在的不足。由于采用小组合作学习，教师注意了组间同质、组内异质，关注了后进生的参与度，但因个别学生数学基础薄弱，无法融入小组讨论，产生了依赖思想。下一步打算用结对帮扶的方法促进他们发展，渐渐产生学习动力。

六、结语

信息化教学已成为现代教育发展的必然趋势，信息化技术融入教学中，一方面，挖掘学生的学习潜力，培养学生的探究能力、合作能力，提高学生的创新能力;另一方面，师生之间、生生之间的交互式学习由课上延伸到课下，不再只限于课堂上，有助于学生利用碎片化时间积极主动地巩固新知，化解疑问，培养学习兴趣。这也正是中职数学教学过程中运用各种信息化技术的价值所在。当然，中职数学在信息化背景下，小组合作式教学仍存在各种各样的问题，还需要师生共同努力，找方法解决。

参考文献：

[1]王雅萍.高職数学信息化教学探索：以定积分的概念为例[J].安微电子信息职业技术学院学报，2017，16（5）：52-54.

[2]陈小兵.中职数学信息化教学中的困惑与思考[J].内蒙古教育（职教版），2014（12）：81.

[3]高雷.从优质课展评看中职数学信息化教学手段的运用[J].中国教育技术装备，2015（11）：85-86.

[4]袁蕾.信息化背景下小组合作式教学的教学设计：以职教数学中的三角函数诱导公式为例[J].教育教学论坛，2018（32）：253-255.