直升机滑跑地面共振特性研究

魏 钢，刘湘一，宋山松，王立国

（1.海军驻汉中地区航空军事代表室，陕西汉中723000；2.海军航空大学，山东烟台264001；3.92955部队，辽宁葫芦岛125000）

直升机在高原地区进行超载起飞和着陆时，经常要进行地面滑跑[1]。滑跑时，直升机除了可能发生机轮摆振[2-3]外，机轮的侧向刚度会随滑跑速度的提高而降低，从而降低机体侧向模态固有频率[1，4]。对于大重量时，直升机侧向二阶模态固有频率较低的情况[5]，该阶模态固有频率的降低，可能会使原来高于旋翼工作转速的不稳定边界落到工作转速以内而发生地面共振[6]。另一方面，驾驶杆纵向周期变距操纵以及滑跑速度造成的旋翼不对称来流，使桨叶产生周期性挥舞和摆振运动，引起旋翼阻尼器周期振动[7]。滑跑过程中一旦发生扰动，阻尼器将处于“双频”条件下工作，其等效阻尼会严重下降[8-9]。

相对于停机状态，直升机定常滑跑时动力学特性分析更为复杂，除考虑操纵与滑跑速度影响外，还需考虑起落架与旋翼阻尼器非线性特性。Lee Yoon Kyu等[10-11]就起落架非线性问题进行了讨论；杨礼芳等[12]也分析了轮胎刚度对起落架缓冲及滑行操纵性能的影响；张文静[13]对直升机非线性“地面共振”进行了详细分析研究。对滑跑地面共振问题，米里计算得到不稳定区降低约 20%～30%[4]；Rebecca A Snyder等[14]对单、双频正弦激励下阻尼器非线性特性进行了研究，验证了双频激振下的旋翼减摆器的复模量较单频条件下会明显下降，这对旋翼/机体耦合动稳定性带来不利影响[15]。上述计算采用了部分飞行状态量来替代滑跑状态量，与滑跑实际是存在一定的误差。许勤勇等[16]对直升机地面滑跑进行飞行力学分析，给出了不同滑跑速度的操纵建议，但未考虑滑跑时的地面共振问题。

本文基于定常滑跑平衡特性分析仿真结果[17]，求得定常滑跑下的旋翼阻尼与机体模态特性，结合起落架的静、动特性试验数据，对直升机滑跑地面共振进行更为准确的研究分析。

1 定常滑跑时机体动特性分析

滑跑过程中，机体固有特性会发生明显变化，假设机身为刚体，则其特性取决于具有非线性特性的弹性起落架（缓冲支柱和机轮组成）。将机体独立为纵、横向模态，可计算出不同滑跑速度下的机体特性，文中主要分析机体的横滚模态。

1.1 机体横向模态固有特性

前三点式起落架垂向特性需要考虑缓冲支柱与机轮串联，而各起落架有2个机轮，则起落架垂向刚度、阻尼分别为：

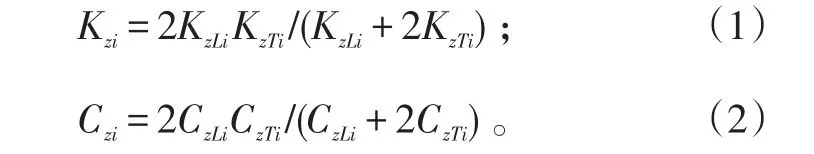
式（1）、（2）中：i=1,2,3分别表示3个起落架，下同；KzLi和CzLi表示缓冲支柱的垂向等效刚度和阻尼；KzTi和CzTi表示机轮垂向等效刚度和阻尼。

假设机轮处于纯滚动状态，则不考虑其纵向特性。起落架侧向刚度、阻尼系数与缓冲支柱联系不大，因而仅需考虑2个机轮等效并联的侧向固有特性。由文献[4]得到起落架侧向刚度和阻尼与滑跑速度的关系：

式（3）、（4）中：K′yi和C′yi表示停机时机轮的侧向等效刚度、阻尼，根据文献[17]与试验数据进行插值；v为滑跑速度；r为机轮半径，本文取0.32 m；ω为机轮侧向振动频率，随滑跑速度变化需不断迭代。

根据图1机体物理模型，建立机体横向平移与滚转的无阻尼自由振动方程：

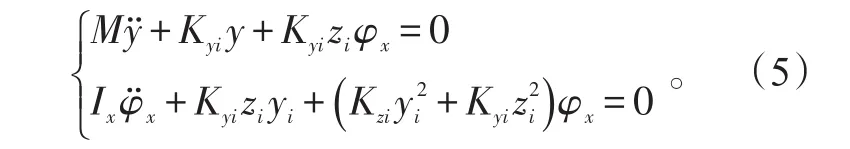
式（5）中：yi和zi分别为起落架到机体重心横向和垂向距离；M为机体质量；φx为机体滚转角。

图1 机体侧向和纵向物理模型Fig.1 Physical model of fuselage lateral and longitudinal

依据文献[7]对方程（5）求解，可得机体横向无阻尼下的两阶固有频率ω1和ω2。设瞬心的坐标位置为z0，当无阻尼系统以某阶模态振动时，由瞬心处的侧力平衡关系式（6）可得两频率对应的瞬心位置，进而区分两振型所对应频率。

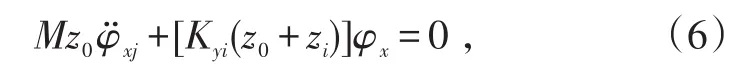
式中，φxj=φxjsin(ωjt+θj)，j=1,2分别表示机体横向前两阶模态，下述相同。

在此基础上，由文献[7]当量化准则得到桨毂中心的机体横向当量特性，各当量参数为：

式（7）中：My、Ky、Cy分别为当量质量、当量刚度、当量阻尼；Ix为绕x轴惯性矩；zh为重心到桨毂中心距离。

1.2 机体固有特性分析

取旋翼工作转速为212rpm，起始迭代激振频率为4Hz，由式（2）得到起落架侧向等效刚度随滑跑速度变化规律如图2所示。

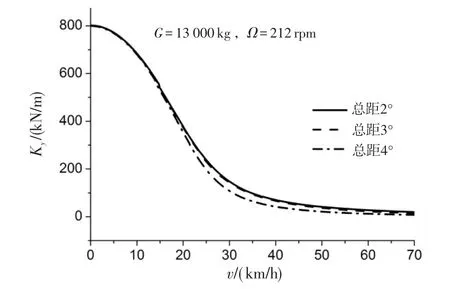
图2 不同旋翼总距下机体侧向刚度Fig.2 Fuselage lateral stiffness with different collective pitch

由图2可知，起落架侧向刚度特性受滑跑速度影响较大，在10～30km/h间起落架侧向刚度下降较快，近70%，而旋翼总距增加会使侧向刚度略微减小。

求解无阻尼自由振动方程，得到不同滑跑速度下机体侧向两阶模态固有频率变化规律如图3所示。

图3 不同旋翼总距下机体侧向模态频率Fig.3 Fuselage lateral mode frequency with different collective pitch

由图3可知，随着滑跑速度增加，机体侧向两阶模态固有频率均逐渐减小，而不同旋翼总距下整体变化趋势一致；旋翼总距为2°时，滑跑速度在10～30km/h时，机体侧向高阶模态固有频率从3.83Hz减小到2.26Hz，幅度减小达41.0%，低阶模态固有频率在此速度区间也大幅减小，减小达58.5%；随旋翼总距增加，滑跑过程中会使高阶模态固有频率减小量进一步加大。图4与图5给出了机体横向当量特性随滑跑速度变化规律。

图4 不同旋翼总距下机体侧向模态当量刚度Fig.4 Fuselage lateral mode equivalent stiffness with different collective pitch

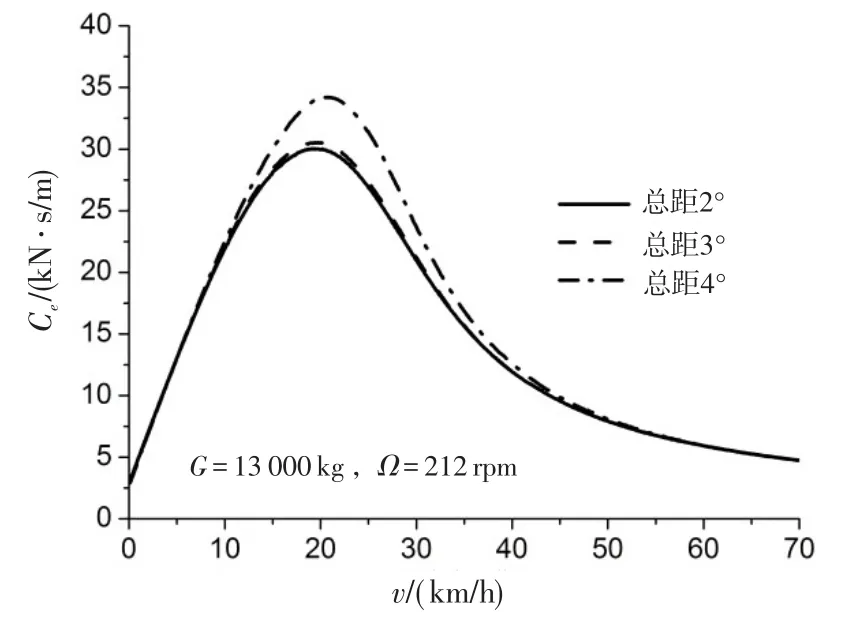
图5 不同旋翼总距下机体侧向模态当量阻尼Fig.5 Fuselage lateral mode equivalent damping with different collective pitch

由图4、5可知，不同旋翼总距下当量特性变化差别并不大。其中，低总距下当量阻尼在滑跑速度10～40km/h内略微减小，而低总距下当量刚度在滑跑速度超过25km/h后略微增加。

2 定常滑跑时机阻尼器特性分析

2.1 定常滑跑下旋翼阻尼分析模型

球柔性旋翼桨叶的挥舞、变距和摆振等运动可以由弹性球轴承的变形来实现，省去了各类复杂铰接结构，然而阻尼器与桨叶运动之间却产生了几何耦合，阻尼器的轴向位移、速度及载荷等特性由上述运动共同决定。计入几何耦合的阻尼器模型如图6所示[18]。

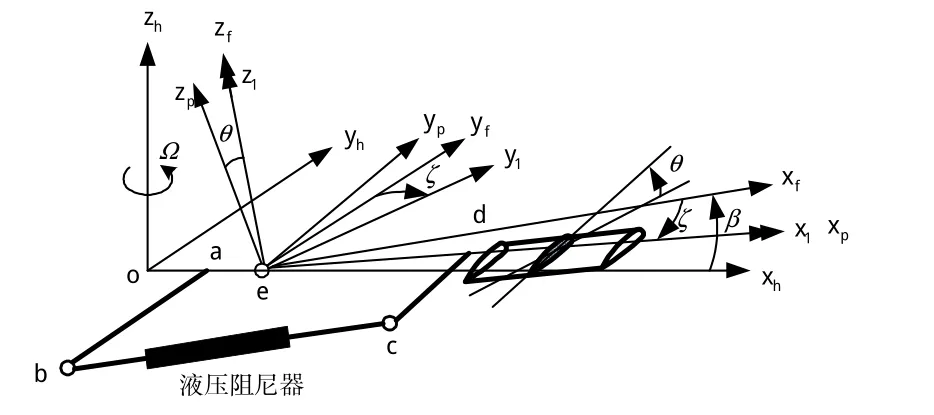
图6 计入几何耦合的阻尼器模型Fig.6 Damper model with geometrical coupled

图6中，阻尼器bc在桨毂旋转坐标系中的矢量为：

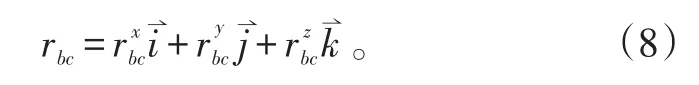
图7所示为某型液压阻尼器力-速度的实验数据曲线。

图7 旋翼阻尼器力-速度曲线关系Fig.7 Rotor damper force-velocity curve relationship

对旋翼阻尼器位移求导得到其轴向速度后，可以根据如图7所示的力-速度曲线确定作用力为：

vd单位为m/s。假定忽略各运动副间的摩擦力，结合阻尼力在球柔性轴承处对机体产生的阻尼力矩，整理得到桨叶摆振动力学方程：

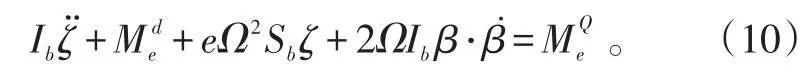
式（9）中：β和ζ分别为桨叶的挥舞和摆振角；Ib和Sb分别为桨叶绕垂直铰质量惯性矩和静矩；Ω为旋翼转速；为气动力矩。

滑跑时，旋翼处于周期性挥舞及摆振运动，会引起旋翼液压阻尼器定常的强迫振动。假设设1Ω谐波背景振动幅值为x0，取扰动量幅值为δ，两运动间相位差为φ0，ωζ为桨叶摆振固有频率，则“双频”激振下作用在阻尼器上的位移表示为：

阻尼器位移求导得到阻尼器速度v，然后通过“单频”条件的力-速度曲线得到阻尼力F(v)。根据实际系统与等效线性系统在振动一周内吸收能量相等的原理，由此得到等效线性阻尼：

式（11）中，W为实际非线性阻尼器振动一周内吸收的能量。

2.2 滑跑速度、旋翼总距对旋翼阻尼影响

由式（10）得摆振角，经文献[17]转换得到定常滑跑下旋翼阻尼器行程x的峰值xd的变化规律，见图8。

图8 不同条件下阻尼器的轴向位移稳态峰值Fig.8 Axial displacement steady amplitude of damper in different cases

由图8可知，旋翼总距增加会明显增加旋翼阻尼器稳态振动位移，但由于旋翼各自由度运动耦合，其稳态振动位移受滑跑速度影响较小。

当直升机出现扰动时旋翼阻尼器将处于“双频”激励状态，而上述其稳态振动位移变化为1Ω背景振动幅值、阻尼器行程提供了依据。不同扰动量时旋翼阻尼器“双频”条件下等效阻尼与其“单频”下试验值如图9所示。由图9可知，旋翼液压阻尼器“单频”阻尼值小扰动量（δ＜0.01 m）下明显大于“双频”等效值，其“双频”激励状态下等效阻尼减小幅值存在超过50%的情况；扰动量增加，“单频”和“双频”条件下等效阻尼差异逐渐减小，大扰动量时，背景振动量的影响逐渐降低，两者近似一致；小扰动量下，旋翼总距增加会使得等效阻尼下降得更小。

图9 不同条件下液压阻尼器等效阻尼特性Fig.9 Equivalent damping for hydraulic damper in different cases

3 直升机地面滑跑地面共振分析

3.1 滑跑速度对地面共振稳定性分析

依据上述定常滑跑下机体及旋翼液压阻尼器动特性，求解旋翼/机体耦合振动系统的运动方程[7]，特征值实部见图10，其负值表示模态阻尼σ。

图10 有旋翼阻尼旋翼/机体耦合模态阻尼Fig.10 Rotor/fuselage coupled modal damping with rotor damping

由图10可知，旋翼总距2°时，取较大扰动量（δ=26mm），停机状态下，直升机不会发生地面共振，且设计留有足够的阻尼裕度（21.7%）。

相同条件下，模态频率ωs（特征值虚部）、模态阻尼随滑跑速度变化见图11、12。图11可知，LA和LR模态频率大致保持在 4.75Hz（LA）和2.6Hz（LR），BP模态频率同样随滑跑速度变化较小，这是由于机体纵向特性受滑跑速度影响较小；滑跑速度会导致机体侧向模态固有频率降低，随滑跑速度增加，BR模态频率则会逐渐减小，而由于与旋翼耦合计算，BR模态频率较图3会有减小；当滑跑速度为20～32km/h时，BR与LR模态出现了危险的耦合区，两模态频率相等。

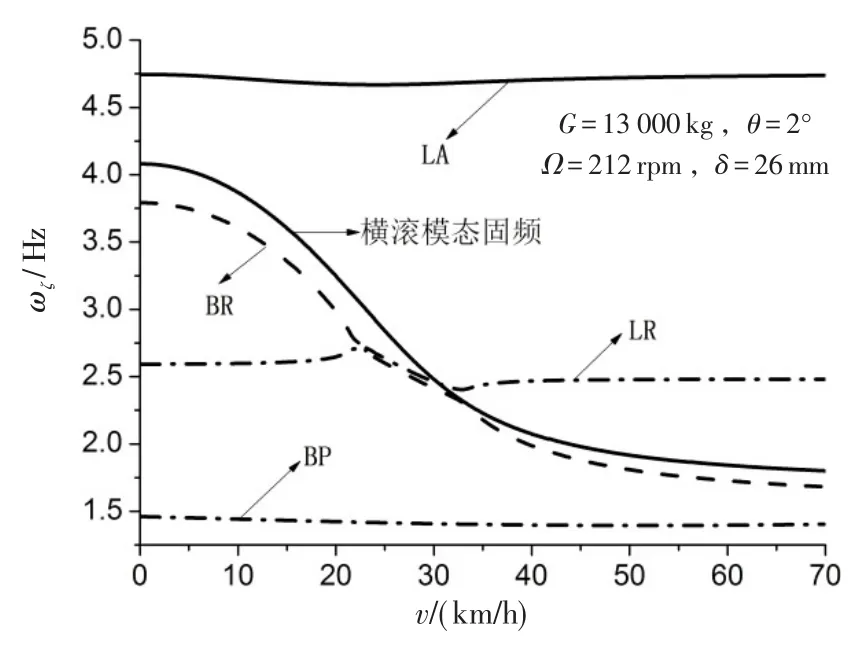
图11 有旋翼阻尼下不同滑跑速度耦合模态频率Fig.11 Coupled mode frequency at different running speed with rotor damping

图12 有旋翼阻尼下不同滑跑速度耦合模态阻尼Fig.12 Coupled mode damping at different running speed with rotor damping

由图12可知，当滑跑速度处在122.8～31.6km/h时，LR模态模态阻尼大于0，系统是处于不稳定状态，而其他模态均处是小于0，系统稳定。综上，旋翼总距2°（扰动量δ=26mm）时，直升机在滑跑速度122.8～31.6km/h区间内会发生地面共振，地面滑跑应避免进入该速度区间。

为进一步分析直升机滑跑过程中地面共振产生机理，取滑跑速度25km/h，进行具体分析，得到模态频率、模态阻尼变化规律如图13、14所示。

由图13可知，出现了BR与LR模态频率相等情况，其对应旋翼转速范围为：106～127rpm和195～255rpm，且旋翼工作转速包含在其中。由图14可知，在旋翼转速200～256rpm区间内，LR模态阻尼始终大于0，系统处于不稳定状态，其他情况下则处于稳定状态。在旋翼总距2°（扰动量δ=26mm）时，停机时有足够裕度设计的直升机滑跑过程中会出现地面共振，且在包含旋翼工作转速在内的一定转速区间内，旋翼/机体耦合系统均是不稳定的，滑跑速度对地面共振稳定性影响较大。

图1325 km/h下模态频率随旋翼转速变化图Fig.13 Modal frequency changes following rotor speed at25km/h

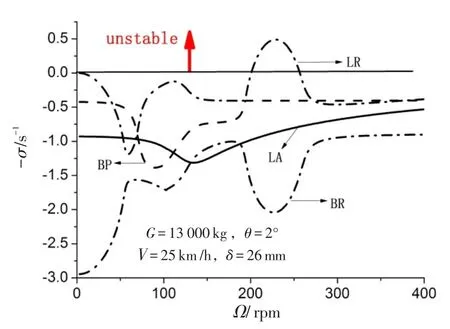
图1425 km/h下模态阻尼随旋翼转速变化图Fig.14 Modal damping changes following rotor speed at25km/h

3.2 旋翼总距对滑跑地面共振稳定性分析

定常滑跑时，由图9可知，不同总距下旋翼液压阻尼器“双频”等效阻尼，1.2节给出了不同总距下机体当量特性，分别代入平面动力学模型计算分析，以危险的旋翼摆振后退型模态（LR）分析旋翼总距对滑跑地面共振影响，大扰动量（δ=26mm）的结果如图15所示。大旋翼总距失稳时其滑跑速度范围减小，不稳定性有所降低。这是由于旋翼阻尼近似一致情况下，大旋翼总距下机体侧向模态当量阻尼较大；由于旋翼总距增加会减小机体固有频率，大旋翼总距下不稳定区滑跑临界速度则减小。

中等扰动量（δ=15mm）时，不同旋翼总距下依旧存在不稳定区，而当扰动量减小，耦合系统不稳定性会降低，图16中不稳定区结果较图15降幅约50%，不稳定区滑跑速度范围减小。此时，旋翼总距的影响与大扰动量时相一致，文中不再赘述。

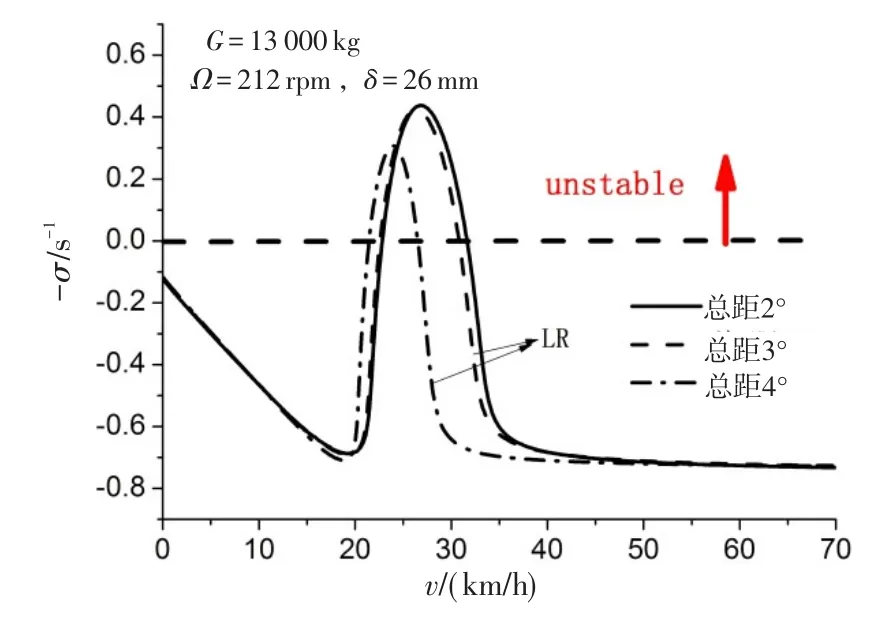
图15 大扰动量下LR模态阻尼随滑跑速度变化图Fig.15 LR modal damping changes with running speed under large disturbance

图16 中等扰动量下LR模态阻尼随滑跑速度变化图Fig.16 LR modal damping changes with running speed under medium disturbance

图17给出小扰动量（δ=7.5mm）下LR模态阻尼随滑跑速度变化情况。小扰动量下，耦合系统会有足够的旋翼阻尼吸收振动，图中显示小总距滑跑过程中系统始终稳定，不会发生地面共振；而随旋翼总距增加，稳定性逐渐降低，又出现系统失稳的滑跑速度区间，原因是旋翼阻尼动特性受旋翼总距变化的影响。

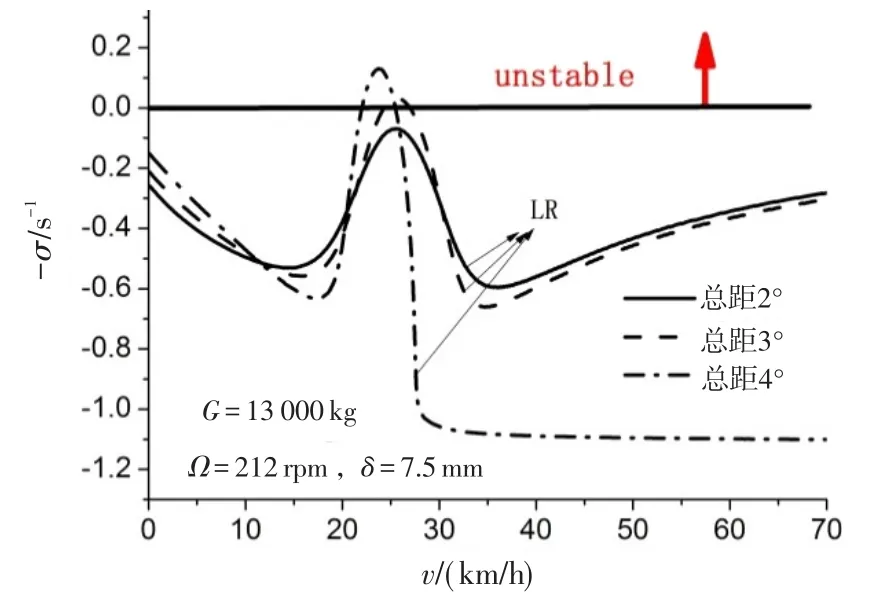
图17 小扰动量下LR模态阻尼随滑跑速度变化图Fig.17 LR modal damping changes with running speed under small disturbance

4 结论

本文综合定常滑跑时机体及阻尼器动特性分析，计算球柔性旋翼直升机滑跑地面共振稳定性，分析了不同滑跑速度与旋翼总距对其影响规律，结果显示：

1）直升机滑跑速度与旋翼总距对机体动特性影响主要体现在其侧向模态频率的降低；滑跑速度还会降低机体当量特性，而旋翼总距对其影响相对较小。

2）停机状态下阻尼裕度足够的直升机，滑跑过程中可能出现地面共振，但在小总距、小扰动下依旧不会发生地面共振。

3）定常滑跑时，旋翼总距增加，系统不稳定性增加，且不稳定区滑跑临界速度会略微降低。为保证安全训练任务，建议直升机滑跑采用小总距操纵，滑跑速度限制在15km/h以下。

[1]航空航天工业部科学技术研究院.直升机动力学手册[M].北京：航空工业出版社，1991：324-332.INSTITUTE OF SCIENCE AND TECHNOLOGY OF MINISTRY OF AEROSPACE INDUSTRY.Helicopter dynamics manual[M].Beijing：Aviation Industry Press，1991：324-332.（in Chinese）

[2]诸德培.摆振理论及防摆措施[M].北京：国防工业出版社，1984：1-24.ZHU DEPEI.Shimmy theory and suppressing measure[M].Beijing：National Defense Industry Press，1984：1-24.（in Chinese）

[3]熊程刚.直升机旋翼-起落架系统动力学特性分析研究[D].南京：南京航空航天大学，2013.XIONG CHENGGANG.Analysis of dynamic characteristics for helicopter’s landing gear-rotor system[D].Nanjing：Nanjing University of Aeronautics&Astronautics，2013.（in Chinese）

[4]米里.直升飞机计算和设计（第二卷）：振动和动强度[M].北京：国防工业出版社，1976：230-236.MI LI.Helicopter calculation and design（the second volume）：vibration and dynamic strength[M].Beijing：National Defense Industry Press，1976：230-236.（in Chinese）

[5]胡国才，刘湘一，刘书岩，等.舰面状态直升机机体在起落架上的固有频率分析[J].海军航空工程学院学报，2012，27（6）：639-644.HU GUOCAI，LIU XIANGYI，LIU SHUYAN，et al.Anal-ysis of helicopter natural frequencies on landing gear at ship-borne conditions[J].Journal of Naval Aeronautical and Astronautical University，2012，27（6）：639-644.（in Chinese）

[6]胡国才，魏钢，吴靖.滑跑速度对直升机侧向刚度模态频率的影响[J].南京航空航天大学学报，2016，48（4）：516-521.HU GUOCAI，WEI GANG，WU JING.Effect of running velocity on helicopter lateral mode frequency[J].Journal of Nanjing University of Aeronautics&Astronautics，2016，48（4）：516-521.（in Chinese）

[7]张晓谷.直升机动力学设计[M].北京：航空工业出版社，1995：80-99.ZHANG XIAOGU.Helicopter dynamics design[M].Beijing：Aviation Industry Press，1995：80-99.（in Chinese）

[8]胡国才，向锦武，张晓谷.黏弹减摆器非线性特性对直升机前飞空中共振的影响分析[J].航空学报，2005，26（2）：199-202.HU GUOCAI，XIANG JINWU，ZHANG XIAOGU.Analysis of the effect of nonlinear characteristics of elastomeric lag damper on helicopter air resonance in forward flight[J].Journal of Aviation，2005，26（2）：199-202.（in Chinese）

[9]吴靖，胡国才.带定压活门的液压阻尼器力学性能研究[J].华中科技大学学报，2017，45（2）：44-49.WU JING，HU GUOCAI.On mechanical features of hydraulic damper with pressure relief valve[J].Journal of Huazhong University of Science and Technology，2017，45（2）：44-49.（in Chinese）

[10]LEE Y K，KIM K J.Effects of landing gear nonlinearities on ground resonance of helicopter[C]//14thInternational Congress on Sound and Vibration，Caims：International Institute ofAcoustics and Vibration.2007：1693-1699.

[11]MONTERRUBIO L，SHARF I.Influence of landing-gear design on helicopter ground resonance[J].Canadian Aeronautics and Space Journal，2002，48：133-144.

[12]杨礼芳.飞机轮胎刚度及尾轮摆振仿真分析[D].南京：南京航空航天大学，2012.YANG LI FANG.The simulation analysis on the tire stiffness and tail-wheel shimmy of a aircraft[D].Nanjing：Nanjing University of Aeronautics&Astronautics，2012.（in Chinese）

[13]张文静.直升机非线性“地面共振”分析研究[D].南京：南京航空航天大学，2010.ZHANG WENJING.Analysis of nonlinear helicopter ground resonance[D].Nanjing：Nanjing University of Aeronautics&Astronautics，2010.（in Chinese）

[14]REBECCA A S，RAMKUMAR K，NORMAN M W.Mechanisms-based analysis for elastomerical lag damper behavior under single and dual frequency excitation[C]//AIAA Applied Aerodynamics Conference.AIAA，2001：1537.

[15]FELKER F F，LAU B H，MCLAUGHLIN S，et al.Nonlinear behavior of an elastomeric lag damper undergoing dual-frequency motion and its effect on rotor dynamics[J].Journal of the American Helicopter Society，1987，34（4）：45-53.

[16]许勤勇，殷士辉，徐玉貌.直升机地面滑跑飞行力学研究[J].直升机技术，2015（2）：6-10.XU QINYONG，YIN SHIHUI，XU YUMAO.Flight dynamics analysis of helicopter taxiing[J].Helicopter Technique，2015（2）：6-10.（in Chinese）

[17]魏钢，胡国才，吴靖.直升机地面滑跑平衡特性研究[C]//第33届直升机年会.景德镇：中国航空学会直升机分会，2017：89-94.WEI GANG，HU GUOCAI，WU JING.Analysis of helicopter running balance features[C]//33thHelicpter Society.Jingdezhen：Helicopter Branch of Chinese Society of Aeronautics andAstronautics，2017：89-94.（in Chinese）

[18]胡国才.减摆器非线性特性及其对直升机旋翼/机体耦合动稳定性影响研究[D].北京：北京航空航天大学，2003.HU GUOCAI.Nonlinear characteristics of blade lag dampers and its effect on helicopter rotor/airframe coupled dynamic stability[D].Beijing：Beijing University of Aeronautics&Astronautics，2003.（in Chinese）