ARIA分组密码算法的不可能差分攻击

谢高淇 卫宏儒

(北京科技大学数理学院 北京 100083) (xiegaoqi@sina.cn)

ARIA密码算法[1]是韩国国家安全研究所提出的一种SPN(substitution-permutation network)结构[2]的密码算法，隶属于分组密码算法[3]，在2004年时，韩国工业部、商业部和能源部确定ARIA为韩国分组密码算法标准.在结构上，ARIA密码算法和AES(advanced encryption standard)算法[4-5]很相似，故很多用来分析AES算法的分析方法可以用来对ARIA密码算法进行分析，并取得了很好的效果.本文类比对AES算法的分析，结合对ARIA密码算法的研究，实现对ARIA密码算法新的攻击.

从文献[6-7]可知，不可能差分分析方法是由Biham和Knudsen提出的，一种使用不可能出现的差分即概率为0的差分特征过滤错误密钥猜测，从而得到正确密钥值的分析方法.一经提出，该方法便得到了广泛的应用，被应用于分析密码结构与算法.尤其是对AES算法的分析中效果良好，ARIA密码算法和AES算法结构上相似，不可能差分分析针对ARIA密码算法的分析也取得了非常好的效果.

1 算法ARIA

1.1 符号说明

本文所使用符号具体释义如表1所示：

Table 1 Symbol Description表1 符号说明

1.2 ARIA算法介绍

ARIA密码算法是SPN结构型分组密码，分组长度为128 b，密钥长度为128 b,192 b,256 b，相应的轮数分别为12轮、14轮和16轮[8].128 b的数据分组对应一个4×4的表格，共16 B，如图1所示.

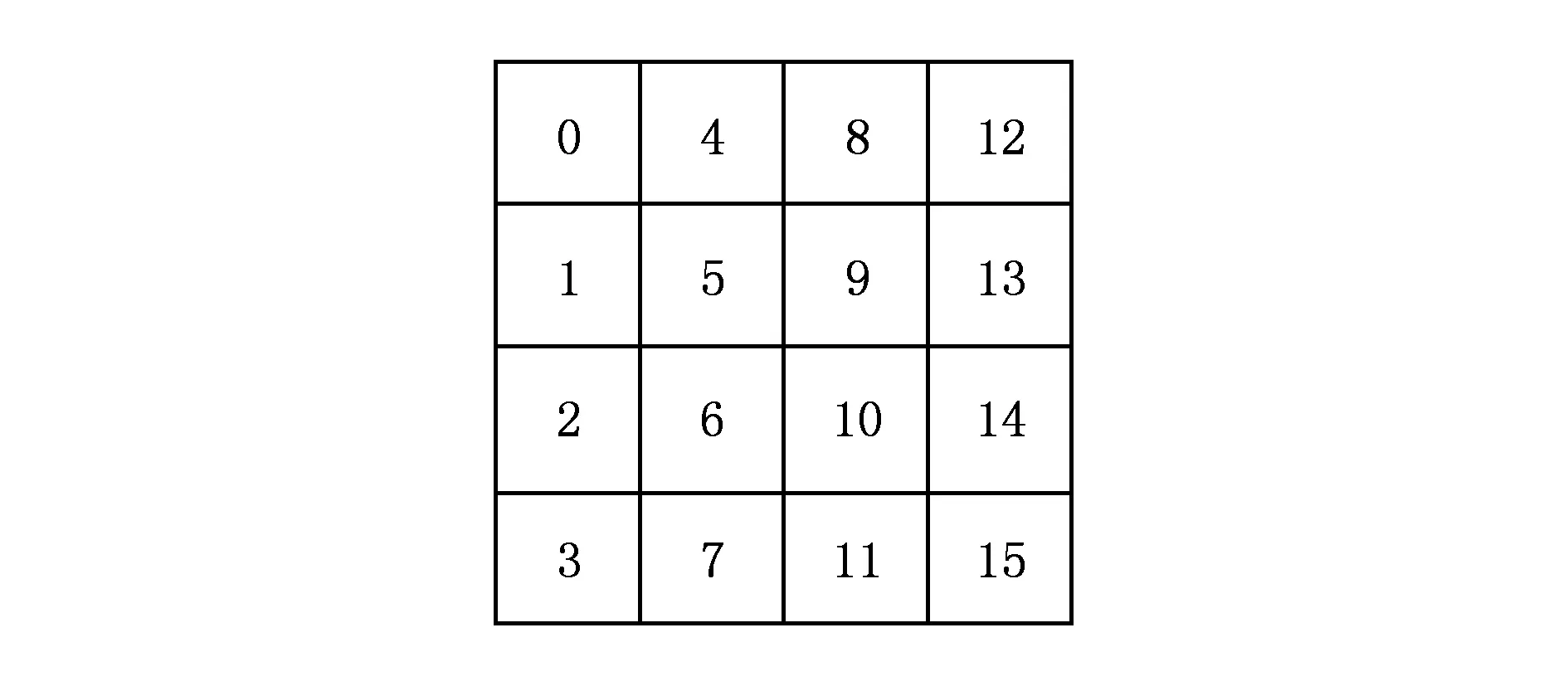
Fig. 1 The state of 128 b on ARIA图1 ARIA的128 b状态

ARIA的轮函数由3个部件构成：

1) 混淆层(substitution layer,SL)

选用2个S盒S1和S2以及它们的逆S-11和S-12.每一个S盒定义为F28上的1个可逆的非线性变换函数S：{0,1}8→{0,1}8.ARIA有2种类型的S盒层：

奇数轮采用的变换为

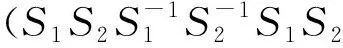
偶数轮采用的变换为

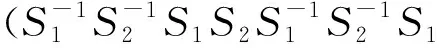
2) 扩散层(diffusion layer,DL)

扩散层是一个{0,1}8×16→{0,1}8×16的映射，为16 B的线性运算：

(y0,y1,…,y15)T=L∘(x0,x1,…,x15)T，

其中，L(x)表示线性函数，“∘”是复合运算符.

其中：

y0=x3⊕x4⊕x6⊕x8⊕x9⊕x13⊕x14，
y1=x2⊕x5⊕x7⊕x8⊕x9⊕x12⊕x15，
y2=x1⊕x4⊕x6⊕x10⊕x11⊕x12⊕x15，
y3=x0⊕x5⊕x7⊕x10⊕x11⊕x13⊕x14，
y4=x0⊕x2⊕x5⊕x8⊕x11⊕x14⊕x15，
y5=x1⊕x3⊕x4⊕x9⊕x10⊕x14⊕x15，
y6=x0⊕x2⊕x7⊕x9⊕x10⊕x12⊕x13，
y7=x1⊕x3⊕x6⊕x8⊕x11⊕x12⊕x13，
y8=x0⊕x1⊕x4⊕x7⊕x10⊕x13⊕x15，
y9=x0⊕x1⊕x5⊕x6⊕x11⊕x12⊕x14，
y10=x2⊕x3⊕x5⊕x6⊕x8⊕x13⊕x15，
y11=x2⊕x3⊕x4⊕x7⊕x9⊕x12⊕x14，
y12=x1⊕x2⊕x6⊕x7⊕x9⊕x11⊕x12，
y13=x0⊕x3⊕x6⊕x7⊕x8⊕x10⊕x13，
y14=x0⊕x3⊕x4⊕x5⊕x9⊕x11⊕x14，
y15=x1⊕x2⊕x4⊕x5⊕x8⊕x10⊕x15.

3) 轮密钥加(round key addition,RKA)

中间状态与128 b的轮子密钥进行异或操作，轮子密钥由密钥编排算法生成.

2 不可能差分攻击

差分密码分析利用高概率特征(或差分)恢复密钥，而不可能差分密码分析方法的基本思想是利用概率为0的特征(或差分)，排除那些导致特征(或差分)概率为0的候选密钥.对于一条概率为0的差分路径，当使用正确密钥解密密文对时，得不到符合该路径的差分；但若使用猜测密钥解密密文对时，得到符合该路径的差分，则该猜测密钥值是错误的；通过这种方法来筛去所有的错误密钥猜测值，那么剩下的就是需要恢复的正确密钥.

利用不可能差分分析对r轮迭代密码进行分析的流程为：

步骤1. 寻找r-1轮差分α0→αr-1，使此特征成立的概率为0.

步骤2. 选择明文对(P,P⊕α0)，满足差分为α0，并进行r轮加密，所得密文记作C和C*.

步骤3. 猜测第r轮轮密钥kr的所有可能值，对每一个猜测密钥分别对C和C*解密1轮，所得到的值记作D和D*；判断D⊕D*=αr-1是否成立，如果成立则对应的猜测值一定是错误密钥.

步骤4. 重复上述步骤，直到密钥唯一确定为止.

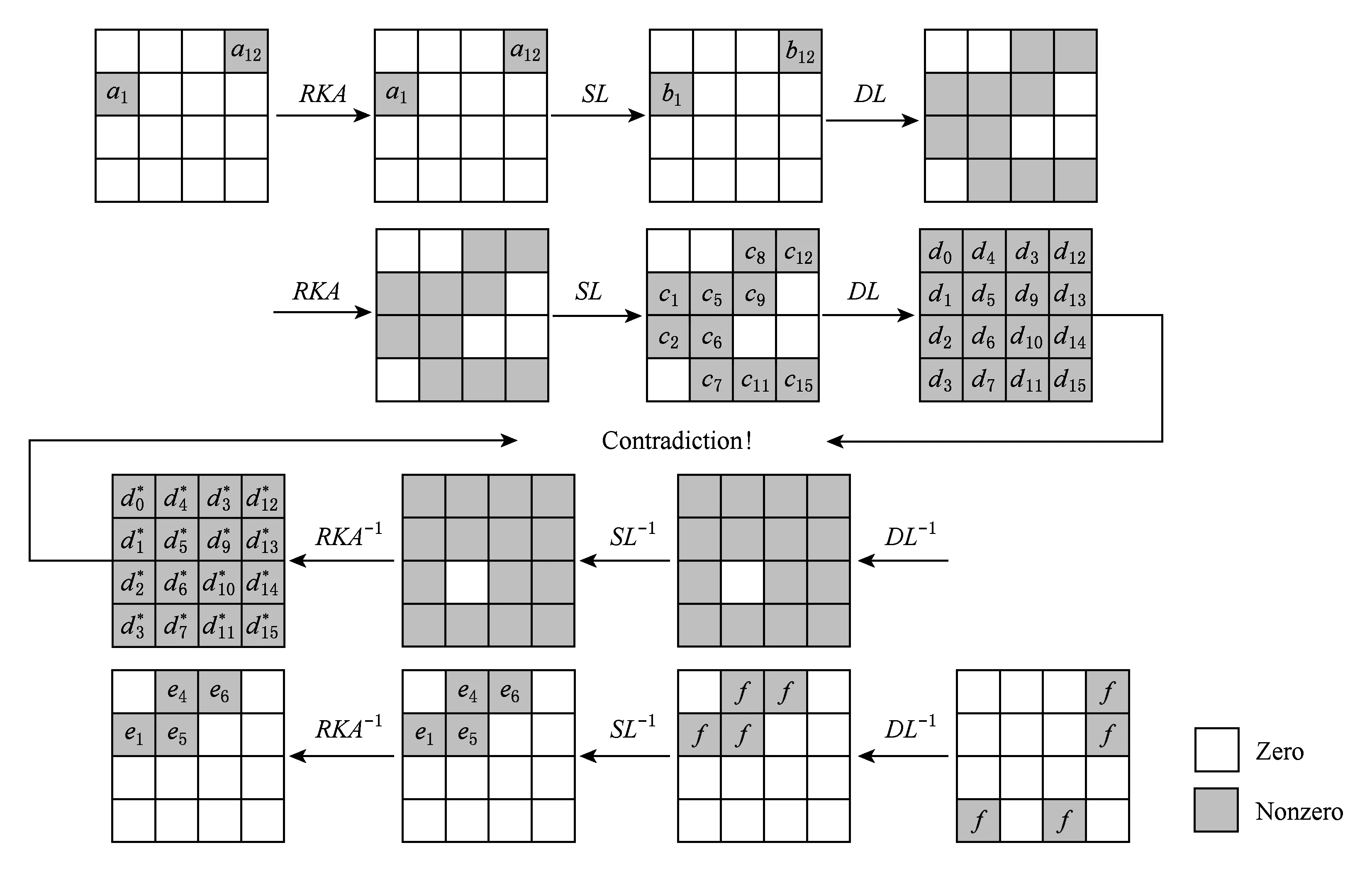
Fig. 2 Features of impossible differential on ARIA图2 ARIA不可能差分性质

假设通过上述攻击可以得到|K|位密钥，每个明密文对可以淘汰2-t的密钥量，为保证正确的密钥被唯一确定，所需要的明密文对N必须满足：

(2|K|-1)×(1-2-t)N<1，

当t比较大时可得：

N>2t×ln 2×|K|≈2t-0.53|K|，

观察此式可以发现，在实现不可能差分密码分析时，所需要猜测的密钥量基本不影响数据复杂度，这便是和其他攻击的不同之处.不可能差分密码分析方法的数据复杂度主要是由每个明密文对所能淘汰密钥的概率所决定的.

3 7轮ARIA算法的不可能差分攻击

本文要构造7轮ARIA密码算法的不可能差分攻击，在新的4轮不可能差分路径的前边增加2轮，后边增加1轮，得到新的7轮不可能差分攻击路径.然后利用ARIA密码算法扩散层的性质，过滤无用的明密文对，大大降低复杂度，构成新的7轮ARIA算法的不可能差分攻击.

3.1 ARIA密码算法的2个性质

性质1. 如图2所示，给定一明文对，满足仅在字节(1,12)处取值不相等，其他字节处相等.在经过4轮变换后，密文对不满足3个性质：

1) 2个密文在字节(3,11,12,13)处不相等；

2) 密文在其他字节处相等；

3) 密文差分在(3,11,12,13)处相等.

即：

(0,a1,0,0,0,0,0,0,0,0,0,0,a12,0,0,0)|→
(0,0,0,f,0,0,0,0,0,0,0,f,f,f,0,0)

是不可能的，其中a1,a12,f是非0值.

证明. ARIA的4轮变换可以分为前2轮变换和后2轮变换这2部分.

对于前2轮变换.假设输入差分为

(0,a1,0,0,0,0,0,0,0,0,0,0,a12,0,0,0)，

因为是用同一密钥对2个明文进行的加密运算，所以经过RKA后差分没有发生变化.

经过SL，差分变为

(0,b1,0,0,0,0,0,0,0,0,0,0,b12,0,0,0)，

其中，b1,b12为非0字节.

随后进行第1轮DL变换，差分变为

p=232264=2-32，

然后进行第2轮RKA和SL变换，差分变为

(0,c1,c2,0,0,c5,c6,c7,c8,c9,0,c11,c12,0,0,c15)，

再进行第2轮的DL变换，差分变为

(d0,d1,…,d15)，

其中，有d6=d11=c2⊕c7⊕c9⊕c12.

至此，完成了ARIA前2轮变换.

再考虑：

(0,0,0,f,0,0,0,0,0,0,0,f,f,f,0,0)

经过2轮变化的逆过程.

经过1次DL-1变换，变成

(0,f,0,0,f,f,0,0,f,0,0,0,0,0,0,0)，

然后再经过1次SL-1变换，差分变为

(0,e1,0,0,e4,e5,0,0,e8,0,0,0,0,0,0,0)，

其中，e1,e4,e5,e8为非0值.

又因为异或子密钥不改变差分值，故直接继续进行下一次DL-1，差分变为

(e4⊕e8,e5⊕e8,e1⊕e4,e5,e5⊕e8,e1⊕e4,
0,e1⊕e8,e1⊕e4,e1⊕e5,e5⊕e8,e4,e1,e8,
e4⊕e5,e1⊕e4⊕e5⊕e8)，

再经过1次SL-1和RKA变换后，差分变为

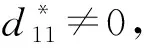
至此，ARIA的2轮逆运算结束.

证毕.

c0=c13=b6⊕b8，

(1)

c3=c14=b5⊕b11，

(2)

c5=c8=b1⊕b15，

(3)

c2⊕c4⊕c7⊕c9⊕c10⊕c15=0.

(4)

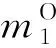
同理可证明式(2)和式(3)都成立.

同时，有：

c2=b1⊕b6⊕b11⊕b15,
c4=b5⊕b8⊕b11⊕b15,
c7=b1⊕b6⊕b8⊕b11,
c9=b1⊕b5⊕b6⊕b11,
c10=b5⊕b6⊕b8⊕b15,
c15=b1⊕b5⊕b8⊕b15.

所以容易得证式(4)也是以概率1成立的.

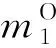
p=248280=2-32.

证毕.

3.2 7轮ARIA的不可能差分攻击过程

本文在3.1节已证明的4轮不可能差分路径的前边增加2轮变换，后边增加1轮变换，得到新的7轮不可能差分攻击，如图3所示.其中ARIA密码算法的最后1轮没有扩散层，取而代之的是轮密钥加(RKA).

攻击过程如下：

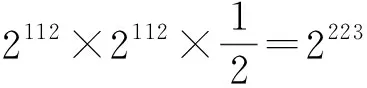
步骤2. 取2N个上述结构(即2N×2223=2223+N个明文对).选取明文对中在(0,1,2,4,5,6,7,8,9,10,14,15)这12 B处差分为0的密文对，满足这样的密文对有2223+N×2-8×(16-4)=2127+N对.

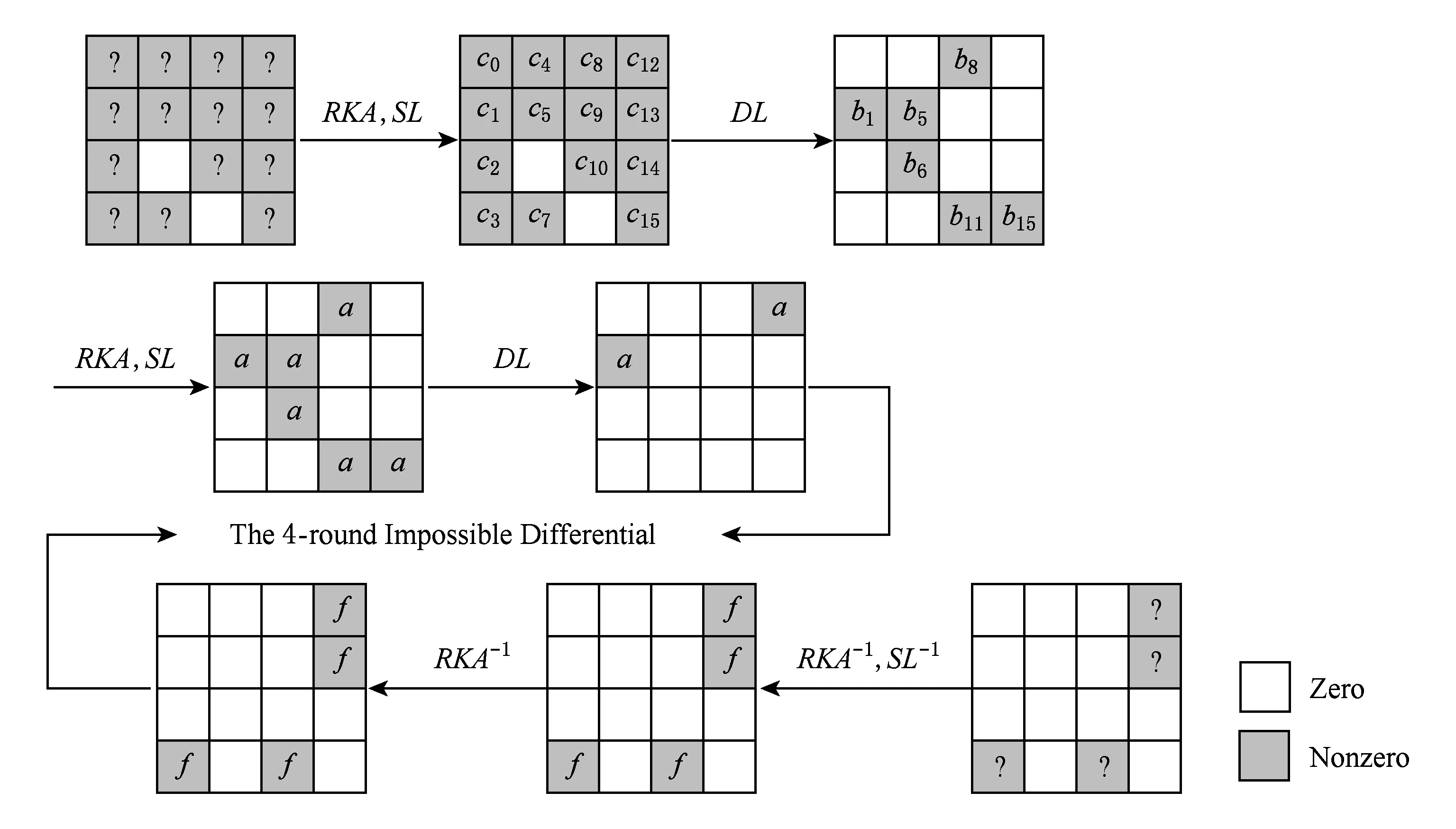
Fig. 3 7-round impossible differential attacks on ARIA图3 7轮ARIA不可能差分攻击

步骤3. 猜测密钥字节(k8,3,k8,11,k8,12,k8,13)，对每个保留下来的密文对(C,C)，分别进行计算：

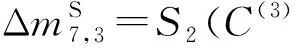
步骤4. 猜测k1的14 B，并利用性质2进行分析.

步骤4.1. 假设剩余的密文所对应的明文对为(P,P)，猜测(k1,0,k1,13)，计算：

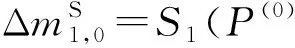
步骤4.2. 猜测(k1,3,k1,14)，计算：

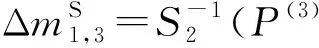
步骤4.3. 类似地，猜测(k1,5,k1,8)密钥字节，计算：

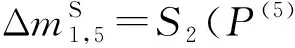
步骤4.4. 猜测(k1,2,k1,4,k1,7,k1,9,k1,10,k1,15)密钥字节，计算：

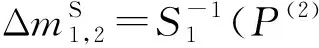
选择满足：

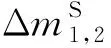
相应明文对.此时剩余的明文对为279+N×2-8=271+N个.

步骤4.5. 猜测(k1,1,k1,12)的值，计算：

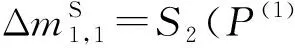
此时没有条件，所以没有过滤.

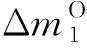
步骤5. 猜测(k2,1,k2,5,k2,6,k2,8,k2,11,k2,15)的值，计算：

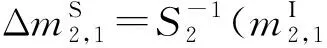
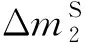
3.3 复杂性分析

分析该攻击的时间复杂度：

在步骤3中，若同时计算4 B的值，时间复杂度为

而实际上，只需3×2149即可.由于可以先对2 B的值进行计算，然后进行比较.如若相等，进行下一步的计算；如若不相等，可直接舍弃，从而达到降低复杂度的效果.对于剩余的对，使用相同的方法进行计算，并和前面的值相比较.如若相等，便保留，如若不相等，则舍弃.同理，对剩余的对，使用相同的方法进一步过滤.此方法称为“early-abort”技术[8].

因为这一步只需要计算4 B的值，所以共需要

次1轮加密运算.

注意到下边的每一步中都有应用“early-abort”技术.

因为在步骤4中，只有RKA和SL这2种运算，故可以认为每一次的运算都相当于23的1轮运算.

所以步骤4中：

步骤4.1需要

次1轮加密；

步骤4.2需要

次1轮加密；

步骤4.3需要

次1轮加密；

步骤4.4需要

次1轮加密；

步骤4.5需要

次1轮加密；

步骤4.6只有DL变换操作，所以需要

次1轮加密.

步骤5需要的复杂度为

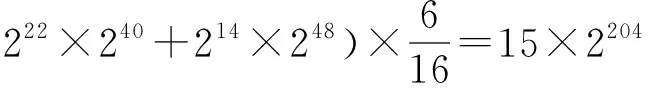
次1轮加密.

所以总的攻击复杂度为

次7轮加密运算.

从分析过程中的步骤1中可知，本文选择明文数为2112，并选择2N个结构，其中N=7，所以本文攻击共需要2119选择明文.

综上，本文的攻击复杂度为：2119选择明文和大约2218次7轮加密运算.

4 8轮ARIA算法的不可能差分攻击

本文要构造8轮ARIA密码算法的不可能差分攻击，类似构造7轮ARIA密码算法的不可能差分攻击，在新的4轮不可能差分路径的前边增加2轮，后边增加2轮，得到新的8轮不可能差分路径.然后利用ARIA密码算法扩散层的性质，过滤掉无用的明密文对，从而构成8轮ARIA算法的不可能差分攻击.

4.1 ARIA密码算法的另一性质

h0=h10=h13=g6⊕g13,

(5)

h2=h9=h12=g11⊕g12,

(6)

h3⊕h4⊕h8=0,

(7)

h1⊕h5⊕h11=0,

(8)

h6⊕h7⊕h14=0.

(9)

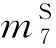
同理可证明式(6)也是成立的.

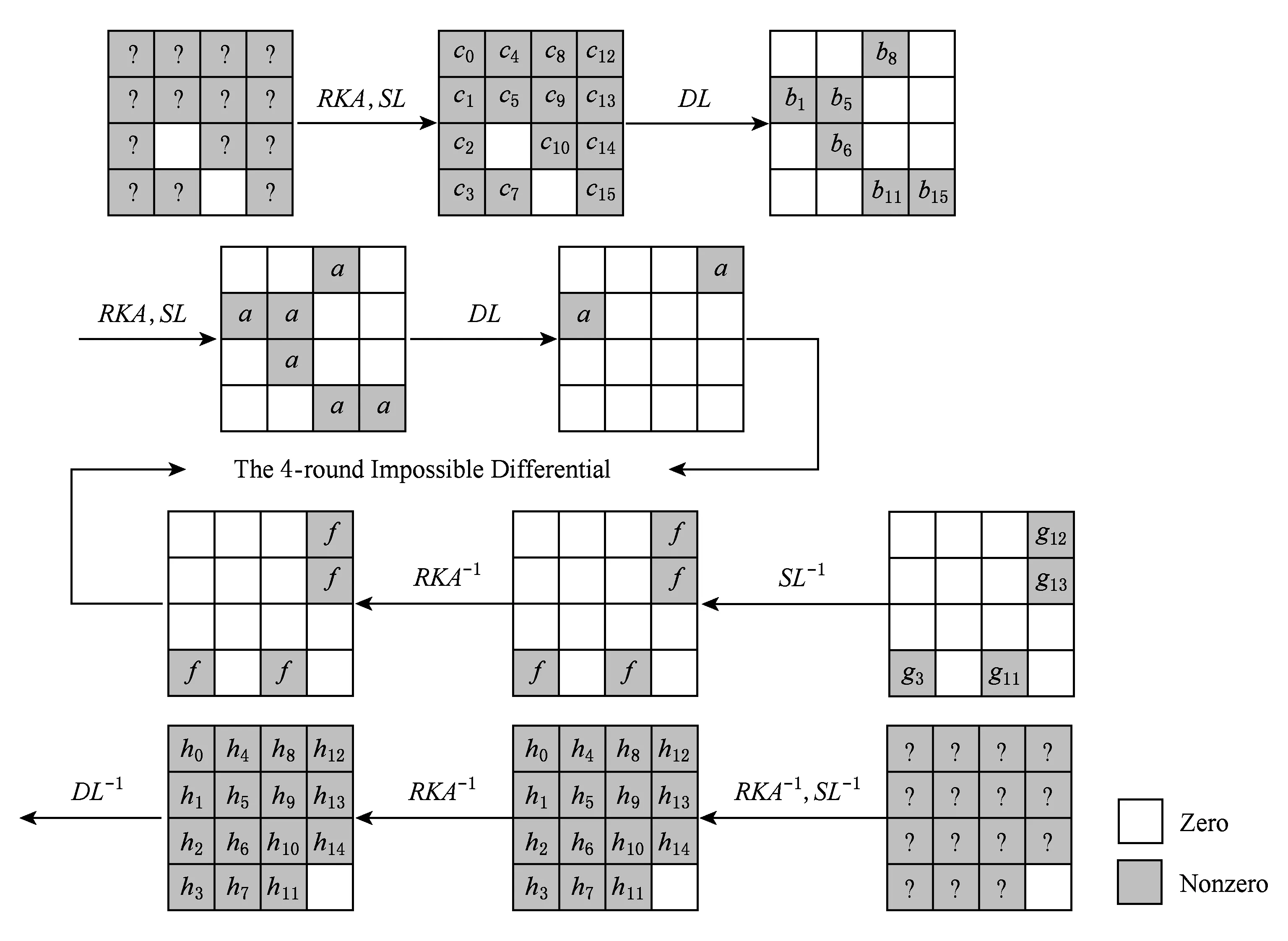
Fig. 4 8-round impossible differential attacks on ARIA图4 8轮ARIA不可能差分攻击

同时，有h3=g11⊕g13，h4=g11，h8=g13.所以容易得证式(7)也是以概率1成立的.同理，h1=g12,h5=g3,h11=g3⊕g12,h6=g12⊕g13,h7=g3⊕g11⊕g12⊕g13,h14=g3⊕g11.所以式(8)和式(9)也是成立的.

证毕.

4.2 8轮ARIA的不可能差分攻击过程

本文在3.1节的性质1已证明4轮不可能差分路径的前边增加2轮，后边增加2轮，得到新的8轮不可能差分攻击，如图4所示.其中ARIA密码算法的最后1轮没有扩散层，取而代之的是轮密钥加(RKA).

攻击过程如下：

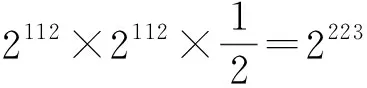
步骤2. 取2N个上述结构(即2N×2223=2223+N个明文对).选取明文对中在第16 B(15)处差分为0的密文对，满足这样的密文对有2223+N×2-8×(16-15)=2215+N对.

步骤3. 猜测密钥字节

(k9,0,k9,1,k9,2,k9,3,k9,4,k9,5,k9,6,k9,7,
k9,8,k9,9,k9,10,k9,11,k9,12,k9,13,k9,14),

对每个保留下来的密文对(C,C)，分别进行如下计算：

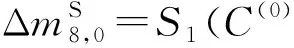
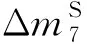
步骤4. 猜测k8的15 B，并利用性质3进行分析.

步骤4.2. 猜测(k8,0,k8,10,k8,13)，并计算：

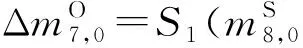
步骤4.3. 猜测(k8,2,k8,9,k8,12)，计算：

步骤4.4. 猜测(k8,3,k8,4,k8,8)密钥字节，计算：

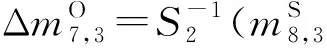
选择满足h3⊕h4⊕h8=0的明文对.剩余的明文对为239+N×2-8=231+N个.

步骤4.5. 猜测(k8,1,k8,5,k8,11)密钥字节，计算：

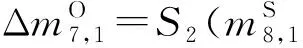
选择满足h1⊕h5⊕h11=0的明文对.剩余的明文对为231+N×2-8=223+N个.

步骤4.6. 猜测(k8,6,k8,7,k8,14)密钥字节，计算：

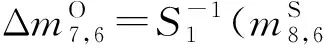
选择满足h6⊕h7⊕h14=0的明文对.剩余的明文对为223+N×2-8=215+N个.

步骤5. 猜测k1的14 B，并利用性质2进行分析.

步骤5.1. 假设剩余的密文所对应的明文对为(P,P)，猜测(k1,0,k1,13)，计算：

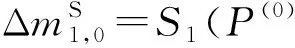
步骤5.2. 猜测(k1,3,k1,14)，计算：

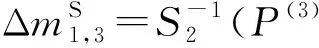
步骤5.3.类似地，猜测(k1,5,k1,8)密钥字节，计算：

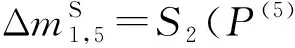
步骤5.4. 猜测(k1,2,k1,4,k1,7,k1,9,k1,10,k1,15)密钥字节，计算：

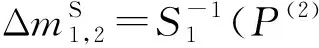
选择满足条件：

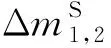
的明文对.此时剩余的明文对为2N-9×2-8=2N-17个.

步骤5.5. 猜测(k1,1,k1,12)的值，计算：

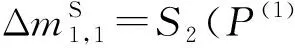
此时没有条件，所以没有过滤.

步骤6. 猜测(k2,1,k2,5,k2,6,k2,8,k2,11,k2,15)的值，计算：

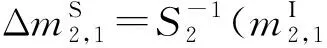
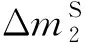
4.3 复杂性分析

分析该攻击的时间复杂度：

在步骤3中，本文依然使用“early-abort”技术，共需要

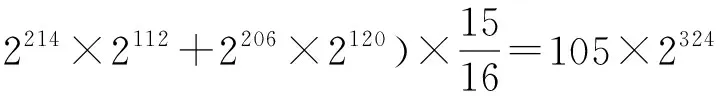
次1轮加密运算.

因为在步骤4中，只有RKA和SL这2种运算，故可以认为每一次的运算都相当于23的1轮运算.

所以步骤4中：

步骤4.1只有DL变换操作，所以需要

次1轮加密；

步骤4.2需要

次1轮加密；

步骤4.3需要

次1轮加密；

步骤4.4需要

次1轮加密；

步骤4.5需要

次1轮加密；

步骤4.6需要

次1轮加密.

在步骤5中，同理，只有RKA和SL运算，可以认为每一次的运算都相当于23的1轮运算.

所以步骤5中：

步骤5.1需要

次1轮加密；

步骤5.2需要

次1轮加密；

步骤5.3需要

次1轮加密；

步骤5.4需要

次1轮加密；

步骤5.5需要

次1轮加密；

步骤5.6只有DL变换操作，所以需要

次1轮加密.

步骤6需要的复杂度为

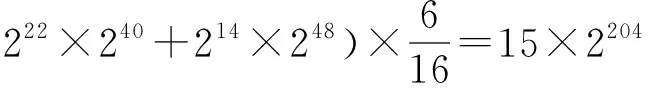
次1轮加密.

所以总的攻击复杂度为

次8轮加密运算.

在分析过程步骤1中，本文选择明文数为2112，并选择2N个结构，其中N=95，所以本文攻击共需要2207选择明文.

综上，本文的攻击复杂度为：2207选择明文和大约2346次8轮加密运算.

5 结 论

本文在证明不可能差分路径成立的基础上，根据ARIA密码的结构特征，在第3节中，于不可能差分路径前面增加2轮、后面增加1轮，实现了对ARIA分组密码算法的新的7轮不可能差分分析.研究表明，此路径下，7轮不可能差分攻击共需要2119选择明文和大约2218次7轮加密运算.与表2中7轮ARIA密码算法的不可能差分攻击结果相比较，攻击进一步降低了数据复杂度和时间复杂度.在第4节，本文首次提出了对ARIA密码算法的8轮不可能差分攻击，在不可能差分路径前面增加2轮、后面增加2轮，构成8轮ARIA密码算法的新攻击.研究表明，在此路径下，8轮ARIA密码算法的不可能差分攻击共需要2207选择明文和大约2346次8轮加密运算.但超过穷举搜索的攻击复杂度，故可认为在该路径下8轮不可能差分攻击中ARIA密码算法是安全的.

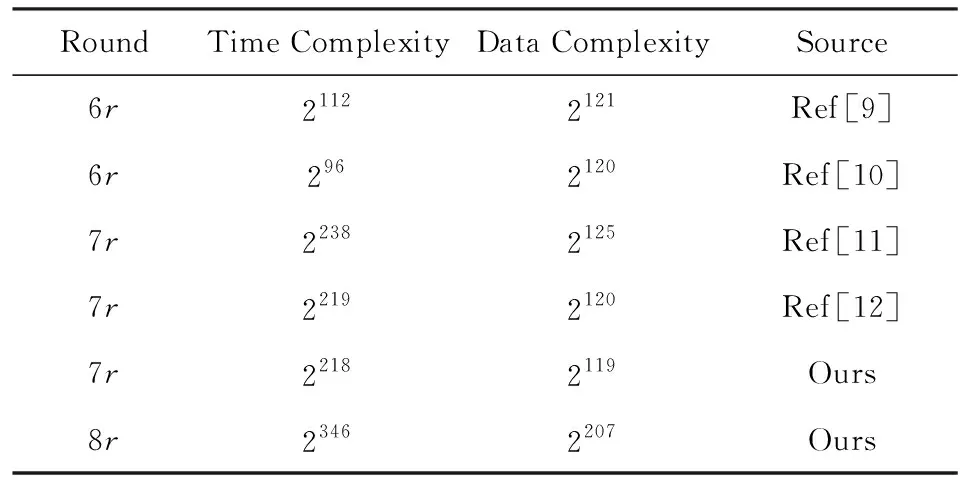
Table 2 Summary of Cryptanalysis of ARIA by ImpossibleDifferential表2 ARIA密码算法的不可能差分分析的安全性总结

在以后的研究中，着重寻找新的不可能差分路径，证明新的不可能差分性质，尝试降低8轮ARIA密码算法不可能差分攻击的时间复杂度和数据复杂度.由于ARIA算法和AES算法结构上相似，很多用来分析AES算法的分析方法对ARIA密码算法肯定具有一定的效果，所以继续对ARIA的其他分析方法进行研究，比如线性攻击、中间相遇攻击、积分攻击等，提高对ARIA算法的攻击轮数.同时，也可以将对ARIA密码算法的分析方法迁移到对AES密码算法的分析中，用来改进AES现有的分析结果.

[1]Daesung K, Jaesung K, Sangwoo P, et al. New block cipher: ARIA[G]LNCS 2971: Proc of the 6th Int Conf on Information Security and Cryptology. Berlin: Springer, 2004: 432-445

[2]Chen Shaozhen. The Basis of Cryptography[M]. Beijing: Science Press, 2008 (in Chinese)(陈少真. 密码学基础[M]. 北京: 科学出版社, 2008)

[3]Stinson D. Cryptography Theory and Practice[M]. Translated by Feng Dengguo. 3rd ed. Beijing: Publishing House of Electronics Industry, 2009 (in Chinese)(Stinson D. 密码学原理与实践[M]. 冯登国, 译. 3版. 北京: 电子工业出版社, 2009)

[4]Liu Ya, Gu Dawu, Liu Zhiqiang, et al. New improved impossible differential attack on reduced-round AES-128[G]LNEE 114: Proc of Computer Science and Convergence. Berlin: Springer, 2012: 453-461

[5]Mala H, Dakhilalian M, Rijmen V, et al. Improved impossible differential cryptanalysis of 7-round AES-128[G]LNCS 6498: Proc of the 11th Int Conf on Cryptology in India. Berlin: Springer, 2010: 282-291

[6]Dunkelman O. Techniques for cryptanalysis of block ciphers[D]. Haifa, Israel: Technion-Israel Institute of Technology, Faculty of Computer Science, 2006

[7]Biryukov A, Wagner D. Slide attacks[G]LNCS 1636: Proc of the 6th Int Workshop on Fast Software Encryption. Berlin: Springer, 1999: 245-259

[8]Du Chenghang. Impossible differential analysis and middle encounter attack of block cipher algorithm ARIA[D]. Jinan: Shandong University, 2011 (in Chinese)(杜承航. 分组密码算法ARIA的不可能差分分析和中间相遇攻击[D]. 济南: 山东大学, 2011)

[9]Wu Wenling, Zhang Wentao, Feng Dengguo. Impossible differential cryptanalysis of reduced-round ARIA and Camellia[J]. Journal of Computer Science and Technology, 2007, 22(3): 449-456

[10]Li Shenhua, Song Chunyan. Improved impossible differential cryptanalysis of ARIA[C]Proc of the 2008 Int Conf on Information Security and Assurance. Los Alamitos, CA: IEEE Computer Society, 2008: 129-132

[11]Du Chenghang, Chen Jiezhe. Impossible differential cryptanalysis of ARIA reduced to 7 rounds[G]LNCS 6467: Proc of the 9th Int Conf on Cryptology and Network Security. Berlin: Springer, 2010: 20-30

[12]Su Chongmao. New impossible differential attack on 7-round reduced ARIA[J]. Journal of Computer Applications, 2012, 32(1): 45-48 (in Chinese)(苏崇茂. 7轮ARIA-256的不可能差分新攻击[J]. 计算机应用, 2012, 32(1): 45-48)

XieGaoqi, born in 1994. Master. His main research interests include cryptanalysis of block ciphers.

WeiHongru, born in 1963. Associate professor. His main research interests include mathematics, information security and cryptography, and key technologies of Internet of things.