标准环+转弯环的双面楔形盾构管片排版技术研究

刘 欣， 刘 鑫， 柳宪东

(广州地铁设计研究院有限公司， 广东 广州 510010)

0 引言

伴随着地下空间工程的迅猛发展，盾构法成为隧道建设的主流方法，其在建筑物密集、管线繁多和施工影响限制严苛的城市中具有明显的优势。盾构在掘进前，需要对隧道进行预排版选型以便确定工程量，并提前预制所需数量和类型的管片； 在掘进过程中，还需根据现场实际情况不断对下一环管片的排版选型进行调整。在实际工程中，施工人员往往根据设计图纸及实测管片安装误差，通过手工计算或直接凭经验判断后续管片排版选型的方案，增加了施工误差和错误的风险，降低了施工效率和准确度。同时，施工人员对于手工计算或经验判断的结果缺乏直观的效果评估，不利于施工人员之间的沟通。因此，对管片排版方法进行理论研究可以较为精确地统计工程所需管片的数量和类型，可以对隧道掘进路线进行预判，还可以跟踪施工进度，对施工的实施拼装监测数据进行分析判断，同时，可对后续管片拼装进行实时纠偏设计，实现设计对施工质量的实时干预和控制。

目前，国内文献关于管片类型的研究主要集中在通用环的排版计算方法方面。刘凤华[1]通过对管片的几何关系进行分析，推导了通用环管片的排版公式，并探讨了盾尾间隙及油缸行程差对盾构管片拼装的影响。潘国荣等[2]通过分析设计轴线、盾构推进既成轴线和管片成型轴线之间的关系，提出了一种通用型管片的纠偏方法。储柯钧[3]根据设计线路的曲线要素特点及管片楔形量计算出在不同半径的曲线上所需标准环与楔形环的配比，虽然提到了标准环与楔形环的组合拼装，但并未对管片选型及拼装姿态进行具体分析。张志华等[4]在每环管片内建立局部坐标系，以局部坐标系描述管片拼装信息，并以通用管片为例进行了验证。张文萃等[5]以宁波地铁2号线为例，计算了通用管片在不同点位拼装时各方向的超差和轴线偏差，分析了通用管片排版设计时应当考虑的影响因素。张忠桢等[6]根据双面楔形管片是等腰楔形环这一几何特性，利用齐次变换方法计算出每环管片的位置和方位，进而确定盾构线路所需左、右转弯环的数量。

广州、南京和长沙等城市地铁建设的盾构隧道均采用了标准环+转弯环组合的管片，而目前国内关于标准环+转弯环排版方法的研究较少。为此，本文针对管片类型为标准环+转弯环(为双面楔形)组合的盾构隧道，提出了一种错缝拼装形式的管片预排版方法。

1 基本思路

假设管片尺寸参数外径为D，中心环宽为B，楔形量为Δ，单位轴转角γ= 360°/N(N为环间螺栓组数量)。

在盾构掘进过程中，目标设计线路为三维曲线，计算时需要选择合适的管片类型和旋转角度，取得最接近目标线路的一种拼装姿态。通过分析可知，3类管片共存在3N种拼装模式。首先，对分析过程做以下3点限制，尽可能排除不需要计算的管片姿态以减少运算量，设封顶块与管片沿掘进方向水平面左向(管片圆心9点方向)的夹角为θ，则：

1)封顶块需要在管片上半圆范围内，即以水平面与管片左半圆交点为起点的0°～180°内，θ∈[0°,180°]；

2)避免通缝拼装，拼装环与当前环管片的拼装点位不可相同；

3)若拼装环为标准环，当θ<180°时，则标准环强制旋转角度为(θ+γ)，当θ≥180°时，则强制旋转角度为(θ-γ)。

综合以上分析，通过计算可得管片拼装模式为(N-2)种。

2环盾构管片的拼装姿态几何图如图1所示。由管片的几何参数可知： tanα= 2D/Δ。根据已拼装情况，还可知以下参量：

1)当前环管片类型(标准环或左右转弯环)；

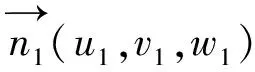
3)当前环封顶块与管片圆心9点方向的夹角θ0；

4)当前线路方程f(L)及里程L0。

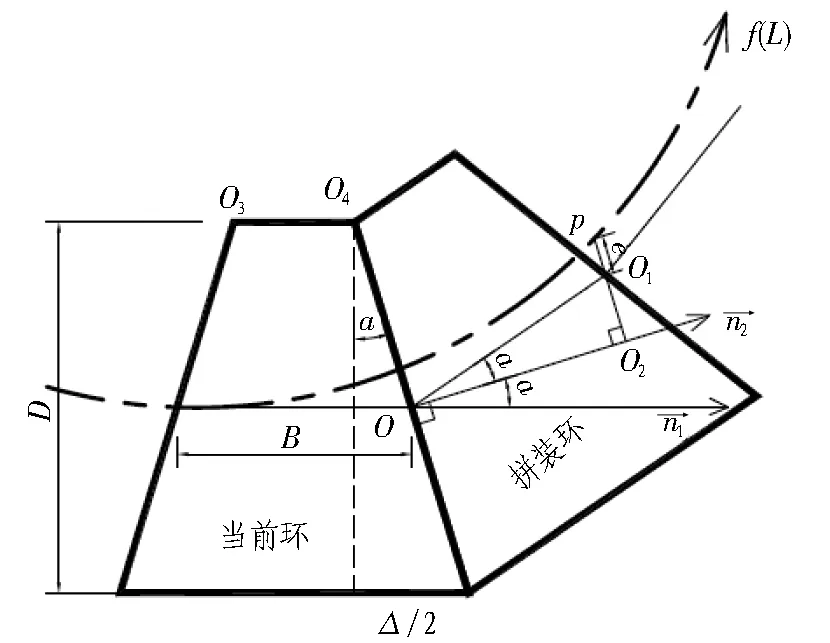
图1 管片拼装姿态几何分析图

计算比较拼装环在管片类型和旋转角度不同时与目标线路的误差，即图1中点p与点O1的距离e，选出误差最小的拼装姿势作为最优解。

2 几何方程

(1)

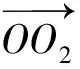
(2)

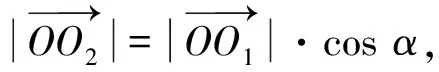
(3)

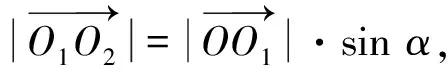
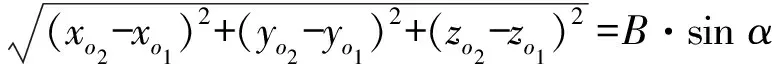
(4)

设当前环终点面最大楔形量剖面短边角点为O4，则有如下关系：

(5)

由公式(5)可求得O4坐标(xo4,yo4,zo4)。

由三角关系得：

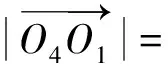
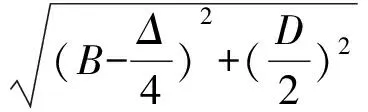
(6)

设管片计算轴转角顺时针旋转为正，拼装环相对当前环的转动角度β=N·γ，管片点位旋转示意图如图2所示，则有：

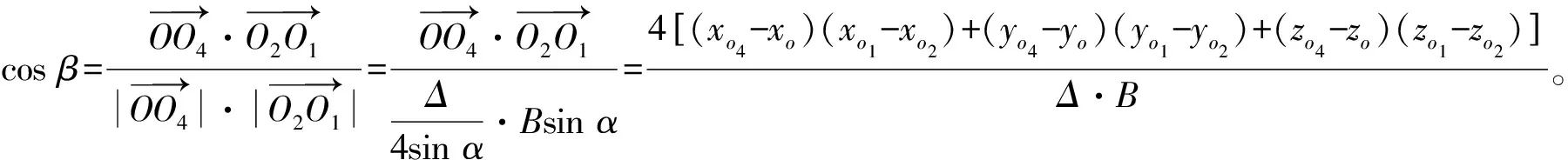
(7)

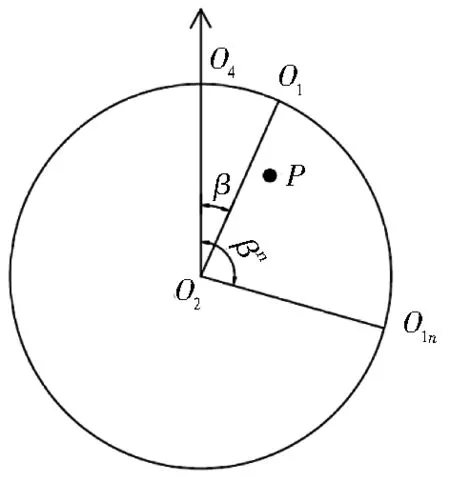
图2 管片点位旋转示意图Fig. 2 Sketch of shield segment point rotation

通过分析可知，未知数为O1坐标(xo1,yo1,zo1)和O2坐标(xo2,yo2,zo2)，方程组为式(1)—(4)、(6)及(7)。未知数数量与互不线性相关的关系式数量相同，方程组可解，结合第1节所述限制条件，可得到(N-2)种解，即(N-2)种拼装环的管片姿态。

(8)

初始迭代点P0坐标取f(L1=L0+B)，d<限值，取此时P点的坐标； 反之，取Pn坐标为f(Ln-1-d)继续计算，直到d<限值，以所求Pn坐标作为交点P的坐标(xp,yp,zp)。

分别求出点O1n与点P的距离，见式(9)，取得最小值时便是拼装环管片姿态的最优解。

(9)

(10)

此时，θ1=θ0+β(θ1>360°时，θ1=θ1-360)。根据线路确定了拼装环的姿态后，拼装环便成为当前环，继续计算下一拼装环管片的姿态。

3 工程实例分析

以南京地铁3号线某区间右线为例对管片拼装的计算方法进行验证。该区间为盾构区间，盾构管片外径为6 200 mm，管片厚度为350 mm，管片宽度为1 200 mm。工程中采用标准环+左、右转弯环拼装方式，转弯环为双面楔形环管片，楔形量为37.2 mm。单面楔角为10′18.79″，环间共设16组螺栓，则单位轴转角为γ=360°/16=22.5°。每环管片由3块标准块、2块邻接块以及1块封顶块组成。盾构管片分块图如图3所示。最大楔形量短边角点在拱腰处，左转弯环封顶块的螺栓组位于最大楔量短边角点的3γ=67.5°处，右转弯环封顶块的螺栓组位于最大楔形量短边角点的-3γ=-67.5°处。

隧道设计轴线两端为直线，中间曲线中缓和曲线长70 m，圆曲线半径450 m，切线长107.318 m。竖曲线交点里程为YDK28+013，标高为1.758 m，后视坡度为2.55%，前视坡度为-0.494 3%。

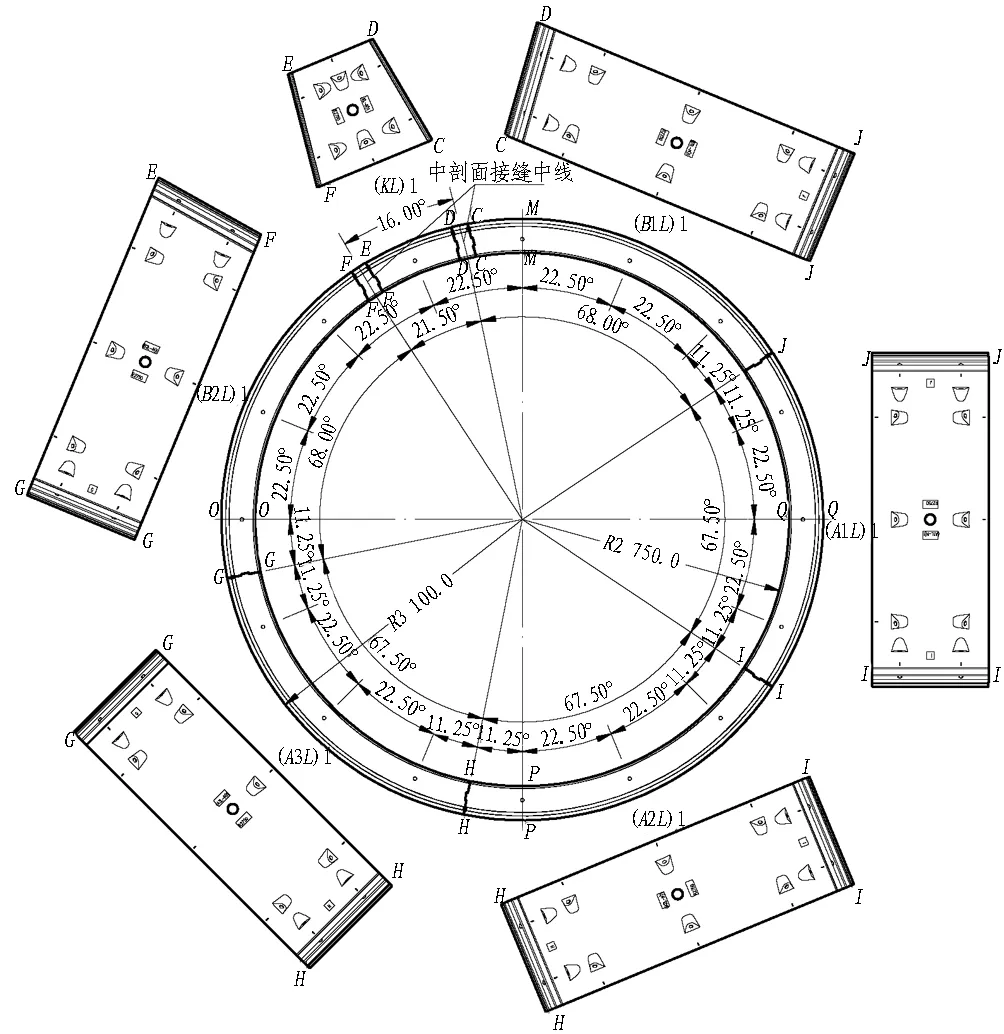
图3 盾构管片分块图(单位： mm)Fig. 3 Sketch of shield segment blocks (unit: mm)

通过计算排版，得出右线管片拼装结果见表1。利用Auto revit软件建模，拼装效果如图4所示。

表1南京地铁3号线某区间右线管片拼装计算结果

Table 1 Layout calculation results of segments of a right line shield tunnel on Nanjing Metro Line 3

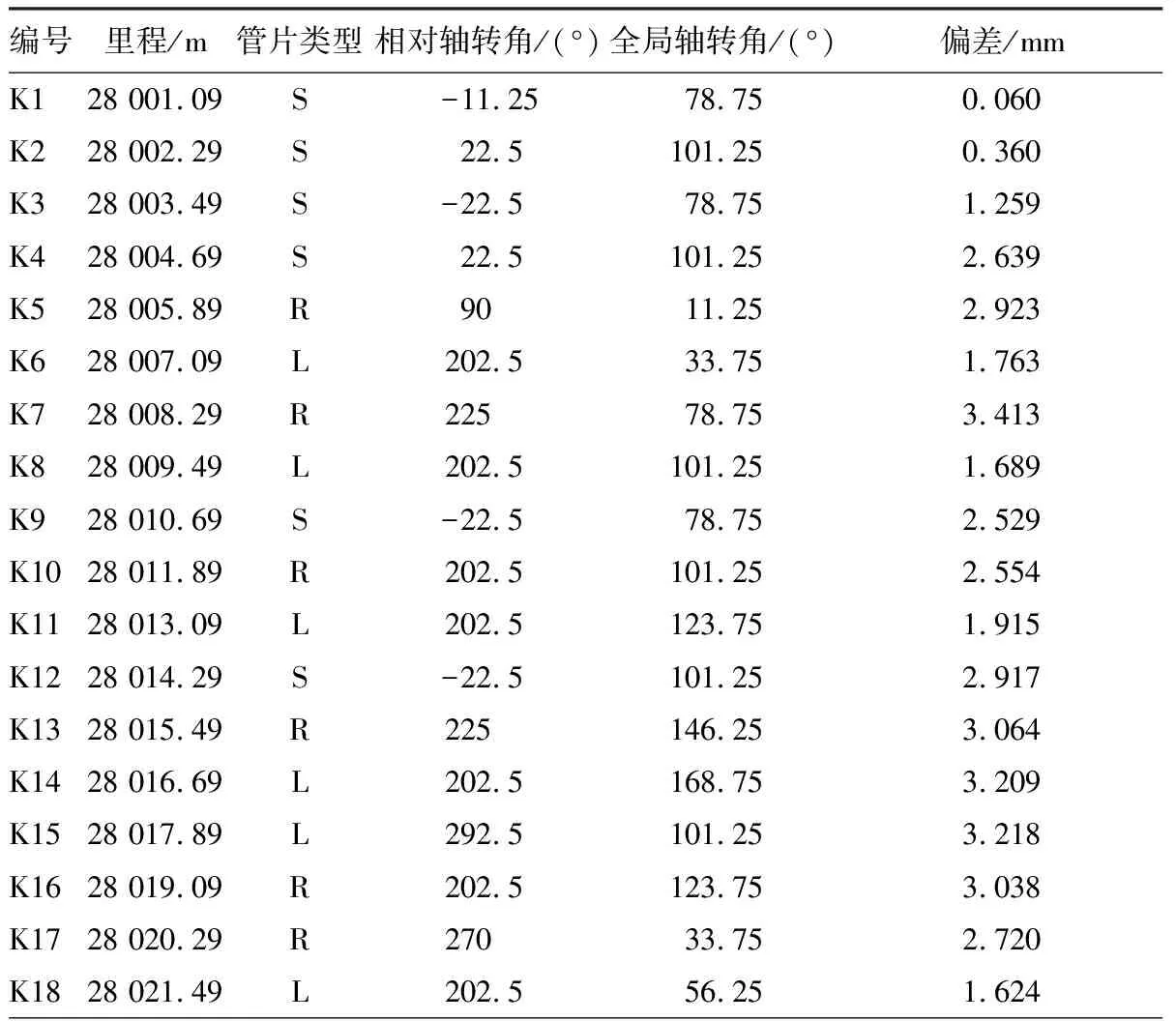
编号里程/m管片类型相对轴转角/(°)全局轴转角/(°)偏差/mmK128 001.09S-11.2578.750.060K228 002.29S22.5101.250.360K328 003.49S-22.578.751.259K428 004.69S22.5101.252.639K528 005.89R9011.252.923K628 007.09L202.533.751.763K728 008.29R22578.753.413K828 009.49L202.5101.251.689K928 010.69S-22.578.752.529K1028 011.89R202.5101.252.554K1128 013.09L202.5123.751.915K1228 014.29S-22.5101.252.917K1328 015.49R225146.253.064K1428 016.69L202.5168.753.209K1528 017.89L292.5101.253.218K1628 019.09R202.5123.753.038K1728 020.29R27033.752.720K1828 021.49L202.556.251.624

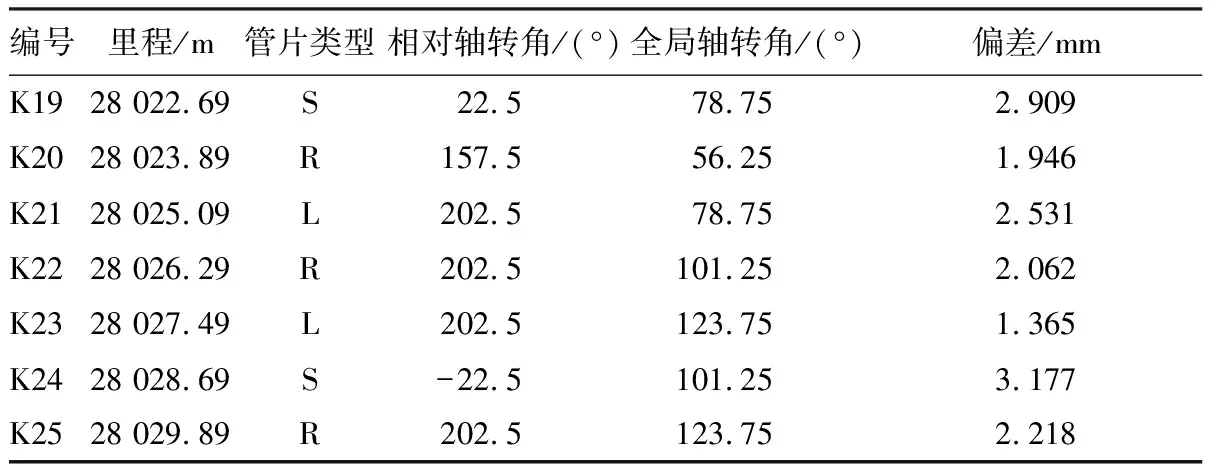
表1(续)

图4 盾构管片拼装效果图Fig. 4 Layout effect of shield segments

由表1可以看出，在线路转弯时，最佳配置并不只是单纯标准环与一种转弯环的组合，其他组合与理论线路的误差也保持在3.3 mm以下。根据此方法排版施工，只要保证施工质量，完全可满足《盾构法隧道施工与验收规范》[7]中要求盾构拼装在平面与高程上的±50 mm的误差。

4 结论与讨论

本文通过分析盾构管片的几何特点，提出了一种错缝拼装、标准环+转弯环(为双面楔形)组合的盾构管片预排版方法，具体介绍了从管片选型、拼装姿态确定到拼装误差计算的分析过程，并以南京3号线区间为例，验证了计算方法的准确性，得到以下结论：

1)在盾构管片错缝拼装方式下，根据管片分块情况和封顶块位于管片上半圆的施工要求，以及对标准环选择角度的限制，将计算单环管片的拼装类型由3N种(N为环间螺栓组数量)优化为(N-2)种，大大提高了运算效率。

2)在求得(N-2)种拼装环的管片姿态后，采用显式迭代法获取目标线路与拼装环旋转面的交点，进而筛选出最优的拼装点位，减少了方程组的未知数数量，增加了求解方程的便捷性和可行性。

3)通过对实际工程案例的计算和建模分析，本文提出的计算方法与目标线路的偏差在毫米级，计算精度得到了有力的验证。

综上可知，该方法降低了管片排版错误的可能性，减轻了施工人员的工作量，对盾构隧道掘进的施工组织和施工误差控制具有重要意义。针对该方法，也提出了以下讨论与建议：

1)在确定每环管片拼装姿势时，均需要求解六元方程组(N-2)次，虽然在计算机内可以快速执行，但1条线路一般有十几km甚至几十km的盾构隧道长度，计算时长是一个需要考虑的问题。

2)制定更简便的拼装方式，将会有效减少运算量。计算前每排除一种拼装模式，确定1环管片拼装姿态时将减少1次求解方程组，对于大规模计算来说，能在一定程度上缩短运算时间。

3)该方法只适用于错缝拼装的标准环与转弯环组合的盾构隧道，并不适用于采用通缝拼装或通用管片环的盾构隧道。

参考文献(References)：

[1] 刘凤华. 盾构隧道通用管片拟合排版与管片选型技术研究[D]. 上海： 同济大学, 2007.

LIU Fenghua. Study of composition and ring selection technology of universal segments for shield-driven tunnels[D]. Shanghai: Tongji University, 2007.

[2] 潘国荣, 荣一夫. 盾构通用管片排版与纠偏控制的简化解算[J]. 大地测量与地球动力学, 2014, 34(1): 55.

PAN Guorong, RONG Yifu. Simplified calculation of gemeral segment composition and correction control[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 55.

[3] 储柯钧. 地铁盾构管片在平、竖曲线上的排版探讨[J]. 隧道建设, 2007, 27(4): 20.

CHU Kejun. Array of segment rings for shield-driven metro tunnel[J]. Tunnel Construction, 2007, 27(4): 20.

[4] 张志华, 朱国力, 隆泗. 盾构管片排版计算方法的研究[J]. 地下空间与工程学报, 2013, 9(5): 1040.

ZHANG Zhihua, ZHU Guoli, LONG Si. Study of calculating method for composition of segments for shield tunnels[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(5): 1040.

[5] 张文萃, 穆世旭, 李家涛, 等. 盾构隧道通用管片排版设计与纠偏研究[J]. 施工技术, 2013, 42(13): 89.

ZHANG Wencui, MU Shixu, LI Jiatao, et al. Research on layout design and deviation correction of the general segment in shield tunnels[J]. Construction Technology, 2013, 42(13): 89.

[6] 张忠桢, 骆汉宾, 余群舟, 等. 地铁圆弧形隧道等腰楔形环的拼装与设计—齐次变换方法[J]. 隧道建设, 2017, 37(10): 1217.

ZHANG Zhongzhen, LUO Hanbin, YU Qunzhou, et al. Design and assembly of isosceles wedged rings for circular metro shield tunnel: A homogeneous transformation method[J]. Tunnel Construction, 2017, 37(10): 1217.

[7] 盾构法隧道施工与验收规范: GB 50446—2008[S]. 北京: 中国建筑工业出版社, 2008.

Code for construction and acceptance of shield tunneling method： GB 50446-2008[S]. Beijing: China Architecture & Building Press, 2008.