砂卵石层矩形顶管机切削技术及排渣系统研究与应用

狄晓红

(中铁工程装备集团有限公司， 河南 郑州 450016)

0 引言

矩形顶管机是一种矩形隧道暗挖施工装备，其工作原理是在盾体系统的保护下，通过开挖系统切削岩土，切削下来的渣土通过排渣系统排出隧道，通过工作井口的起重设备将衬砌管节安放到位，再利用工作井内顶推系统推动顶管机和管节前进，实现隧道开挖和衬砌管节的铺设施工，直至隧道成型。矩形顶管机相比圆形掘进机，大大提高了开挖断面空间利用率，能够有效适应城市浅覆土、狭窄空间隧道施工，已逐步应用于地铁出入口、过街通道、综合管廊和地下停车库等领域[1-3]。但目前国内外制造的矩形顶管机适用的地层相对单一，主要适用于淤泥、黏土、粉土以及沙土等软土地层[4-5]。

富水砂卵石地层在力学机制上表现出强烈的不稳定性，主要特征呈现为岩体松散、无胶结、自稳能力差、围岩整体强度较低，但单个岩块强度较高[6-8]。矩形顶管机在卵石层中掘进存在的主要问题表现为： 1)软土地层前后刀盘布置存在卡卵石现象，极易造成刀盘、驱动冲击损害； 开挖后的大量卵石又会积聚在矩形开挖断面底部，使顶管机底部刀盘旋转阻力大幅增加，导致刀盘驱动超载而经常跳停。2)不同于软土地层，采取降水措施后的砂卵石渣土流动性差，仅靠土舱压力渣土难以直接进入螺旋输送机，影响了渣土的顺利排出，给螺旋输送机结构设计带来挑战； 此外，砂卵石层出渣时在螺旋输送机常规插板式闸门位置容易产生积渣，造成闸门不能完全关闭，稀浆易外漏，严重影响主机内部施工环境。针对富水砂卵石地层矩形顶管机施工，仅有范磊[9]有所研究，其对同平面刀盘的结构和刀具布置以及带式双螺旋输送机结构进行了初步探索，并取得了一定效果，但并未涉及切削系统选型及其减阻设计。本文依托成都下穿人民南路人行通道工程，针对砂卵石地层的特点，采用计算机仿真及工程试验分析等方法，对上述问题及该设备在工程应用中提高螺旋输送机出渣效果的措施进行深入探究，以期为矩形顶管的设计及其穿越砂卵石地层施工提供参考。

1 依托工程概况

该砂卵石地层矩形顶管机依托成都市下穿人民南路人行通道项目进行工程试验，项目位于成都市人民南路三段、华西第四医院正门南侧约20 m处。隧道顶管段长为56 m，埋深为4.8 m，施工断面为6.02 m×4.52 m。顶部垂直方向有约15条各类市政管线，距最近的1条管线仅0.5 m，并垂直上跨正在运营的地铁1号线，距地铁隧道顶板仅3.1 m，如图1所示。

图1 下穿人民南路人行通道效果图(单位： m)

根据工程地勘资料，矩形顶管机穿越的地层以中密卵石为主，局部夹杂中砂、稍密卵石、密实卵石，地下水静止水位埋深为4～5 m。卵石含量为60%～70%，粒径以4～10 cm为主，填充物为细砂、圆砾及局部漂石(项目实际施工中漂石直径达到400 mm)，砾石强度可达30～80 MPa。

2 砂卵石层矩形开挖系统研究

2.1 砂卵石层矩形开挖形式分析

通常矩形断面顶管开挖系统多采用仿形摆动刀盘形式或平行轴多刀盘组合形式。针对稳定性差的富水砂、卵石地层，且又是在浅覆土中，对地层扰动相对较大的摆动刀盘[10]开挖形式显然不适应。平行轴多刀盘组合开挖形式包括刀盘前后平面布置形式和同平面布置形式[3]，针对砂卵石地层，2种刀盘形式是否均能适用尚无案例可循，本文将对此进行针对性的分析。

2.1.1 卵石对前后布置的刀盘冲击影响分析

平行轴前后平面布置时，针对该工程断面，开挖系统采用常规软土辐条式刀盘布置，以开挖盲区最小、刀盘搅拌最为充分为优化目标。经对刀盘布置模拟，初步采用6个平行轴φ2 450 mm的圆刀盘三前三后布置，前刀盘后面板至后刀盘前面板间距采用常规设计中的115 mm(其中切刀刀高选为90 mm)，前后刀盘布置如图2所示。

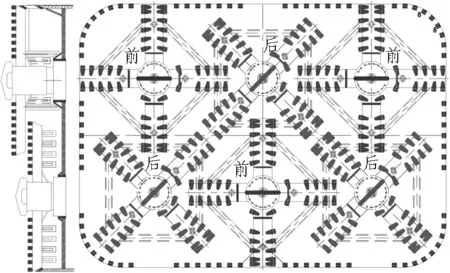
图2 前后刀盘布置

砂卵石地层中常会出现一些较大的卵石，刀盘前后布置需考虑卵石卡刀盘问题，避免冲击对刀盘或驱动系统造成损坏。针对上述问题，建立了刀盘前后布置卵石冲击破碎模型，如图3和图4所示。

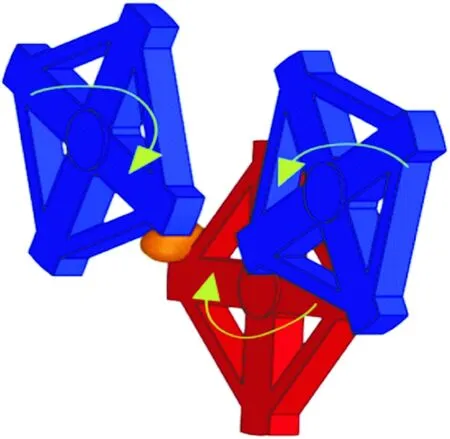
图3 前后刀盘布置模型

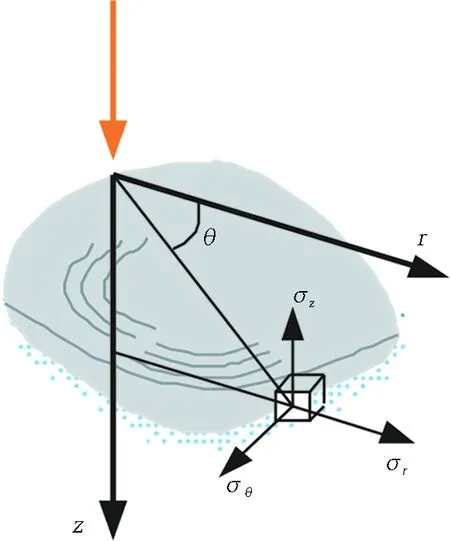
图4 卵石冲击下单元体应力状态模型

基于岩石冲击破碎理论[9]，以卵石与后刀盘撞击时的接触点为圆柱坐标中心，以卵石与前刀盘的接触点为目标单元体进行受力分析，得出3个方向的应力分量：

(1)

式中：Pz为刀盘冲击力；μ为泊松比；R、z、r为圆柱坐标。

当卵石达到破碎临界点时，即当轴向应力σz>σucs(σucs为卵石抗压强度极限)，岩石将整体破碎。将σz=σucs带入式(1)即可求出岩石破碎时的冲击力。

将上述冲击载荷作为有限元分析的边界条件，将刀盘卵石冲击三维模型导入ANSYS中。添加模型材料属性，刀盘体材料选择为Q345B，刀盘的承受极限为230 MPa(许用应力)，对刀盘卵石接触面施加80 MPa的卵石冲击载荷，约束刀盘筒体，进行刀盘受载仿真分析，结果如图5所示。

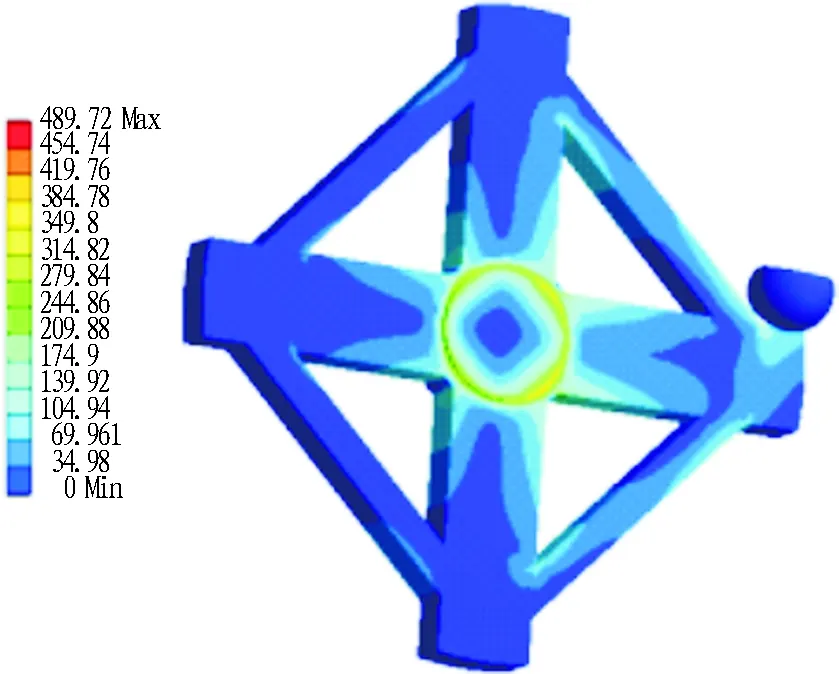
(a) 应力云图(单位： MPa)

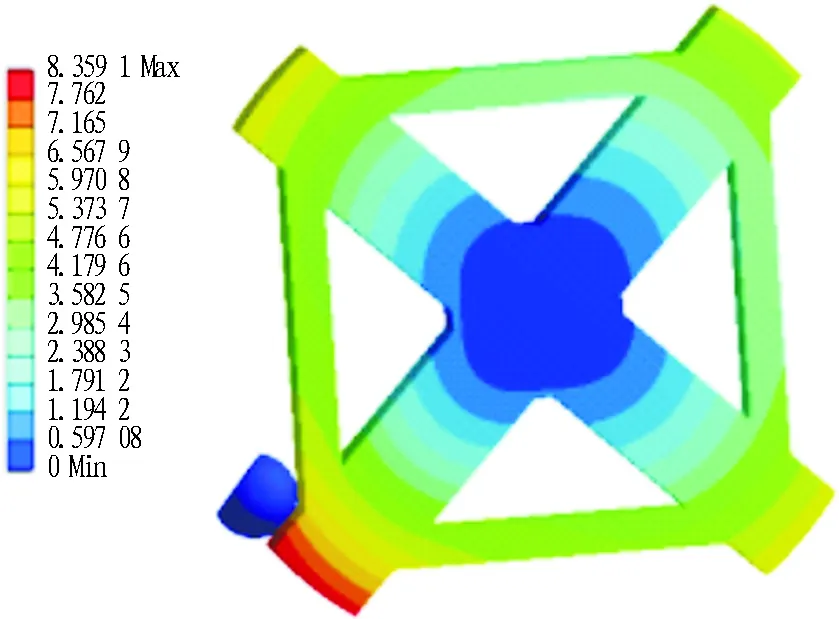
(b) 变形云图(单位： mm)

Fig. 5 Finite element analysis of cutterhead under load of cobble impact

从图5可以看出： 刀盘前后布置运转中遇到卵石冲击时，刀盘最大变形达到8.359 1 mm，最大应力接近500 MPa，已大大超出刀盘的承受极限，也就是说刀盘前后布置存在极大的施工风险，因此在砂卵石地层中不建议采用前后刀盘布置形式。

2.1.2 刀盘同平面布置分析

平行轴同平面刀盘布置同样以开挖盲区最小为设计目标。如图6所示，刀盘布置采用了大(φ2 200 mm 4个)、中(φ1 630 mm 2个)、小(φ1 200 mm 2个)多直径大小刀盘同平面组合布置形式，具体刀盘结构、刀具布置设计见文献[9]。同平面刀盘掘进受载较为简单，刀盘承受的轴向推力为前方土体传递过来的土压力，刀盘承受最大转矩为主驱动额定转矩。对各刀盘进行有限元仿真分析，在最大边界条件作用下，各刀盘的强度和刚度均满足要求[11]。

刀盘同平面布置不存在前后刀盘卡卵石的情况，但2个刀盘反向旋转时对卵石存在类似轧制的作用效果，也可能存在卡刀盘风险。对此，构建同平面刀盘咬石破岩模型，如图7所示，卵石与刀盘接触瞬间刀盘对卵石作用时，刀盘对卵石的径向压力为P，还有对卵石的切向摩擦力F，二者互相垂直。当把P、F分别分解于x轴、y轴方向，可得4个分力Px、Py、Fx、Fy。

由轧制理论可知，卵石咬入条件为Fy>Py，转化易得卵石咬入条件为β(摩擦角)>γ(咬入角)。

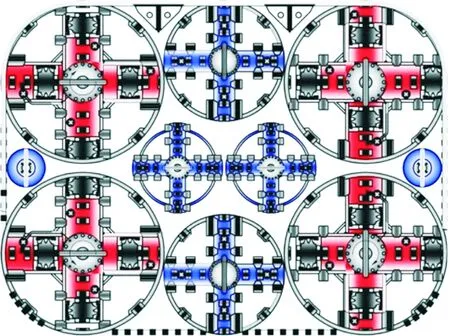
图6 同平面刀盘布置图

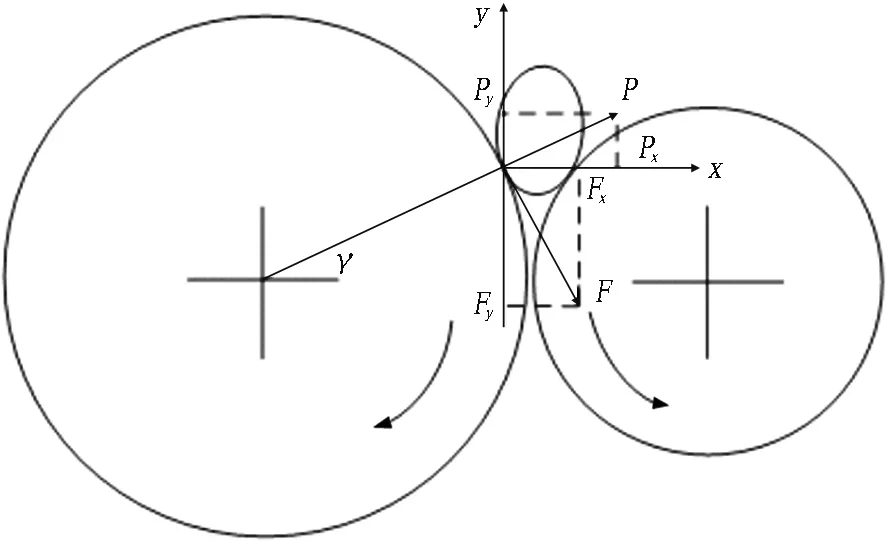
图7 同平面刀盘咬石破岩模型

金属间的静摩擦因数f为0.3～0.4，令f取最大值0.4，而摩擦因数与摩擦角满足f=tanβ，可计算岩石最大咬入角为21.8°，以φ2 200 mm和φ1 630 mm两相邻刀盘为例(左下两刀盘)，卵石被咬入的条件为同时进入两刀盘的咬入角内，容易求得能被咬入的最大卵石尺寸为117 mm，即较大尺寸卵石(>117 mm)不会被刀盘咬入造成较大冲击。将80 MPa小尺寸卵石的破碎冲击力作为边界条件，施加于刀盘大圆环辐条之间的中间最薄弱位置，约束刀盘筒体，对φ1 630 mm刀盘模型进行有限元分析，结果如图8所示。

由图8可以看出： 刀盘同平面布置反向旋转咬入卵石时，刀盘最大变形为0.4 mm，最大应力为101.57 MPa，均在刀盘的许用强度和刚度范围内，即较大卵石不会被两相邻刀盘咬入破碎，较小卵石咬入后可被刀盘直接破碎。综上，矩形顶管机在砂卵石层的开挖系统应采用同平面多刀盘布置形式。

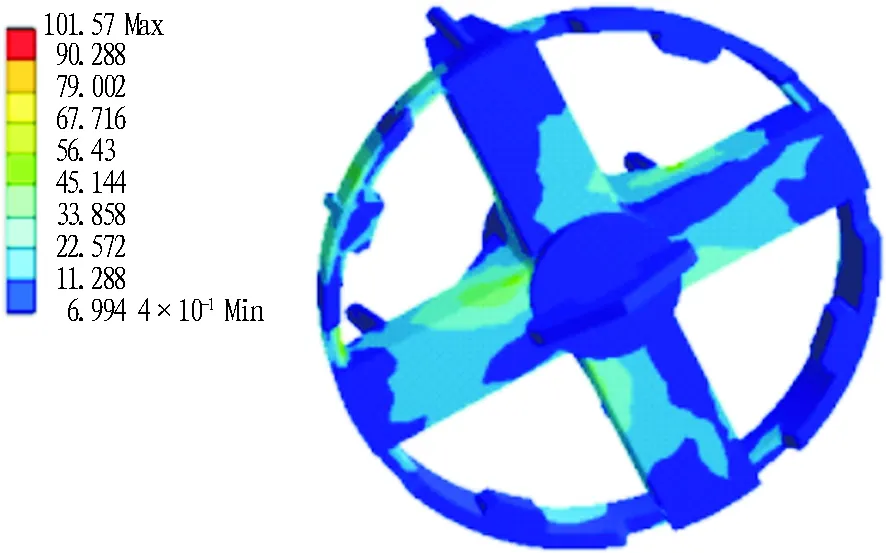
(a) 应力云图(单位： MPa)

(b) 变形云图(单位： mm)

Fig. 8 Finite element analysis of cutterhead under load of bite broken cobble

2.2 砂卵石层刀盘结构减阻优化研究

上述刀盘结构在富水砂卵石地层施工过程中，刀盘前方改良效果不好，渣土流动性差，大量卵石沉积在土舱下部，而刀盘外圈加强大圆环又影响了刀盘垂直方向的开口率，卵石渣土在垂直平面的各个方向上流动受阻，就会因堆积而造成刀盘前部切削阻力过大，尤其是在底部区域。为了解决此问题，本工程试验中对φ2 200 mm、φ1 630 mm 2种刀盘进行结构优化，通过全部或部分切除刀盘加强大圆环，降低刀盘转矩，并对改造后的刀盘降扭效果进行工程试验分析。

2.2.1 刀盘结构优化及有限元分析

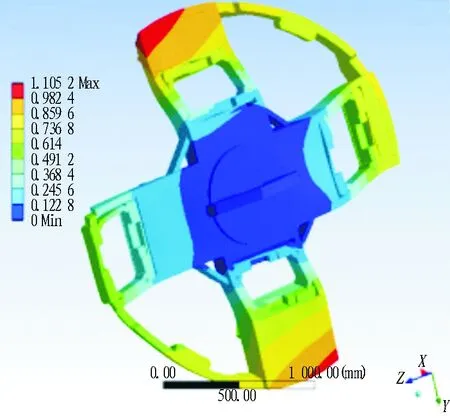
为了确认刀盘结构调整后其强度和刚度是否依然满足要求，采用ANSYS WORKBENCH分别对φ2 200 mm、φ1 630 mm刀盘大圆环对称切除及全部切除的状态进行有限元仿真分析。φ2 200 mm刀盘主要受力刀具为分布在辐条上的切刀以及位于刀箱中的滚刀，进行滚刀计算时将滚刀刀箱与辐条简化为一体。刀盘承受的轴向推力为前方土体传递过来的土压力(根据顶管机设计规范，土压力值一般取为50 t/m2)，以均布载荷方式施加于辐条面板上； 刀盘承受最大转矩取主驱动额定转矩(472.5 kN·m)，作用在整个面板上，约束刀盘筒体圆环内表面全部自由度。φ2 200 mm对称半切除大圆环和全部割除大圆环有限元分析应力及变形云图分别如图9和图10所示。仿真结果对比如表1所示。

(a) 应力云图(单位： MPa)

(b) 变形云图(单位： mm)

Fig. 9 Finite element analysis ofφ2 200 mm cutterhead with semi-excision annulus

φ1 630 mm刀盘承受的轴向推力同样选择为50 t/m2，刀盘承受最大转矩取主驱动额定转矩183 kN·m，在上述约束条件一致的条件下，分别对对称半切除圆环和全部切除圆环进行仿真分析，结果对比如表2所示。

由表1可知： 在边界条件一致的情况下，φ2 200 mm刀盘大圆环全切除和半切除状态下应力差别较大，其中大圆环半切除时最大屈服应力小于Q345B材料许用应力(230 MPa)，最大应力出现在辐条与中心刀盘筒体接触位置，通过进一步的圆角处理或增加筋板的形式，可满足强度要求。由表2可知： 在边界条件一致的情况下，φ1 630 mm刀盘大圆环全切除和半切除状态下应力应变变化不大，应力均<230 MPa，且变形率均小于0.1%，即2种形式均可满足刀盘的强度和刚度要求。综上，将刀盘结构优化方案定为下部φ2 200 mm刀盘大圆环对称半切除、φ1 630 mm刀盘大圆环全切除，如图11所示。

(a) 应力云图(单位： MPa)

(b) 变形云图(单位： mm)

Fig. 10 Finite element analysis ofφ2 200 mm cutterhead with all-excision annulus

表1不同工况下φ2 200刀盘强度和刚度比较

Table 1 Comparison of strength and stiffness ofφ2 200 mm cutterhead in different working conditions

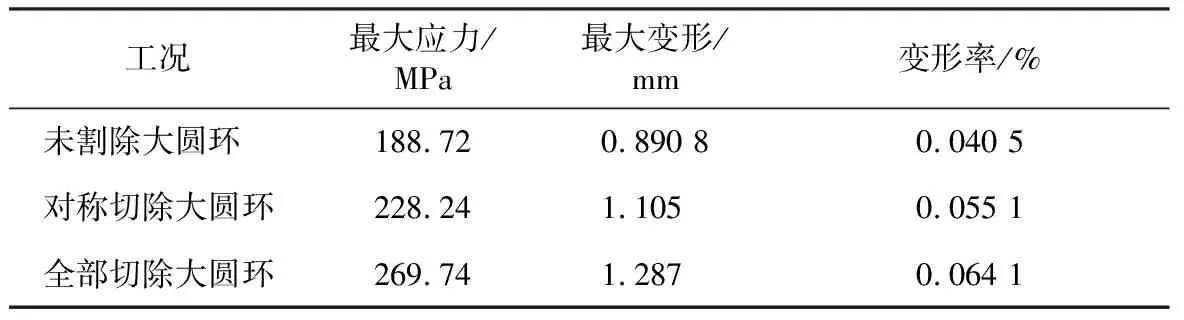
工况最大应力/MPa最大变形/mm变形率/%未割除大圆环188.720.890 80.040 5对称切除大圆环228.241.1050.055 1全部切除大圆环269.741.2870.064 1

表2不同工况下φ1 630 mm刀盘强度和刚度比较

Table 2 Comparison of strength and stiffness ofφ1 630 mm cutterhead in different working conditions

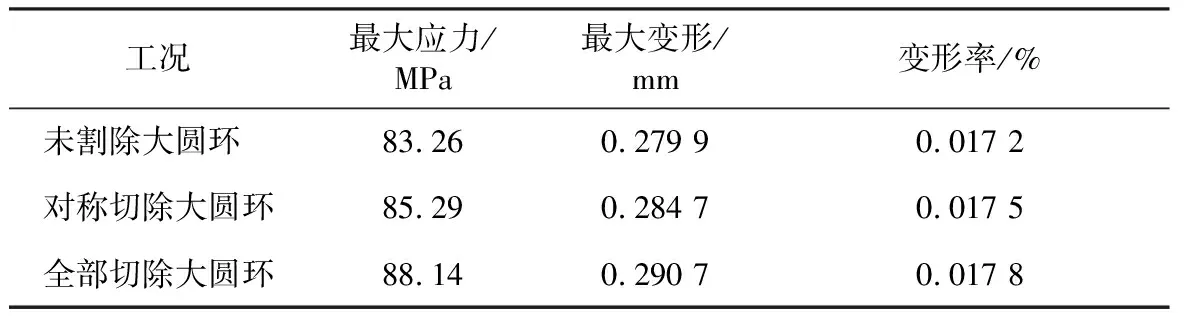
工况最大应力/MPa最大变形/mm变形率/%未割除大圆环83.260.279 90.017 2对称切除大圆环85.290.284 70.017 5全部切除大圆环88.140.290 70.017 8

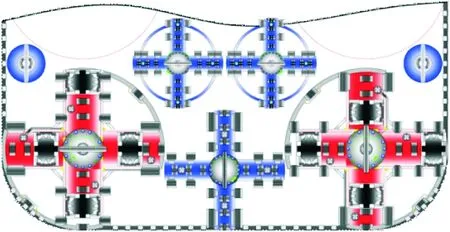
图11 刀盘结构优化方案

此外，为避免刀盘大圆环切割后两相邻刀盘旋转卡卵石，通过刀盘转向PLC协同控制参数设定，确保两两相邻刀盘反向转动。

2.2.2 刀盘结构优化前后掘进转矩对比分析

将刀盘切除圆环优化前后转矩数据记录绘制曲线，如图12所示。由图12可知： 2组刀盘在结构优化后转矩均明显减小，降低20%左右，说明通过切割大圆环增大刀盘的开口率能够有效降低刀盘转矩，解决了下部驱动因转矩过大而经常跳停的问题，进而提高了刀盘切削效率。同时，也从另一角度说明设计阶段所采用的常规刀盘转矩计算经验公式T=αD3不适合作为砂卵石层小刀盘的设计依据，其转矩配置值得进一步的探索。

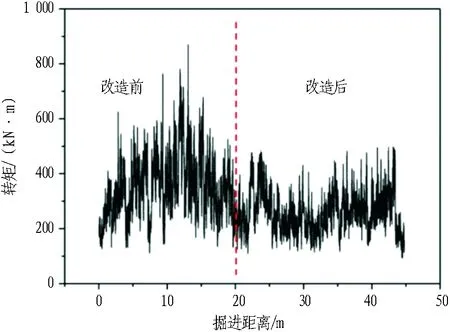
(a) φ2 200 mm刀盘

(b) φ1 630 mm刀盘

3 大粒径卵石双螺旋输送机出渣技术研究

为应对砂卵石地层中直径较大的卵石，采用大直径(706 mm)、大节距(650 mm)带式双螺旋输送机设计，形成以排为主、以破为辅的排渣机制，工程试验中实现排出最大粒径450 mm的卵石。

砂卵石地层情况复杂，在工程试验中出现了排渣不畅、闸门封堵不严的问题。这是由于卵石渣土流动性差，加之砂卵石的骨架效应堵塞出渣口，仅靠土舱压力难以直接进入螺旋输送机，造成排渣不畅，而且螺旋输送机闸门处卵石堆积容易造成插板式闸门不能完全关闭，稀浆易外漏，严重影响主机内部施工环境。对此，分别对螺旋叶片安装位置及螺旋输送机闸门装置结构进行优选试验。

3.1 螺旋叶片安装位置优化

通常螺旋叶片安装位置可分为伸入土舱和不伸入土舱2种设计： 螺旋叶片伸入土舱可实现土舱渣土的主动取土，但会干扰刀盘搅拌棒布置，影响叶片伸入位置在刀盘圆周上的渣土搅拌； 螺旋叶片不伸入土舱采用被动取土形式(依靠土舱压力将渣土压入，要求渣土流动性要好)，土舱内渣土搅拌较为充分。为探索砂卵石层螺旋叶片的适应性，对螺旋输送机螺旋叶片安装位置进行优选试验(见图13)： 方案1为螺旋叶片端头与土舱隔板平齐，不外伸； 方案2为螺旋叶片端头沿着轴线方向伸出隔板进入土舱200 mm。在刀盘转速、土舱压力、螺旋输送机转速一定的条件下分别对2种螺旋输送机叶片位置形式进行工程试验，试验结果如图14所示。由图14可知： 螺旋叶片未伸入土舱设计时，对流动性相对较差的砂卵石层出渣效率较低，卵石渣土仅仅依靠土舱压力很难被螺旋叶片排出，在土舱下部堆积较为严重； 螺旋叶片外伸后掘进速度明显提高，出渣速度也有明显加快。对比发现，螺旋叶片伸入土舱较为适应砂卵石层出渣，其可依靠外力将渣土携带排出，螺旋输送机的主动排渣能力得到大幅提升(提高3倍左右)。

(a) 优化前

(b) 优化后

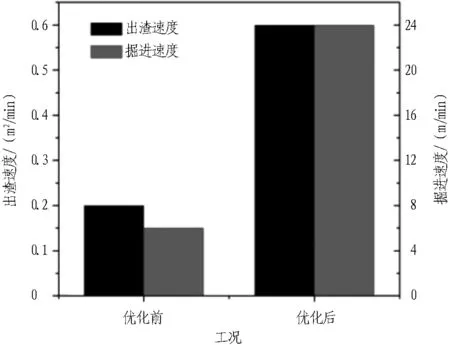
图14 螺旋输送机叶片位置优化前后掘进情况对比

Fig. 14 Excavating situation comparison before and after screw blade position optimization

3.2 闸门装置优化

考虑到常规插板式闸门(即便是双道插板式闸门)在卵石地层中常由于闸门位置的卵石堆积造成闸门不能完全关闭，遂将通常的螺旋输送机第2道插板式密封闸门结构优化为弧形密封闸门，将闸门位置由螺旋输送机筒节中部移动至筒节端部，将闸门位移形式由直线运动改为旋转运动，弧形闸门不仅避开了筒节兜渣位置，采用连杆摇臂机构也解决了闸门油缸安装不方便的问题。2种闸门结构如图15所示。

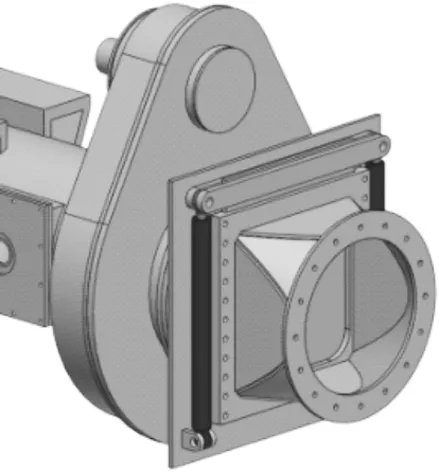
(a) 插板式密封闸门

(b) 弧形密封闸门

分别对2种螺旋输送机密封闸门形式进行工程试验，在成都下穿人民南路第1个矩形顶管项目中采用了单插板式密封闸门，如图16所示，出现了密封不佳的问题，时常发生闸门关不死、向外流水现象。而后采用插板式闸门+弧形密封闸门的设计，如图17所示。根据现场应用情况，弧形密封闸门能够实现设备停机时对富水砂卵石渣土及水有效封挡，解决了常规单一插板式闸门出现的漏渣问题，在成都第2个矩形顶管项目(星汉北路地下通道项目)中得到成功应用。

图16 插板式闸门

图17 插板式闸门+弧形闸门

4 结论与讨论

1)通过对刀盘卵石冲击影响分析，探索出适应砂卵石地层的同平面刀盘开挖形式，避免了前后刀盘布置卡卵石现象的发生。同时研究了砂卵石层下部刀盘减阻技术，通过ANSYS WORKBENCH仿真分析方法对刀盘进行结构优化，下部刀盘通过简化大圆环支撑结构，在满足开挖功能的同时切削转矩降低20%左右。

2)研究了砂卵石层带式双螺旋输送机排渣技术，对螺旋叶片安装位置进行优选试验，试验表明螺旋叶片伸入土舱设计可有效提高螺旋输送机携渣能力，辅以大直径、大节距螺旋叶片设计,有效改善了砂卵石地层的排渣效果，实现了450 mm粒径卵石的顺利排出； 此外，通过对螺旋输送机闸门结构形式的优选试验，表明在砂卵石地层中，弧形闸门装置较插板式闸门能够对渣土实现更好封堵。

3)本文虽然研究出了适用于富水砂卵石地层的矩形顶管机切削系统，但工程试验也印证了设计阶段所采用的常规刀盘转矩计算经验公式T=αD3并不太适合作为砂卵石层小刀盘的设计依据，其转矩配置大小值得进一步探索，如适当放大转矩安全系数或在上述公式基础上引入刀盘尺寸大小的修正因子等。

参考文献(References)：

[1] 彭立敏, 王哲, 叶艺超, 等. 矩形顶管技术发展与研究现状[J]. 隧道建设, 2015, 35(1): 1.

PENG Limin, WANG Zhe, YE Yichao, et al. Technological development and research status of rectangular pipe jacking method[J]. Tunnel Construction, 2015, 35(1): 1.

[2] 贾连辉. 超大断面矩形盾构顶管设计关键技术[J]. 隧道建设, 2014, 34 (11): 1098.

JIA Lianhui. Key technologies for design of super-large rectangular pipe jacking machine[J]. Tunnel Construction, 2014, 34(11): 1098.

[3] 贾连辉. 矩形顶管在城市地下空间开发中的应用及前景[J]. 隧道建设, 2016, 36(10): 1269.

JIA Lianhui. Application of rectangular pipe jacking machine to urban underground space development and its prospects[J]. Tunnel Construction, 2016, 36(10)： 1269.

[4] 川合一成, 南敬. 矩形シ一ルドの開発[J]．コムツテクニカルレポ一ト, 2002, 47(3): 46.

KAZUNAFI Kawai，TAKASHI Minami. Development of rectangular shield[J]. Technical Report, 2002, 47(3): 46.

[5] 王晓睿, 周峰, 张振, 等. 超大断面矩形顶管隧道施工动态变形规律[J]. 地球科学, 2016, 41(11): 1959.

WANG Xiaorui, ZHOU Feng, ZHANG Zhen, et al. Dynamic deformation of the oversized cross-section rectangular pipe-jacking tunnel[J]. Earth Science, 2016, 41(11): 1959.

[6] 杨书江, 孙谋, 洪开荣. 富水砂卵石地层盾构施工技术 [M]． 北京: 人民交通出版社， 2011.

YANG Shujiang, SUN Mou, HONG Kairong. Construction technology of shield tunnel in water rich sandy cobble strata[M]. Beijing: China Communications Press, 2011.

[7] 滕丽, 张桓. 盾构穿越砂卵石地层地表沉降特征细宏观分析[J]. 岩土力学, 2012, 33(4): 1141.

TENG Li，ZHANG Huan. Meso-macro analysis of surface settlement characteristics during shield tunneling in sandy cobble ground[J]. Rock and Soil Mechanics, 2012, 33(4): 1141.

[8] 赵志涛, 张子新, 朱叶艇. 砂卵石-砂土复合试样大三轴数值试验及验证[J]. 地下空间与工程学报, 2014, 10(6): 1300.

ZHAO Zhitao, ZHANG Zixin, ZHU Yeting. Numerical and experimental study of large-scale triaxial tests on sandy cobble-sand samples[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(6): 1300.

[9] 范磊. 富水砂卵石地层矩形顶管机的研究及应用——结合成都川大下穿人民南路人行通道工程[J]. 隧道建设, 2017, 37(7): 899.

FAN Lei. Study and application of rectangular pipe jacking machine to pedestrian passageway on South Renminlu crossing underneath Sichuan University in Chengdu with water-rich sandy cobble strata[J]. Tunnel Construction, 2017, 37(7): 899.

[10] 王小涛, 贾连辉, 贺开伟. 矩形顶管机刀盘的设计讨论[J]. 城市建设理论研究, 2013, 3(13): 183.

WANG Xiaotao, JIA Lianhui, HE Kaiwei. Discussion on design of cutterhead of rectangular pipe jacking machine [J]. Urban Construction Theory Research, 2013, 3(13): 183.

[11] 曹钧, 沈志康, 胡永乐， 等. 冲击作用下岩石破碎比功理论分析及模糊预测模型[J]. 岩土力学, 2012, 33(增刊2): 145.

CAO Jun, SHEN Zhikang, HU Yongle, et al. Theoretic analysis of specific power of broken hard rock by impact action and its fuzzy prediction model[J]. Rock and Soil Mechanics, 2012, 33(S2): 145.