基于零膨胀模型的江苏省AIDS发病研究△

张倩媛 林 晓 朱惠红 言方荣

(中国药科大学生物统计与计算药学研究中心 南京 210009)

在流行病学研究中，对于疾病的发病情况经常有可能出现漏报、瞒报等情况，导致统计数据中出现大量的零数据，这时利用泊松、负二项模型进行分析将可能导致结果出现较大偏差，即发生了零膨胀(Zero-inflated,ZI)现象。通过构建ZI模型可以很好地解决这个问题。近年，ZI模型引起了广泛关注，并被日渐广泛应用于众多领域，成为当今数据分析领域的一大热点[1]。

江苏省是国内艾滋病(AIDS)主要流行省份之一，近年来流行日趋严重[2]，因此对其发病成因的深入研究具有非常重要的意义。本文的研究对象为2004～2010年江苏省艾滋病调查数据。从图1可知，发病次数为零的数据过多，占总体的42.22%，分布较离散，并不满足一般的泊松、负二项模型，具有零膨胀现象。因此，本文针对这类具有零膨胀特性的流行病学数据，结合其流行病学因素变量，构建零膨胀模型，并对AIDS形成及流行原因进行深入分析。

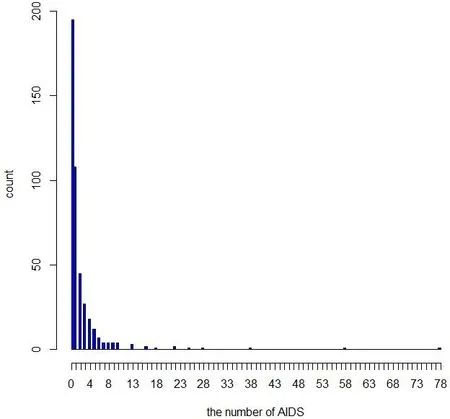
图1 江苏省AIDS发病次数总体直方图

1 模型与评价方法

ZI模型主要包括两部分，分别是零过程和计数过程。零过程的取值只能为0，解释了模型中过多零产生的可能原因；而计数过程取值可为0或正次数，表明因素影响事件发现了多少次[3]。

当计数过程服从泊松分布时便构成了ZIP模型：

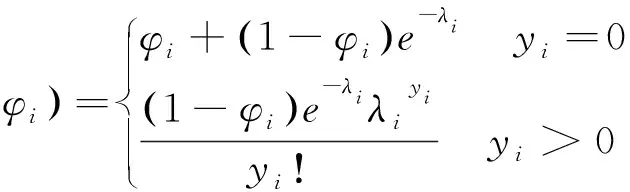
(1.1)

而ZINB模型适用于过离散(方差大于均值)的数据，主要是计数变量为负二项分布时产生，其模型的形式如下：

f(yi,λi,φi)=

(1.2)

在ZIP、ZINB模型中，分别在其参数φi、λi中引入协变量而构建回归方程。

对于ZI模型，参数估计通常采用广义线性模型框架下的极大似然估计来实现[4]，通过最大化对数似然函数而得到参数的估计值。

2 实证分析

2.1 数据描述

本文研究对象为江苏省63个市县在2004～2010年的艾滋病发病记录，包括发病率(1/10万)、农村人口数(万人)、人均GDP(万元)、人口数(万人)、卫生机构对数共5个变量，441个观测。此外，根据人口数和发病率计算得到发病次数(例)，产生用于分析的数据集。

表1 艾滋病发病数据概况

变量样本量均值中值方差变异系数(%)最小值最大值发病次数4412.152134.356272.381078农村人口数44180.798781460.97047.3075.080253.890人均GDP4413.4512.4259.13287.554.39221.898人口数441113.120102.3605259.95064.11427.240547.170卫生机构对数4412.3172.230.23120.7301.4313.625

从表1的描述性统计分析可知：变量农村人口数、人口数波动较大，为了消除量纲影响和变量变异大小的影响，本文对协变量进行标准化处理。

2.2 模型分析

2.2.1最优模型选择

(1)过离散检验

O=221.97远大于1.96，且发病数的方差远大于均值(34.356>2.44)，表明数据呈现过离散现象，说明对此展开的分析中，NB模型应优于Poisson模型，ZINB应优于ZIP。

(2)模型拟合评价指标

运用R软件构建了4类模型，通过表2进一步证实：ZINB、NB模型均优于ZIP和Poisson模型，而ZINB较NB更优一些。

表2 各模型的拟合评价指标及比较结果

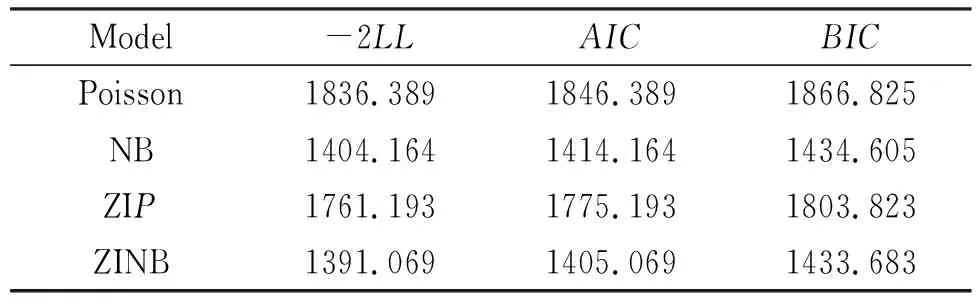
Model-2LLAICBICPoisson1836.3891846.3891866.825NB1404.1641414.1641434.605ZIP1761.1931775.1931803.823ZINB1391.0691405.0691433.683

(3)Vuong检验统计量结果

表3 Vuong检验结果

Model1-Model2V值P值模型选择ZIP-Poisson2.7730.003ZIP>PoissonZINB-NB1.8720.031ZINB>NB

通过V检验可知，ZIP模型优于Poisson模型，ZINB模型优于NB模型，综合模型拟合评价指标可知：ZINB模型是最佳模型。

2.2.2ZINB模型分析结果

ZINB模型包括两部分内容：Logit部分、负二项部分，回归结果见表4。其中，Logit部分是以艾滋病不发生为响应概率，逆向考察了哪些因素影响了艾滋病的发生；而负二项部分基于此，进一步分析与艾滋病发生次数相关的影响因素，参数估计值为正表明随自变量取值变大，艾滋病发病次数增加。

表4 ZINB回归分析结果

过程参数参数估计标准误Z值P值负二项部分(计数过程)Intercept0.3150.0724.356 1.33e-05#nc_num0.4370.0904.864 1.15e-06#GDP_mean0.5750.0688.512<2e-16#population0.2660.0813.2850.001**Logit部分(零过程)Intercept-7.7423.068-2.5230.012*GDP_mean-8.3183.475-2.3940.017*

注：#P<0.001；**P<0.01；*P<0.05。

负二项部分的模型说明了人均GDP、人口数、农村人口数均对艾滋病发病次数的多少有显著的影响，且均呈现正相关的关系，说明了经济发达地区较经济欠发达的地区，人口密集区域较人口稀少区域，农村人口稠密区较农村人口稀疏区，艾滋病的发病率都更高一些。其中，人均GDP的影响最大(系数为0.575)，因此，应首要加强经济发达地区的艾滋病防治工作，并要重点关注于人口密集，或是农村人口密集的地区的艾滋病情况。

3 讨论

相对于传统的计数模型如Poisson、NB模型，ZI模型从艾滋病发病数的角度研究与艾滋病发病有关的影响因素，能够更充分地利用数据的有效信息，更适合拟合含有零过多的数据。

本文针对江苏省2004～2010年间63个市县的艾滋病发病情况，基于4个与流行病学相关的协变量，建立了Poisson、NB、ZIP和ZINB 4个模型，并得出ZINB回归模型是最优模型的结论。其中，在本文所建立的ZINB回归模型中，人口密集区域、农村人口稠密市县，其艾滋病发病率是显著增加的。因此，着重对苏南等经济发达城市、发病热点区域、人口密集地区以及农村人口稠密市县等进行合理防治和严格把控是艾滋病治理的有效手段。

1 解锋昌,韦博成,林金官,等.ZI数据的统计分析综述.应用概率统计,2009,25(6):659～671.

2 刘文东,朱叶飞,吴莹,等.江苏省HIV/AIDS时空流行特征分析.中国卫生统计,2014,31(3):383～386.

3 赵晶,所佳宁,罗潇,等.基于零膨胀模型的阳性过敏原数影响因素研究.中国卫生统计,2014,31(5):853～855;859.

4 Ceppi M,Biasotti B,Fenech M,et al.Human Population Studies with the Exfoliated Buccal Micronucleus Assay.Mutation Research,2010,705(1):11～19.

5 Yau KK,Lee AH,Carrivick PJ.Modeling Zero-inflated Count Series with Application to Occupational Health.Computer Methods Programs Biomedicine,2004,74(1):47～52.

6 Riccardo E,Marionia1,Fiona E, et al.The Association Between Late-life Cognitive Test Scores and Retrospective Informant Interview Data.Int Psychogeriatr,2011,23(2):274～279.

收稿日期：2017-07-17