无失效数据的Weibull分布小子样寿命评估模型

赵 远，杨 琳

（1.中国电子科技集团公司第二十研究所， 陕西 西安710068；2.兰州理工大学， 甘肃 兰州 730050）

引言

如何高效地验证航天产品高可靠寿命已成为目前迫切需要解决的工程问题。传统的处理定时截尾数据的统计方法已经不难满足工程需求[1-3]。国内外的专家们都对无失效数据问题展开了研究[4，5]。傅惠民等[2]提出了一种Weibull分布定时无失效数据可靠性分析方法，在形状参数下限已知的情况下，给出了可靠度和使用寿命的单侧置信下限。张勇波等[6]提出了一种Weibull分布定时无失效数据疲劳寿命分散系数修正方法，从疲劳分散系数的定义出发，分别对无失效数据情形下基于平均寿命、特征寿命等疲劳寿命分散系数进行了修正。在对产品某些特定时刻的可靠度具有较多的经验认识基础上，多名专家提出了基Bayes理论的无失效数据的可靠性分析评价方法[7-8]。

针对上述可靠度验证的迫切工程问题，本文开展无失效数据的Weibull分布小子样寿命验证模型研究。通过该模型能够确定Weibull分布函数的形状参数估计区间，并且，进一步得到了产品使用寿命和可靠度的单侧置信下限。最后，以某型产品的可靠寿命验证试验为例，应用该评估模型，给出了后续试验方案，验证了其工程实用性和有效性。

1 无失效数据的寿命验证模型

1.1 验证模型原理

无失效数据的寿命验证模型原理如图1所示。结合寿命试验数据，对Weibull分布的形状参数m进行区间估计。通过引入特征寿命的相对差值和特征寿命变化量的相对差值，来确定m的区间范围。分别确定一定置信水平下的给定可靠度R(t)的最优置信下限寿命。讨论不同试验子样下，需继续试验时间，以选择最优的试验方案来验证产品的可靠寿命。

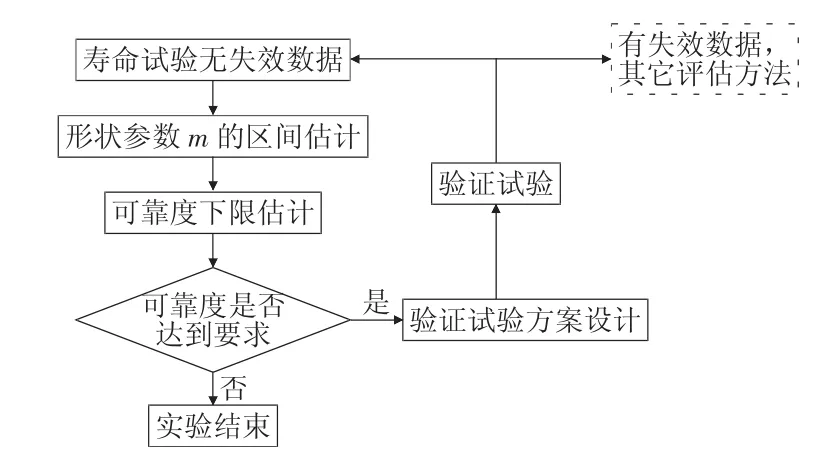
图1 无失效数据的寿命验证模型原理

1.2 无失效数据的寿命验证流程

1.2.1 形状参数估计有n个产品，试验时间为t1≤t2≤…≤tn时未发生故障，其寿命分布函数为

其中，m为形状参数，η为特征寿命。通过指数变换，得到威布尔分布的特征寿命η在1-α置信水平下的单侧置信下限为：

引入特征寿命的相对差值和特征寿命变化量的相对差值来确定m的上下限。

特征寿命的相对差值为：反映了不同形状参数下的特征寿命与最长无失效数据的相对差值，通过设定可接收的特征寿命与最长无失效数据的相对差值范围，即Δ(m)≤0.3，能够确定形状参数m的下限。

特征寿命变化量的相对差值为：

反映了不同形状参数下的特征寿命变化量的相对差值，设定可接受的特征寿命变化量的相对差值范围，ΔηL＜0.01，不同的形状参数 m1和 m2下，特征寿命的变化量相对于试验数据已非常小，m取m1到m2（甚至更大）之间，对特征寿命的预估影响很小。能够确定形状参数m的上限。

通过上述确定的m范围，分别讨论可靠度R（t）的最优置信下限和可靠寿命tR的最优置信下限：

1.2.2 可靠寿命验证试验分析

通过文献[1]可知，

式中而由 m'下述方程得到，其中，ti为试验得到的无失效数据，t为已知给定的工作时间（次数）。

若（5）式的解为 m*，当 m*＜m1时，取 m'=m1；当 m*＞m2时，取 m'=m2；当 m1≤m*≤m2时，取 m'=m*。若（5）式无解，当 t＞tn时，取 m'=m2；当 t＜t*时，取 m'=m1。因此，在m1≤m≤m2的无失效数据情形下，可靠度R（t）在置信水平1-α的最优置信下限为

式中为（5）式的根。

在给定寿命T及其可靠度R0下，在原有试验时间的基础上，假定持续进行x时间（次数）的试验。从而得到无失效数据变为ti+x，通过公式（6）能够使到：

进一步，通过（7）式，能够得到不同样本量k（k=1,…,n）下，的继续试验时间，在结合试验成本、进度要求，选择最有利的试验方案，来验证产品的可靠寿命。

2 实例

以某型产品0.8置信水平下，5 500次点火的可靠度置信下限为0.98的验证过程为例，来说明该验证模型的工程有效性和可行性，该产品点火试验数据如表1所示。

表1 试验结果

2.1 寿命评估

1）确定m的下限值。将4组数据代人到公式（2）中，在80%置信水平下，分别计算了11个形状参数所得到的特征寿命和相对差值，如表2所示。通过特征寿命与最大点火次数的相对差值，Δ(m)≤0.3，确定m的下限为3。

2）确定m的上限值。进一步得到了形状参数m与特征寿命η之间的关系，分别计算了m分别取9和30下的特征寿命。特征寿命η（9）与η（30），仅相差了48次，远小于设备点火总次数（目前已开10 000次量级）的0.5%。并且，m取9到30（甚至更大）之间，对特征寿命的预估影响很小。为了便于在无失效数据下的产品点火次数进行评估，取产品点火次的寿命形状参数m的上限为9。

现计算在0.8的置信水平下，产品点火5500次时可靠度得置信下限。通过公式（6）得

表2 不同形状参数下的特征寿命与方差

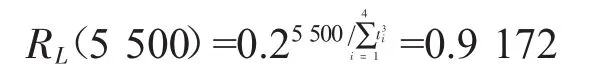
2.2 验证试验方案分析

通过（7）式，得到后续试验次数与可靠寿命置信下限得关系式

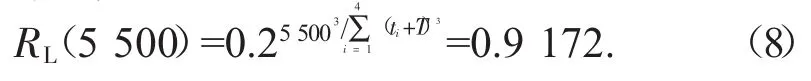
计算得到后续开展5 805次无失效点火循环试验，能够验证考核目标。

通过公式（8）给出了不同试验方案：不同试验样本量的点火循环次数与可靠度下限验证方案的对比，试验人员可以根据时间进度、成本和场地等因素进行权衡，以选择相应的试验方案。

3 结论

为了高效地验证高可靠、长寿命产品的可靠寿命，本文提出了一种无失效数据的Weibull分布小子样寿命验证模型，该模型有以下优点：

1）通过试验的无失效数据，在一定的置信度下得到了Weibull形状参数区间，进一步得到产品的可靠性特征结果。

2）在形状参数区间估计的基础上，对试验方案（试验时间和子样）进行优化分析。

3）本文的模型既能充分利用无失效数据的寿命信息，又能发挥Weibull分布无失效数据可以累加的优点。

4）本文的计算方法简单，便于工程应用。

[1]赵宇.可靠性数据分析[M].北京：国防工业出版社，2014.

[2]傅惠民，张勇波.Weibull分布定时无失效数据可靠性分析方法[J].航空动力学报，2012，25（12）：2 807-2 810.

[3]王景芹，唐义良，陆俭国.小子样及无失效数据时电器产品可靠性特征量的估计[J].电工技术学报，2000，15（4）：27-31.

[4]韩明.无失效数据可靠性进展[J].数学进展，2002，31（1）：12-15.

[5]韩明.产品无失效数据的综合处理[J].机械工程学报，2003，39（2）：129-132.

[6]张勇波，傅惠民，王治华.Weibull分布定时无失效数据寿命分散系数[J].航空动力学报，2012，27（4）：795-800.

[7]蔡忠义，陈云翔，项华春，等.基于无失效数据的加权E-Bayes可靠性评估方法[J].系统工程与电子技术，2015，37（1）：219-223.

[8]刘鸿铭.无失效数据下复杂系统可靠度的Bayes估计[D].哈尔滨：哈尔滨理工大学，2014.