纤维混凝土双丝拉拔物理实验与三维数值模拟*
2018-06-07刘浩曾向荣张亚芳梁正召
刘浩,曾向荣,张亚芳,梁正召
(1.深圳市市政设计研究院有限公司,广东深圳518029;2.广州大学土木工程学院,广东广州510006;3.大连理工大学土木工程学院,辽宁大连116024)
界面是复合材料的重要组成部分,界面相的力学性能影响构件宏观力学性能[1-2]。许多学者运用单丝拉拔物理实验[3-5]研究了纤维增强混凝土界面力学性能并取得了不少进展,目前也有一些单丝拉拔数值模拟研究成果[6-8]。但由于多丝拉拔试验装置设计与实验过程的复杂性,加之多丝拉拔数值模型分析也极为复杂,因此鲜见双丝拉拔的物理实验和数值模拟研究成果的报道。实际上,纤维增强混凝土构件往往存在多丝间的强耦合作用,耦合效应不可忽略[9-10],而单丝拉拔无法表征这种多丝间的相互作用。因此,开展双丝拉拔的研究具有重要的理论研究价值与实际应用意义。本研究通过设计双丝模型的模具并进行加工,开展了双丝拉拔物理力学实验研究,并采用三维数值试验方法模拟了双丝拉拔过程,研究了埋深对双丝拉拔过程及宏观力学性能的影响。
1 物理实验过程
相对于单丝拉拔实验,双丝拉拔实验的加载模具与实验过程更为复杂。目前已有的单丝拉拔设备对于双丝拉拔实验存在诸多不足和限制:一是双丝拉拔试件的制备;二是加载过程中如何实现平行加载,避免偏心加载带来的误差。针对上述要求,需要对钢丝进行处理并自行设计和加工加载模具,图1为加载模具装配图。

图1 模具装配图Fig.1 Setting of the steel mould
如图1中(a)所示,首先对钢丝进行处理,在钢丝末端刻上螺纹,方便拧上螺栓。图1中(b)的T型钢模具用于固定双丝并与加载机下夹头相连。首先在双丝螺纹一端各自拧上螺栓,两螺栓相互平行,以保证螺栓约束加载模具顶板。然后双丝穿过加载钢模具的开口槽,再在双丝螺纹端拧上螺栓,使螺栓约束模具顶板底面,使得构件及加载模具不能移动,如图1中(c)所示。最后把基体放入固定基体的钢模具中,此模具是用于固定基体并与加载机上夹头连接,装配好的构件如图1中(d)所示。本文开展的双丝拉拔物理实验中,钢丝选取直径为8 mm的光圆钢筋替代,这是因为钢筋与混凝土的结合机理及钢丝与混凝土的结合机理是相同的[11]。采用广宇牌复合硅酸盐水泥制备混凝土,混凝土强度为C30。
利用SANS微机控制电液伺服万能加载机对构件进行加载,如图2所示。把装配好的构件与加载机连接,在主控计算机中选择位移加载方式,加载速率为0.02 mm/min,共加载5 mm后停止,获得双丝拉拔构件的荷载-位移曲线。

图2 加载机及加载原理Fig.2 Testing apparatus and loading process
2 数值模拟模型建立
数值模拟中构件的尺寸为40 mm×40 mm×40 mm,钢丝直径为2 mm,双丝中心距为8 mm,界面层厚度为0.1 mm。采用拉位移加载方式,加载速率为0.000 1 mm/步。分别计算了埋深为5、10、15、20、25、30和35 mm共计7组双丝构件。数值模型利用 ANSYS的建模功能来完成,采用SWEEP命令对模型进行有限元划分,共划分约130万个单元,并对模型施加荷载约束。在ANSYS中输入相应的宏命令,导出模型信息,再把模型导入到RFPA3D系统中,获得了如图3所示的数值模拟模型。本文采用了线弹—脆性细观本构关系来对基体单元和纤维体单元进行描述,对界面体单元建立了基于各向异性特征的本构模型,以实现随机概率模型。
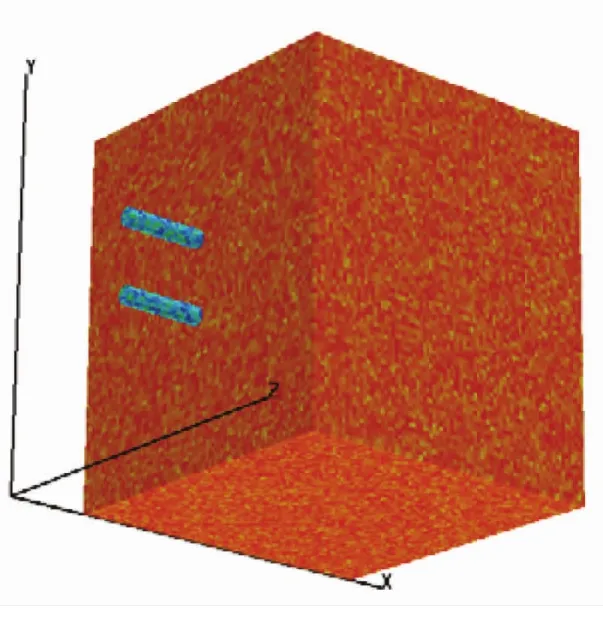
图3 三维数值模型Fig.3 3D Model
RFPA系统引入双参数 Weibull分布函数来描述细观单元的力学性质,从而体现材料的非均匀性。Weibull分布函数的表达式为:
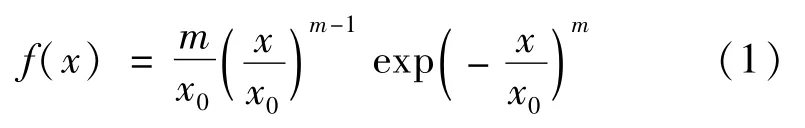
式中,m为均质度,反应了材料的均匀分布程度。x0为单元力学性质参数平均值,各相材料的参数选取参照文献[12]。
3 结果讨论
3.1 物理实验结果讨论
图4是双丝拉拔构件物理实验的荷载-位移曲线及数值模拟计算获得的荷载-位移曲线,对曲线进行归一化处理,取峰值荷载为1。图4中(a)为物理实验结果。在加载之初,双丝构件处于弹性阶段,荷载-位移曲线表现为线弹性,曲线光滑。当位移荷载到达0.9 mm时,曲线出现波动,但曲线形态仍为线性,此时构件内部界面出现损伤并伴随滑动摩擦力出现。当位移到达1.4 mm附近时,曲线进入平台段,构件界面进入塑性变形阶段,荷载不随位移增大而增大。平台段结束后,曲线进入近似线性增强段,此过程位移增加,荷载增加。到达峰值荷载后,曲线进入劣化段,此时钢丝脱黏,构件发生失稳破坏。
图4中(b)为数值模拟分析获得的荷载-位移曲线。结合图4(a)可知,物理实验与数值模拟结果形态相似,曲线形态可归纳为3个阶段,即线弹性段、非线性增强段及荷载劣化段。因数值模拟分析忽略钢丝与基体间的滑动摩擦,所以获得的曲线是光滑的。
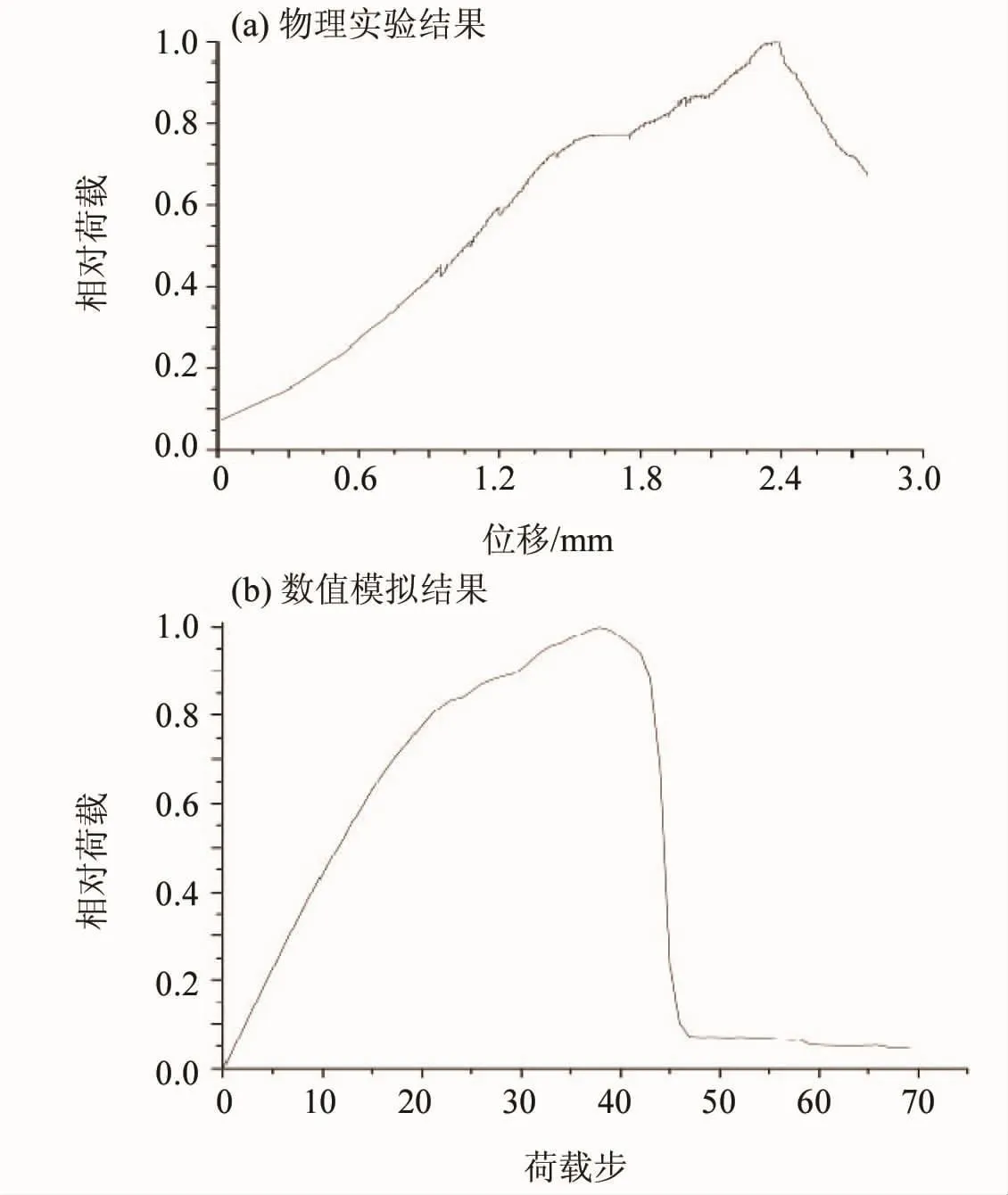
图4 物理实验及数值模拟荷载-位移曲线Fig.4 Load-displacement curves of experienment and simulation
根据数值模拟及物理实验的结果,可将双丝拉拔构件的荷载-位移曲线简化为三线性本构模型,即线弹性段,线性增强段及荷载劣化段,本构简化公式及简化模型如公式(2)及图5所示。

式中,f代表荷载,u代表位移,f1、f2分别代表弹性段结束时的荷载及峰值荷载,u1、u2代表弹性段结束时的位移及到达峰值荷载时的位移。
3.2 数值模拟结果讨论
图6分别给出了埋深为5及35 mm的双丝构件的拉应力云图,这两种构件分别代表埋深较小及埋深较大的构件。如图6所示,两种不同埋深构件的拉应力集中分布区域有其共同特点,即界面附近圆环状区域基体是应力集中区域。埋深增加,双丝间的应力集中现象更明显;如图6(b)所示,双丝间中部基体拉应力斑纹相对于图6(a)更为明亮,这说明埋深增加后双丝和双丝间的基体共同承受拉拔荷载,双丝耦合效应更加明显。
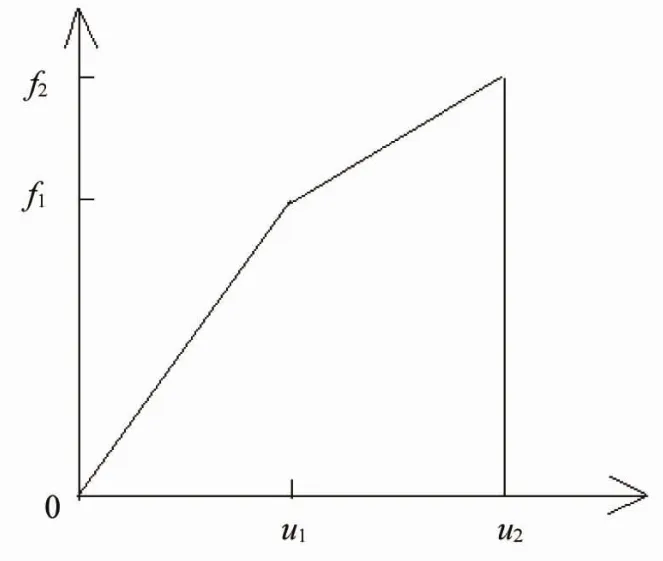
图5 双丝拔出荷载-位移简化模型Fig.5 Load-displacement simple model of double steel bar pull out

图6 拉应力分布图Fig.6 Picture of tensile stress distribution
图7是双丝埋深分别为5、15、25及35 mm 4个构件的荷载-位移曲线。如图所示,双丝埋深变化对构件的荷载-位移曲线的形态影响较大。双丝拉拔构件的荷载-位移曲线主要划分成以下3阶段:线性阶段、非线性强化阶段和劣化段。在线性阶段,双丝构件的持续时间随埋深增加而增加。线性段结束,曲线进入非线性增强段,此阶段双丝埋深对构件荷载-位移曲线影响很大,双丝埋深越大,荷载-位移曲线中非线性强化段持续时间也相应增加。埋深达到35 mm时,曲线的非线性强化段持续时间最长,说明埋深增加延迟了双丝构件失稳破坏时间,提高了构件的整体韧性。构件达到非线性强化阶段的末端,即峰值荷载后,就进入了劣化段,此时荷载急剧下降,构件发生失稳破化,最后仅承受残余荷载。
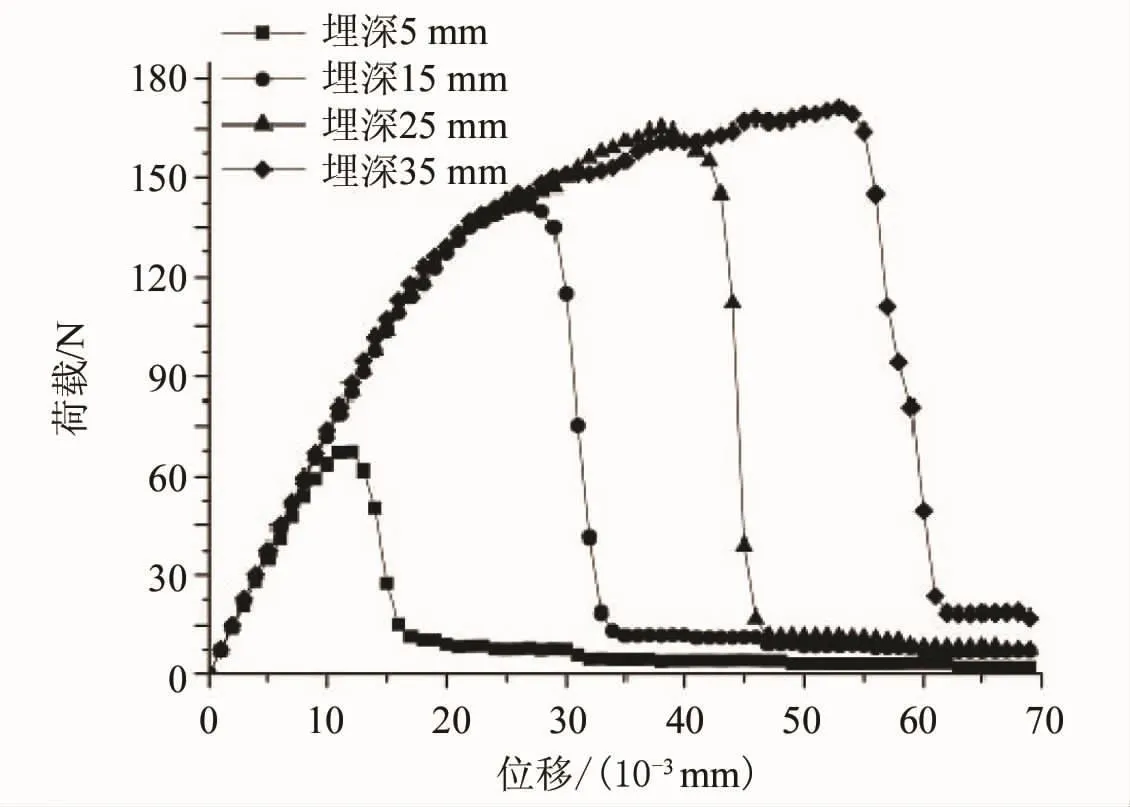
图7 荷载-位移曲线Fig.7 Load-displacement curves
双丝埋深变化对构件的峰值荷载影响明显。图8给出了不同埋深构件的峰值荷载变化图。如图所示,随着双丝埋深的增加,双丝构件的峰值荷载也在不断增加,说明双丝埋深增加能有效提高构件的承载能力,这与 Shannag等[13]及 Jia等[14]学者的研究结果一致。双丝埋深变化与峰值荷载变化的表达式如公式(3)所示,其相关系数是R2=0.962 55,表明数据相关性良好。
Y=27.142 86+10.130 95x-0.176 67x2(3)式中,x为双丝埋深,y为构件峰值荷载。
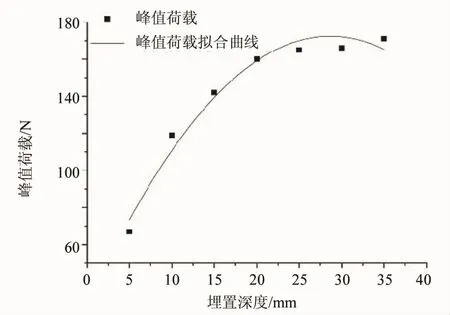
图8 峰值荷载变化图Fig.8 The change of peak load
为进一步探讨埋深控制下双丝构件的增韧效应,分析材料试件的韧度(即试件荷载-位移曲线包围的面积),试件的韧度可以通过对图7中的荷载-位移曲线进行面积积分而得到,并将获得的结果进行归一化处理,取最大值为1,即得到不同埋深构件的相对韧度指标,如图9所示。埋深变化与相对韧度的变化呈线性关系,相对韧度随着双丝埋深增加而不断增加,说明双丝埋深增加能有效提高构件的整体韧性。
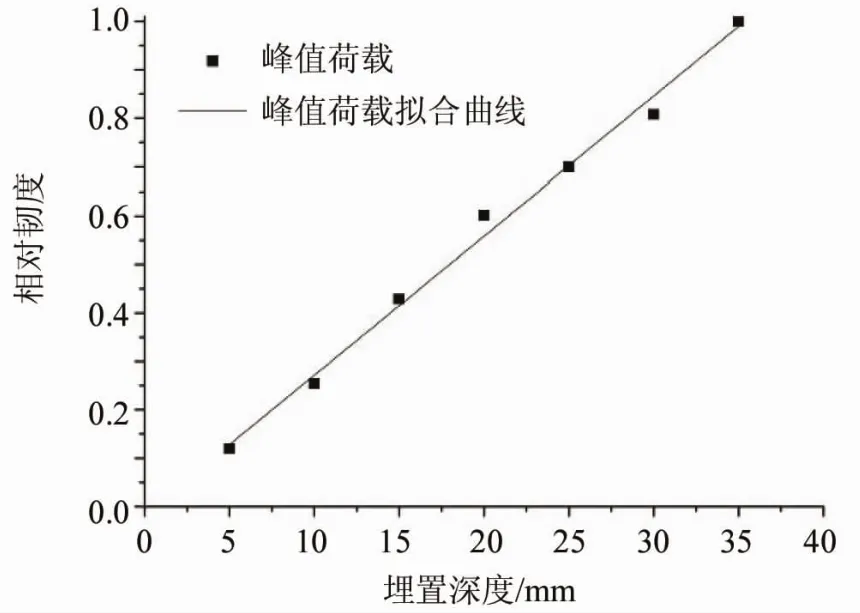
图9 相对韧度图Fig.9 Picture of relative toughness
其拟合关系见式(4)所示,相关系数R2为0.991 65,说明使用线性拟合效果很好,公式如下:
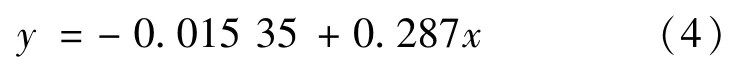
式中,x为双丝埋深,y为相对韧度。运用声发射技术(acoustic emission,简称AE)可以监测材料内部裂纹萌生、扩展乃至失稳破坏全过程[15]。本文数值模拟计算中假设声发射数量与单元损伤量成正比,一旦单元出现损伤破坏,则伴随着声发射出现。
图10是双丝埋深为35 mm构件的声发射演化图。图中气泡大小代表单元声发射能量释放大小。气泡直径越大,说明该点在此加载步的声发射能量释放越大,也证明该点处单元正在发生损伤破坏。如图10所示,在加载初期(Step10,表示有限元计算的第10步,后同),双丝埋入端附近界面气泡直径大,说明此处声发射释放能量大,此处的单元在该加载步发生损伤破坏,使得埋入端附近界面首先脱黏。继续加载,大直径气泡沿界面向纵深方向扩展,而埋入端气泡直径很小,说明损伤过程也在沿界面纵深方向扩展,直至界面埋置端(Step70)。从声发射演化图可以发现,双丝界面脱黏过程是渐进的。
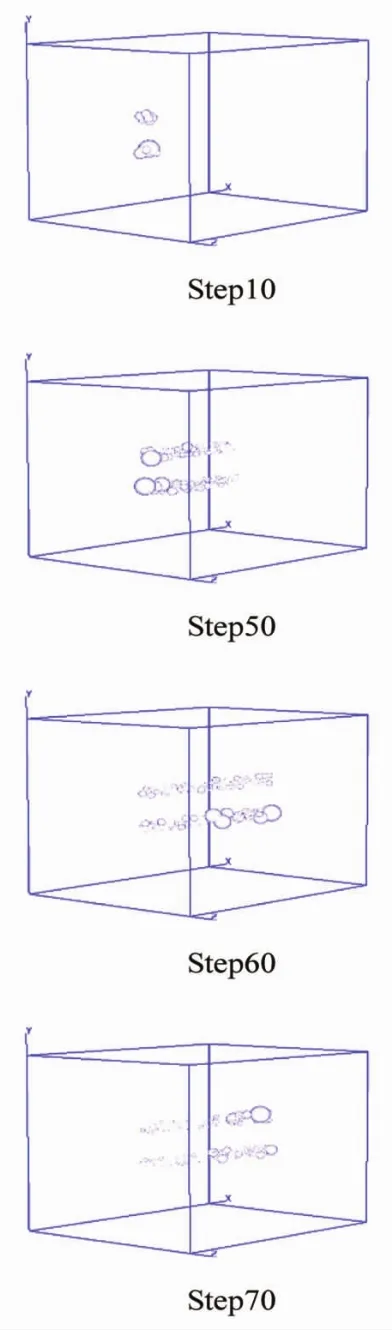
图10 埋深35 mm构件声发射演化图Fig.10 Process of AE evolution of 35 mm embedment
图11分别是埋深5 mm和35 mm双丝构件的荷载—步长—声发射曲线图。两种不同埋深的构件在弹性段下即出现声发射,此时声发射量少,双丝间界面单元出现损伤。弹性段结束,曲线进入非线性增强段,声发射量不断增加,界面出现局部脱黏,从弹性段到非线性增强段之间的声发射计数是稳步上升的。双丝埋深增大后,曲线的非线性增强段持续时间较长,此时绝大部分声发射计数量集中在这一阶段,埋深5 mm构件的声发射计数总数为318,而埋深35 mm构件的声发射计数总数为2 230,是埋深5 mm构件的7倍,说明双丝埋深提高后,拔出过程需要消耗较多的拔出功,双丝埋深增加能有效提高构件的整体拉拔韧性。
4 结 论
本文自行设计并开展了双丝拉拔物理实验,从材料细观非均匀角度出发,建立了三维双丝拉拔数值模型,研究了不同埋深下双丝拉拔构件力学性能的影响。在物理实验中获得了双丝拉拔的荷载-位移曲线,在数值模拟研究中获得了不同双丝埋深下的拉应力云图、荷载-位移曲线及声发射演化过程图等,得到如下结论:

图11 荷载-步长-声发射图Fig.11 Load-step-AE curves
1)物理实验获得的荷载-位移曲线和数值模拟分析获得的荷载-位移曲线具有相似规律,得到了纤维增强混凝土双丝拉拔构件的简化三线性简化本构关系,包括线弹性阶段、线性增强段及劣化段。
2)埋深增加对构件的拉应力分布影响显著,随着双丝埋深的增大,双丝间耦合效应更为明显,双丝与中部基体共同参与承受外荷载。
3)双丝埋深增加能显著提升构件的峰值荷载和韧性。
[1]吴人洁.复合材料[M].天津:天津大学出版社,2000.
[2]黄承逵.纤维增强混凝土结构[M].北京:机械工业出版社,2004.
[3]TAHER A L,SAMEER H,WILLIAM H,et al.Effect of matrix strength on pullout behavior of steel fiber reinforced very-high strength concrete composites[J].Construction and Building Materials,2011,21(1):39-46.
[4]WON J P,HONG B T,LEE SJ,et al.Bonding properties of amorphous micro-steel fibre-reinforced cementitious composites[J].Composite Structures,2013(102):101-109.
[5]VITOR M CF C,JOAQUIM A O B,JOSE M SC.Pullout behavior of steel fibers in self-compacting concrete[J].Journal of Materials in Civil Engineering,2009,22(1):1-9.
[6]马莉,江晓禹,裴永琪.玻璃纤维单丝拔出实验及其有限元模拟[J].材料导报 B:研究篇,2011,25(10):139-142.MA L,JIANG X Y,PEI Y Q.Simulation and analysis of single fibreglass pull-out test with FEM[J].Materials Review B:Research articles,2011,25(10):139-142.
[7]陈沛然,张亚芳,李根.基体强度对钢纤维单丝拉拔性能的影响[J].中山大学学报(自然科学版),2013,52(6):68-80.CHEN PR,ZHANG Y F,LIG.Effect of matrix strength on properties of steel single fiber pull-out test[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2013,52(6):68-80.
[8]彭细荣,杨庆生.纤维拔出实验的样本尺寸效应[J].复合材料学报,2002,19(5):84-89.PENG X R,YANGQ S.Effect of specimen size for fiber pull-out test[J].Acta Materiae Compositae Sinica,2002,19(5):84-89.
[9]张亚芳,曾向荣,刘浩,等.界面控制下间距对双丝拉拔实验影响的数值模拟研究[J].武汉理工大学学报,2015,37(9):78-83.ZHANG Y F,ZENG X R,LIU H,et al.Numerical simulation on twin fibers pull-out test under interfacial control with effect of spacing[J].Journal of Wuhan University of Technology,2015,37(9):78-83.
[10]黄俊,姜弘道.一种新的界面脱粘和纤维拔出模型[J].应用力学学报,2006,23(3):473-478.HUANG J,JIANG H D.A new model of interfacial debonding and fiber pullout[J].Chinese Journal of Applied Mechanics,2006,23(3):473-478.
[11]李丽娟,张红州,刘锋,等.纤维与混凝土粘结的界面力学性能研究[J].新型建筑材料,2004,(10):1-5.LI L J,ZHANG H Z,LIU F,et al.Study on mechanical properties of coherent interface between fiber and concrete[J].New Building Materials,2004(10):1-5.
[12]唐春安,朱万成.混凝土损伤与断裂-数值试验[M].北京:科学出版社,2003.
[13]SHANNAG M J,BRINCKER R,HANSEN W.Pullout behavior of steel fibers from cement-based composites[J].Cement and Concrete Research,1997,27(6):925-936.
[14]JIA Y Y,CHEN Z R,YAN W Y.A numerical study on carbon nanotube-hybridized carbon fibre pullout[J].Composites Science&Technology,2014,91(2):38-44.
[15]张明,李仲奎,杨强,等.准脆性材料声发射的损伤模型及统计分析[J].岩石力学与工程学报,2006,25(12):2493-2501.ZHANG M,LI Z K,YANG Q,et al.A damage model and statistical analysis of acoustic emission for quasibrittle materials[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(12):2493-2501.
