Caputo导数下分数阶Lagrange系统的Noether准对称性与守恒量*

刘艳东，张毅

（1.苏州科技大学数理学院，江苏苏州215009；2.苏州科技大学土木工程学院，江苏苏州215011）

经典力学中许多经典的方法只适用于保守系统，对于非保守系统却不适用。为了解决这一问题，1996年Riewe[1-2]将分数阶微积分引入到非保守系统动力学，开启了非保守系统的分数阶建模及其研究。Frederico和 Torres[3-6]首先开展分数阶Noether定理的研究，利用时间重新参数化方法证明了分数阶力学和控制系统的Noether定理。张毅等[7-13]研究了分数阶Birkhoff系统的Noether对称性与守恒量。近年来，关于对称性与守恒量的研究取得了许多成果[14-19]。但迄今为止，基于Frederico和 Torres定义的分数阶守恒量概念建立的Noether定理仅研究了Noether对称性与守恒量之间的联系，尚未考虑其准对称性。本文将基于Caputo导数用时间重新参数化方法研究分数阶Lagrange系统的Noether准对称性，建立该系统准对称性的定义和判据，给出Frederico-Torres守恒量定义下的分数阶守恒量，并证明该系统的分数阶Noether准对称性定理。

1 分数阶导数及其性质

以下简单介绍文中将用到的分数阶导数的定义及相关性质，具体参见[20-21]。

设函数f（t）在区间[a，b]上连续可积，则Riemann-Liouville分数阶左导数和右导数分别定义为：

其中，Γ（*）是Euler Gamma函数，α是阶数，且0≤α＜1。

设函数f（t）和g（t）是在区间[a，b]上的光滑函数，且f（a）＝f（b）＝0，则Caputo导数下的分数阶分部积分公式为：

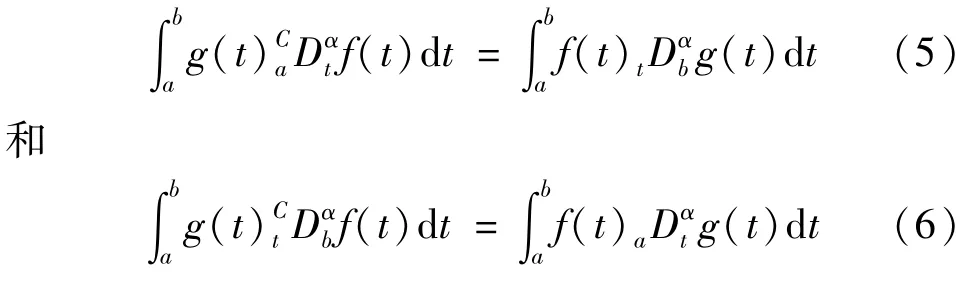
2 Caupto导数下分数阶Lagrange方程

设Hamilton作用量为：

其 中qs（s＝1，2，…，n） 为 广 义 坐 标，为系统的 Lagrange函数。

分数阶Hamilton原理可表示为：

带有交换关系：

由分数阶Hamilton原理可直接导出：

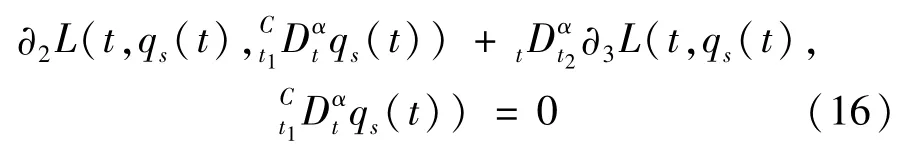
方程（16）就是Caputo导数下的分数阶Lagrange方程。由分数阶Lagrange方程描述的动力学系统可称为分数阶Lagrange系统。

3 特殊无限小变换下系统的Noether准对称性与守恒量

下面研究在时间不变的特殊无限小变换下分数阶Lagrange系统（16）的Noether准对称性与守恒量问题。首先由分数阶守恒量的Frederico-Torres定义[3]，我们有：

定义1对于分数阶Lagrange系统，当且仅当沿着方程（16）的所有解曲线，有：

其中，m是任意整数，对于每一组函数I1i和I2i（i＝1，2，…，m），满足

这里且，或且，则是该系统的分数阶守恒量。

定义2设L1是另外的一个Lagrange函数，则时间不变的特殊无限小变换

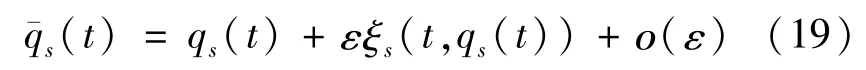
是分数阶Lagrange系统（16）的Noether准对称变换，当且仅当对任意[T1，T2]⊆[t1，t2]，有

成立。

由式（20），容易得到：

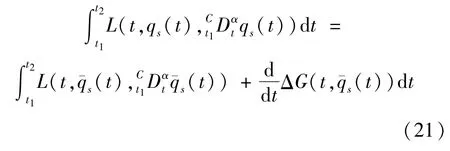
这里 ΔG＝εG（t，qs（t））。

判据1如果规范函数G（t，qs（t））和无限小生成元ξs满足条件：

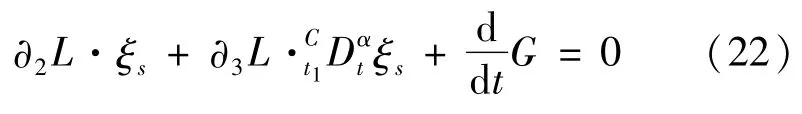
则变换（19）是分数阶 Lagrange系统（16）的Noether准对称变换。

证明考虑到式（21）对任意的积分区间[T1，T2]都成立，因此有：

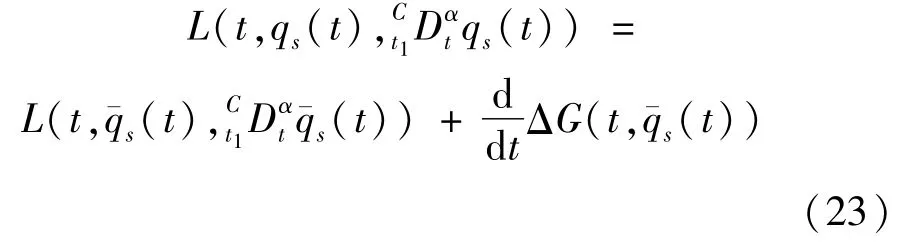
将式（23）对ε求导，并令ε＝0，可得：

定理1对于分数阶Lagrange系统（16），如果无限小变换（19）是其Noether准对称变换，则系统存在定义1意义下的分数阶守恒量，形如：

证明由方程（16）可得：

将方程（26）代入式（22），注意到式（8）和（9），我们有：

由定义1，即得结果。证毕。

定理1称为在时间不变的特殊无限小变换下分数阶 Lagrange系统（16）的 Noether准对称性定理。

4 一般无限小变换下系统的Noether准对称性与守恒量

下面研究在时间变化的一般无限小变换下分数阶Lagrange系统（16）的Noether准对称性与守恒量问题。

定义3设L1是另外一个Lagrange函数，则时间变化的一般无限小变换

是分数阶Lagrange系统（16）的Noether准对称变换，当且仅当对任意[T1，T2]⊆[t1，t2]，有

成立。

由式（28），我们有：

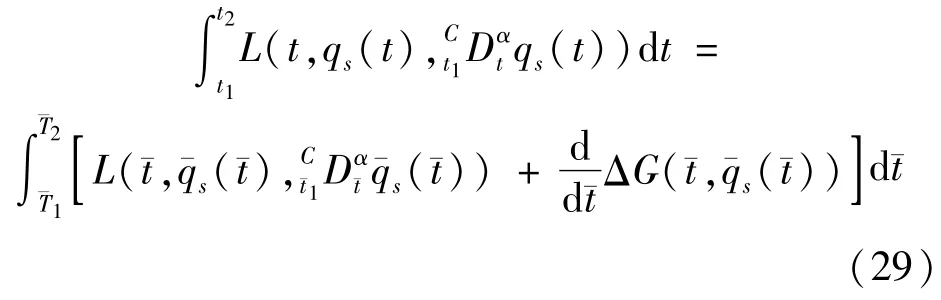
判据2如果规范函数G（t，qs（t））和无限小生成元和满足条件：

则变换（27）是分数阶 Lagrange系统（16）的Noether准对称变换。

证明由式（29），可得：

考虑到式（31）对任意的积分区间[T1，T2]都成立，因此有：

并注意到：

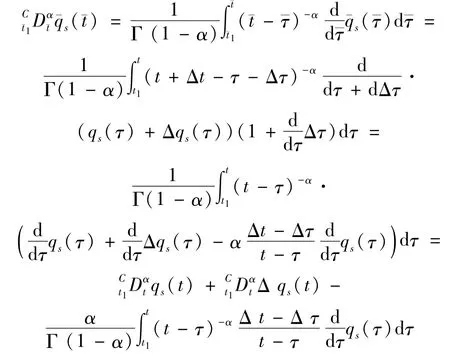
其中，Δt＝εξ0，Δqs（t）＝εξs。由于：

将式（33）代入方程（32），同时等号两边对ε求导，并令ε＝0，可得：

定理2对于分数阶Lagrange系统（16），如果无限小变换（27）是其Noether准对称变换，则系统存在定义1意义下的分数阶守恒量，形如：

证明引进李普希茨变换

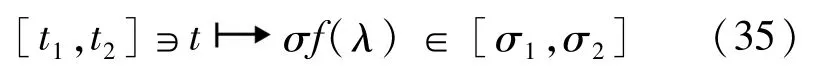
当 λ＝0时，满足则Hamilton作用量（12）可表示为：

因此，如果作用量S[qs（·）]在定义3意义下准不变，则作用量在定义 2意义下准不变。由定理1，表达式

是系统的一个分数阶守恒量。当λ＝0时，我们得到：

将式（41）和（42）代入式（39），得到：

定理2称为在时间变化的一般无限小变换下分数阶 Lagrange系统（16）的 Noether准对称性定理。

5 算 例

设力学系统的分数阶Lagrange函数

其中，ω为常数。

方程（16）给出：

由条件（30），我们得到：

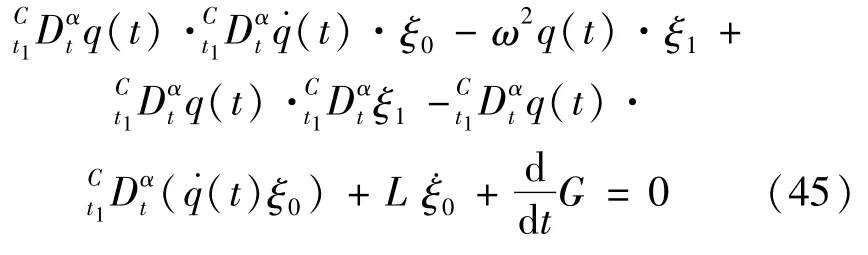
方程（45）有解：

生成元（46）相应于系统的Noether对称变换，生成元（47）相应于系统的Noether准对称变换。根据定理2，系统存在如下分数阶守恒量：

如取α＝1，则式（48）和（49）成为：

式（50）和（51）是经典Lagrange系统的能量积分。

6 结 论

基于分数阶微积分建立起来的非保守系统动力学模型可以更准确地刻划复杂系统的动力学行为。因此，近20年来分数阶约束力学系统动力学的研究引起了人们的广泛关注并取得了重要进展。本文主要工作如下：1）建立了Caputo导数下分数阶Lagrange方程。2）应用时间重参数方法研究了分数阶Lagrange系统的Noether准对称性，得到了Frederico-Torres形式的分数阶守恒量，建立了分数阶Lagrange系统的Noether准对称性定理。文中给出的方法和结果可望进一步推广应用于分数阶非完整力学系统等。

[1]RIEWE F.Nonconservative Lagrangian and Hamiltonian mechanics[J].Physical Review E，1996，53（2）：1890-1899.

[2]RIEWE F.Mechanics with fractional derivatives[J].Physical Review E，1997，55（3）：3581-3592.

[3]FREDERICO G SF，TORRESD F M.A formulation of Noether's theorem for fractional problems of the calculus of variations[J].Mathematical Analysis and Applications，2007，334（2）：834-846.

[4]FREDERICO GSF，TORRESDF M.Fractional optimal control in the sense of Caputo and the fractional Noether's theorem[J].International Mathematical Forum，2008，3（10）：479-493.

[5]FREDERICO G S F，TORRES D F M.Fractional Noether's theorem in the Riesz-Caputo sense[J].Applied Mathematics and Computation，2010，217（3）：1023-1033.

[6]FREDERICO G SF，TORRESD F M.Fractional isoperimetric Noether's theorem in the Riemann-Liouville sense[J].Reports on Mathematical Physics，2013，71（3）：291-304.

[7]ZHANG Y，ZHOU Y.Symmetries and conserved quantities for fractional action-like Pfaff variational problems[J].Nonlinear Dynamics，2013，73（1/2）：783-793.

[8]ZHOU Y，ZHANG Y.Noether's theorems of a fractional Birkhoffian system within Riemann-Liouville derivatives[J].Chinese Physics B，2014，23（12）：281-288.

[9]ZHANG Y，ZHAI X H.Noether symmetries and conserved quantities for fractional Birkhoffian systems[J].Nonlinear Dynamics，2015，81（1/2）：469-480.

[10]ZHAI X H，ZHANG Y.Noether symmetries and conserved quantities for fractional Birkhoffian systems with time delay[J].Communications in Nonlinear Science and Numerical Simulation，2016，36：81-97.

[11]张毅，周燕.基于Riesz导数的分数阶Birkhoff系统的Noether对称性与守恒量[J].北京大学学报（自然科学版），2016，52（4）：658-668.ZHOU Y，ZHANG Y.Noether symmetry and conserved quantity for fractional Birkhoffian systems in terms of Riesz derivatives[J].Acta Scientiarum Naturalium Universitatis Pekinensis，2016，52（4）：658-668.

[12]YAN B，ZHANG Y.Noether's theorem for fractional Birkhoffian systems of variable order[J].Acta Mechanica，2016，227（9）：2439-2449.

[13]SONG CJ，ZHANG Y.Conserved quantities and adiabatic invariants for fractional generalized Birkhoffian systems[J].International Journal of Non-Linear Mechanics，2017，90：32-38.

[14]何胜鑫，朱建青，张毅.基于分数阶模型的非保守系统的Noether准对称性[J].中山大学学报（自然科学版），2016，55（2）：58-63.HE SX，ZHU J Q，ZHANG Y.Noether quasi-symmetry for non-conservative systems based on fractional model[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2016，55（2）：58-63.

[15]何胜鑫，朱建青.基于分数阶模型的相空间中非保守力学系统的Noether准对称性[J].中山大学学报（自然科学版），2015，54（4）：37-42.HE SX，ZHU JQ.Noether quasi-symmetry for nonconservative mechanical system in phase space based on fractional models[J].Acta Scientiarum Scientiraum Naturalium Universitatis Sunyatseni，2015，54（4）：37-42.

[16]丁金凤，金世欣，张毅.基于Caputo导数下的含时滞的Hamilton系统的分数阶Noether理论[J].中山大学学报（自然科学版），2016，55（6）：79-85.DING J F，JING S X，ZHANG Y.Fractional Noether theorems for Hamilton system with time delay based on Caputo derivatives[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2016，55（6）：79-85.

[17]刘艳东，张毅.研究Noether准对称性定理的时间重新参数化方法[J].苏州科技大学学报（自然科学版），2017，34（2）：1-7.LIU Y D，ZHANG Y.The time-reparameterization method for study of Noether's quasi-symmetry theorems[J].Journal of Suzhou University of Science and Technology（Natural Science Edition），2017，34（2）：1-7.

[18]梅凤翔.经典约束力学系统对称性与守恒量研究进展[J].力学进展，2009，39（1）：37-43.MEI F X.Advances in the symmetries and conserved quantities of classical constrained systems[J].Advances in Mechanics，2009，39（1）：37-43.

[19]梅凤翔.约束力学系统的对称性与守恒量[M].北京：北京理工大学出版社，2004.MEI F X.Symmetries and conserved quantities of constrained mechanical systems[M].Beijing：Beijing Institute of Technology Press，2004.

[20]PONDLUBNY I.Fractional differential equations[M].San Diego：Academic Press，1999：62-77.

[21]KILBAS A A，SRIVASTAVA H M，TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterdam：Elsevier B V，2006：69-89.