通胀不确定下的最优消费、投资和自愿退休选择

陈雅豪,梅春晖,费为银

(安徽工程大学 数理学院，安徽 芜湖 241000)

最优消费投资问题是金融学研究的重要方向之一.1969年,Merton[1]就连续时间情形下最优投资选择问题进行了研究.随后,Merton[2]在1971年通过引入伊藤引理和随机动态规划的基本定理,发表了关于不确定性情形下最优连续时间动态模型的文章,并建立了经典的消费和投资模型.

此后,国内外学者扩展了Merton的研究.代理人用于基本生存需求的消费具有基本的意义,因为人只有维持生命的存在,才可能追求未来的发展.故在Merton经典的消费和投资模型基础上考虑加入生存消费等约束条件有现实意义.Gong和Li[3]在带有生存消费约束的动态消费和资产分配模型中,借助动态规划原理研究了通胀指数债券的作用,在CRRA效用函数下,推导出最优消费和投资的显示解,并且代理人投资于风险资产的意愿与风险偏好及股权溢价有关.

针对现在的金融问题,单单利用Merton模型已经无法较好地进行解释,于是一些学者逐步将现实因素以及市场的不确定因素考虑进来，比如考虑带有闲暇、劳动收入、退休选择等因素的最优消费投资问题研究.由于人们的平均寿命相比以前有了明显的增长,不言而喻,个体为自身退休而进行投资的需求就变得日益重要.Farhi[4]等在劳动闲暇框架下研究了最优消费、投资组合与退休选择问题,得到在提前退休情形下的投资者往往会增加储蓄并减少代理人的有效相对风险厌恶.Choi[5]等研究了一个无限寿命的代理人自愿退休的最优消费-闲暇及投资组合问题,利用对偶方法得到退休时的临界财富水平以及最优投资策略的闭型解.Lee[6]等研究了带有生存消费约束的最优消费、投资与自愿退休选择问题,运用动态规划方法得到了显式解.

然而,现如今通货膨胀已成为世界各国普遍存在的经济问题,面对其带来的压力,代理人考虑通货膨胀对消费投资的影响势在必行.国内外学者在通胀环境下对最优消费和投资选择问题也做出了大量研究.Brennan[7]等研究了通胀下动态投资组合最优化问题,运用鞅方法给出了最优投资策略的闭型解.Lim[8]研究了通胀风险和生存约束条件下的最优投资组合选择问题,定量分析了通胀风险和生存约束对最优策略的影响.费为银[9]等在递归效用的情形下,考虑投资者带通胀的最优消费和投资问题,利用动态规划的思想,获得了最优消费与投资策略.Kwak[10]等研究了通货膨胀风险下一个家庭连续时间内的最优消费、投资和人寿保险决策问题,分析了参数对最优策略的影响.

通过上述文献综合分析发现，研究者只是单单将实际问题如生存消费约束或退休选择考虑到最优消费和投资问题当中，或者只考虑了通货膨胀并没有将其结合起来,研究的创新在于将通胀因素、生存消费约束、通胀指数债券与退休选择结合起来,基于现有文献的基础上考虑通胀因素,对现有的模型进行进一步推广,利用动态规划方法得到消费和投资策略的闭型解.并进行数值模拟,分析通胀波动率对于代理人最优消费、投资选择的影响,给出合理的经济解释,使得模型更加符合实际.

1 基本模型

首先,假设市场中有三种金融资产:无风险债券,通胀指数债券和风险资产(股票),并且投资者必须选择投资在各种资产的金额.

式中，R是无风险债券的名义利率；μs是风险资产的平均回报；σs是风险资产收益的波动率；Zt是概率空间(Ω,F,P)上的标准布朗运动.

在许多情况下,通胀率的典型指标可以用CPI(消费价格指数)来表示,而消费价格指数可以视为一个价格水平过程如下:

式中，μp是预期通胀率；σp>0是波动率；Wt是不同于Zt的标准布朗运动.假定R、μp、μs、σp和σs为常数.因为存在两种不同的风险源,并且两种资产各包含一种风险,所以市场是完备的.在我们的金融模型中,投资者可以通过投资指数债券来对冲通胀风险.假设Wt和Zt的相关系数为ρ(-1<ρ<1),即d〈W,Z〉t=ρdt,那么存在一个与Zt互相独立的标准布朗运动Ut,且满足

{Ft}t≥0是由标准布朗运动{Zt,Ut}生成的自然流在概率测度P下的扩张.

通胀指数债券满足如下随机过程：

其中r表示真实利率.

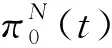
设Xt是代理人在时刻t的真实财富量,则实际财富过程由下列等式演变：

然后根据伊藤公式,得

(1)

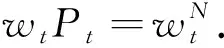
2 优化问题

现考虑代理人仅在退休前受到生存消费约束,以q>0表示一个退休前正的生存消费水平,代理人的目标是使消费的预期折现效用最大化,并有如下约束:ct≥q,对于所有0≤t≤τ.

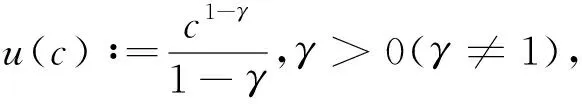
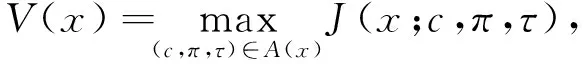
(2)

其中,

而δ>0是代理人的主观折现率,l>0是代理人的劳动负效用常量,U(·)是经典Merton问题的值函数,由下式给出：

其中K是Merton常数,定义为：

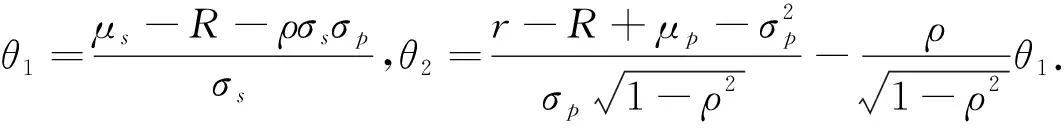
假设1 为了保证优化问题(2)有定义,作出如下标准的假定:K>0

3 模型的解

对于t<τ,值函数V(x)的HJB方程为

(3)

V(x)=U(x).

(4)

通过消费/投资组合过程的HJB方程(3)的一阶条件,有

c*=[V′(x)]-1/γ,

(5)

(6)

将式(5)与式(6)代入HJB方程(3)得

(7)

为了后文使用,定义两个二次代数方程如下:

(8)

(9)

其中f(α)有两个实根α1和α2满足α1>1>α2>0并且g(β)=0有两个实根β1和β2满足β1>0,β2<-1,并且两个代数方程根之间的关系如下：

采用文献[27]三氯化铁-铁氰化钾试剂法对20%vol和72%vol红枣白兰地的致浊物进行定性分析，实验结果，均呈现明显的蓝色斑点。表明致浊物中含有酚类物质，所得结果与红外吸收光谱相吻合。

(10)

定理1 优化问题(2)的值函数V(x)为

其中

(11)

(12)

与此同时,

(13)

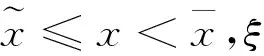
(14)

证明 相应的证明类似于参考文献[6]中定理4.2的证明方法.证毕.

定理2 最优策略(c*,π*,τ*)分别为

并且,

其中ξt是以下代数方程的解

证明根据HJB方程(3)的一阶条件、式(6),以及定理1中的值函数V(x),可以得出最优策略.另由式(14),可得代理人在时刻t的财富水平Xt.证毕.

4 数值模拟

为了更好地理解财富水平和通胀因素对投资者的最优消费和投资组合选择的影响,在本节中,结合定理2,在给定参数取值的基础上,通过Matlab软件进行数值模拟,具体分析如下.通胀波动率σp对最优投资π2的影响如图1所示.设定的参数为w=0.4,l=0.8,q=0.05.r=0.03,R=0.03,δ=0.07,μs=0.09,σs=0.2,μp=0.035.研究通胀波动率对最优投资的影响.

图1a与图1b表示代理人在最低生存消费的状态.图1a表示ρ为正数时的情形.由图1a可知，随着通胀波动率的增长,会刺激并活跃市场,代理人会借贷资金并且增加在风险资产上的投资;之后随着通胀波动率不断增大,市场环境恶化,代理人会放缓借贷投资的步伐,逐渐减少在风险资产上的投资.图1b表示ρ为负数时的情形.由图1b可知，随着通胀波动率的增长,因为此时不可预期风险资产收益与通胀风险之间呈现负相关,所以投资者会减少借贷,并减少在风险资产上的投资,为了缓解由于过高的通胀风险可能带来的损失.由于此段最优投资不受相对风险厌恶系数γ的影响，故图形中只有一条曲线.

图1c与图1d表示在退休之前的状态.图1c表示ρ为正数时的情形.由图1c可知，首先,当通胀波动率在可控范围附近变动时,一定程度上规避由于通货膨胀所带来的财富购买力下降的不利情况，代理人会增加在风险资产上的投资，然而当通胀波动率较大时,投资环境不确定性增强,从而投资在风险资产上的头寸慢慢减少,呈现出下降趋势.另外,对于图1c中3种不同的曲线,分别对应于相对风险厌恶系数为(γ=2,γ=3,γ=4),其它参数相同的情况下,当相对风险厌恶系数越大时,对于风险厌恶的投资者会减少风险资产上的头寸,这是理性的做法.图1d表示ρ为负数时的情形.由图1d可知，同样的从去趋势上看,随着通胀波动率的增长,经济代理人在风险资产上的投资迅速增加,之后随着通胀波动率的继续增大,代理人在风险资产的投资头寸不是趋于平缓了,而是以较快的速度减少.导致这种情况的原因是:一方面,还是因为通胀波动率的持续增大,会让投资者对金融市场表现出更多的担忧,从而会理性的做出投资决定——减少风险资产头寸;另一方面,因为此时不可预期风险资产收益与通胀风险之间呈现负相关,所以投资者会减少风险投资,为了减少由于过高的通胀风险带来的损失.在这两方面的作用下，因此当通胀波动率越来越大时,风险头寸减少的速度较正相关情况下更加迅速.

图1e与图1f表示在退休后的状态.图1e表示ρ为正数时的情形.由图1e可知，随着通胀波动率的增长,代理人会一直增加在风险资产上的投资,这是因为代理人退休后已经拥有足够的资金,并可以通过投资风险资产来获取一定的收益.当通胀波动率过大,投资环境恶化,从而代理人在风险资产上的头寸增加趋于平缓.图1f表示ρ为负数时的情形.由图1f可知，随着通胀波动率的增长,代理人会一直减少在风险资产上的投资,由于此时不可预期风险资产收益与通胀风险之间呈现负相关,另外加上退休后投资者的心理更希望拥有稳定的投资收益，更加不愿意去冒着风险进行投资,所以减少在风险资产上的头寸,转而投资收益较稳定的无风险资产.

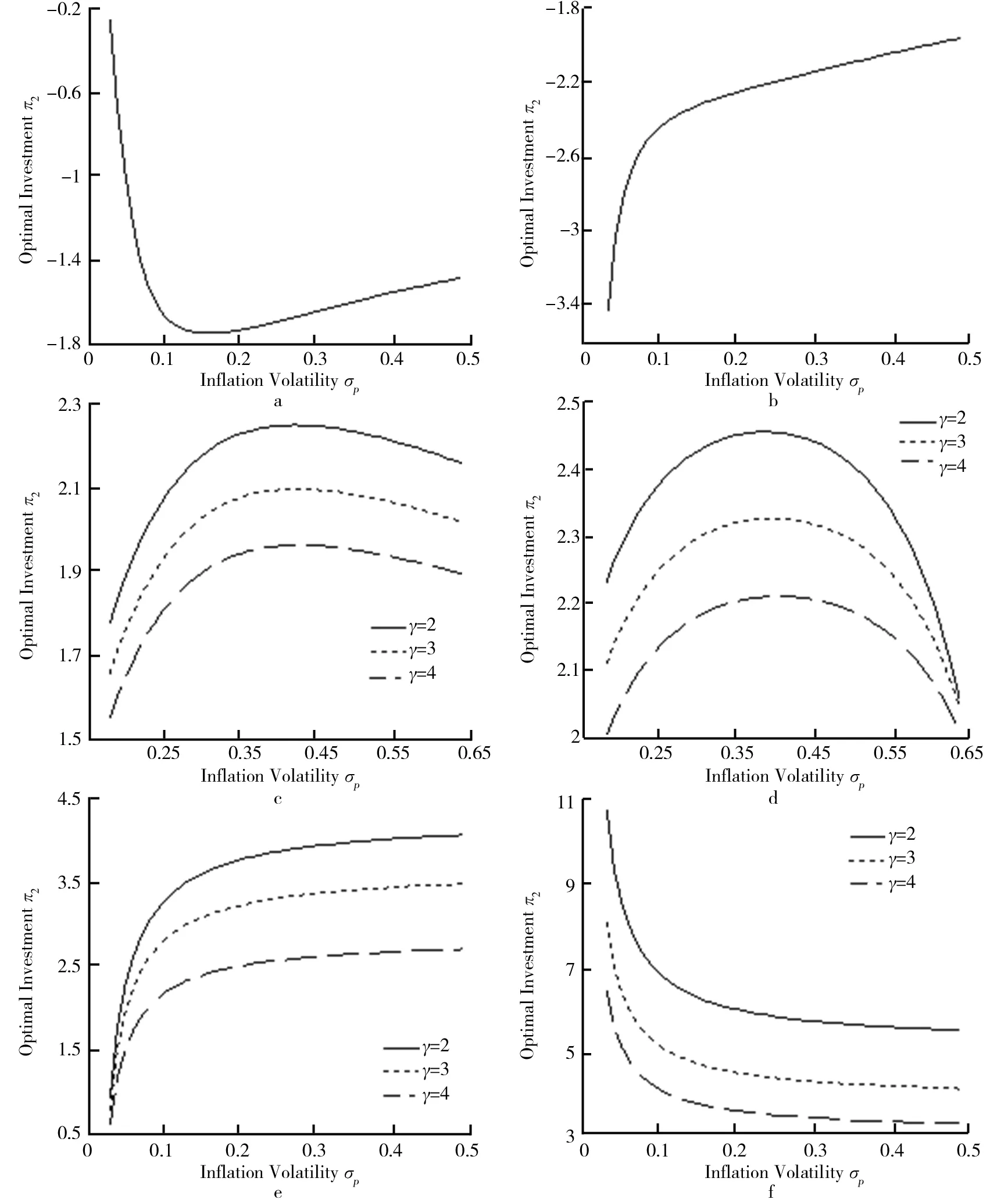
图1 通胀波动率σp对最优投资π2的影响

通胀波动率σp对最优消费Ct的影响如图2所示.在图2中,设定的参数为w=0.4,l=0.8,q=0.05.ρ=0.03,r=0.03,R=0.03,δ=0.07,μs=0.09,σs=0.2,μp=0.035.研究通胀波动率对最优消费的影响.在图2中若考虑相关系数ρ是负数,最优消费呈现出的趋势与正相关时一致.故这里给出相关系数是正数的情况.

图2a表示代理人在最低生存消费的状态,因为代理人一直维持着最低生存消费,所以消费水平一直不变.由于此段最优消费不受相对风险厌恶系数γ的影响,故图形中只有一条曲线.

图2b表示代理人在退休前的状态,结合图1c,通胀波动率在一开始的合理范围内,有着刺激投资的作用,那么代理人更加愿意把较多的资产投资在风险资产上进行增值保值;另一方面,从投资者心理上考虑,由于通胀的出现,导致货币购买力下降,这时会降低投资者的消费欲望,从而使得消费减少.之后当通胀波动率不断增大时,投资者的消费不会进一步减少,而是随着通胀波动率的增长，投资者对于这种因素带来的不确定性的承受能力渐渐提升,并不会因为一点点的波动就会很迅速地改变自己的决策,更有一种持观望态度在里面,缓慢增加消费渐渐的去适应当前的市场环境,以期能够在这种市场中做出更加正确的决策.另外,对于图2b中3种不同的曲线,分别对应于相对风险厌恶系数(γ=2,γ=3,γ=4).其他参数相同的情况下,这个阶段的投资者对于投资是很小心的,处于一种高风险厌恶的状态,所以当相对风险厌恶系数越大时,投资风险资产的头寸就会变少,相应的消费就会增多.

图2c表示代理人在退休后的状态.由图2c可知，一开始由于通胀波动率的增加,购买力下降,消费呈现下降趋势;随着通胀波动率的继续增加,消费呈现增加趋势,这是因为代理人对于购买力下降这种现象的承受能力也在持续增长,因此对消费的态度并不会像开始时那般抗拒,再者退休后代理人已经累积了足够的财富,从而有充足的资金用于消费.另外,对于图2c中3种不同的曲线,分别对应于相对风险厌恶系数(γ=2,γ=3,γ=4).风险厌恶系数越大,代理人更加不愿意把资产用于消费,因为通货膨胀最直观的影响就是货币贬值购买力下降,此时更加稳妥的办法是可以将资产用于无风险债券来保障最基本的收益以及防范未来的风险.

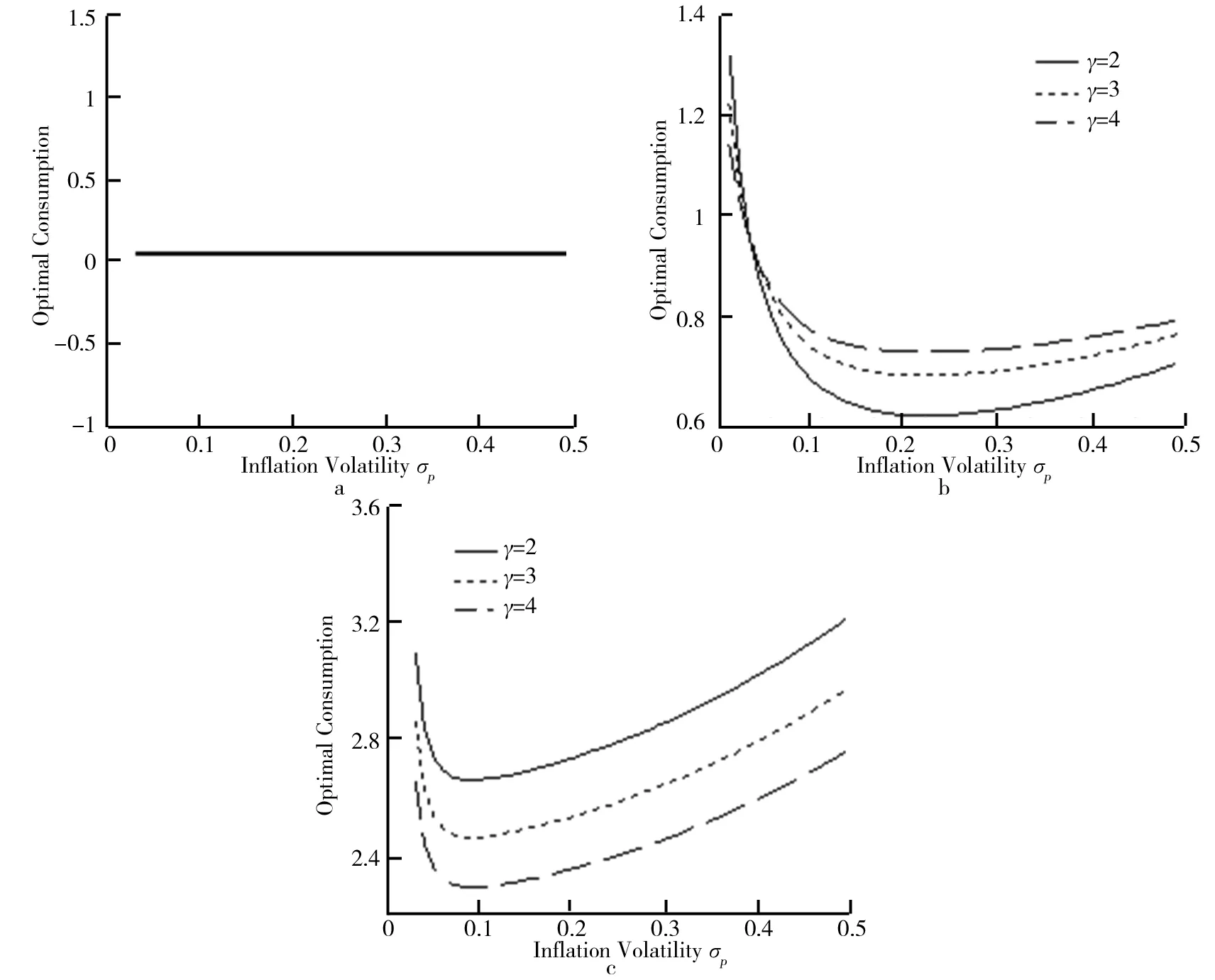
图2 通胀波动率σp对最优消费Ct的影响

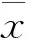
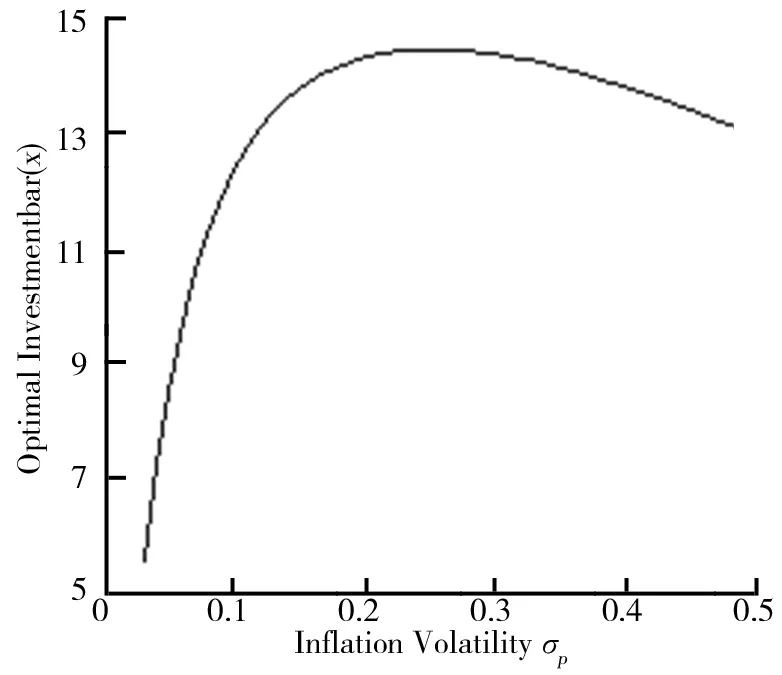
图3 通胀波动率对最优退休时间的影响

5 小结

将通胀因素、生存消费约束、通胀指数债券与退休选择结合起来,是一类具有理论与现实研究价值的投资组合问题.研究在通胀环境下建立模型,并利用随机分析推导真实环境下的财富过程,这更符合当前的金融市场,具有现实意义.借助动态规划方法和随机控制理论,得出了投资者的最优消费投资与退休策略.研究发现存在一个临界财富水平,当投资人的财富达到该临界水平时,选择退休.这在直观上也是很吸引人的,因为随着代理人的财富水平提高,闲暇较之收入更加重要.并且在研究最后通过数值分析分别考虑了通胀波动率和财富水平对经济代理人最优消费、投资的影响.结果表明,适当的通胀波动率有利于经济发展,使得投资者投资的积极性增强;然而随着通胀波动率持续增长,经济环境逐渐恶化,投资者对于投资风险资产会产生更多的担忧,不愿意继续进一步增加投资,反而会慢慢地减少投资来预防通胀风险可能带来的损失.因此,探讨通货膨胀环境下,代理人带有生存消费约束的最优消费、投资与退休决策具有一定的实际经济意义和理论价值,研究结果可以为投资者提供参考.

研究是在前人工作的基础上考虑通胀因素.在研究中考虑加入通胀指数债券对冲投资风险,更加贴近现实,具有现实的经济意义.另外,由于近年来在许多学者考虑通胀服从均值回复过程的最优投资组合策略问题，所以将原模型推广到到均值回复通胀环境中也是一个值得研究的方向.

[1] R C MERTON.Lifetime portfolio selection under uncertainty:the continuous-time case[J].The Review of Economics and Statistics,1969,51(3):247-257.

[2] R C MERTON.Optimum consumption and portfolio rules in a continuous-time model[J].Journal of Economic Theory,1971,3(4):373-413.

[3] N GONG,T LI.Role of index bonds in an optimal dynamic asset allocation model with real subsistence consumption[J].Applied Mathematics and Computation,2006,174(1):710-731.

[4] E FARHI,S PANAGEAS.Saving and investing for early retirement:a theoretical analysis[J].Journal of Financial Economics,2007,83(1):87-121.

[5] K J CHOI,G SHIM,Y H SHIN.Optimal portfolio, consumption-leisure and retirement choice problem with CES utility[J].Mathematical Finance,2008,18(3):445-472.

[6] H S LEE,Y H SHIN.An optimal consumption,investment and voluntary retirement choice problem with disutility and subsistence consumption constraints:a dynamic programming approach[J].Journal of Mathematical Analysis and Applications,2015,428(2):762-771.

[7] M J BRENNAN,Y XIA.Dynamic asset allocation under inflation[J].The Journal of Finance,2002,57(3):1 201-1 238.

[8] B H LIM.The effect of inflation risk and subsistence constraints on portfolio choice[J].Journal of the Korea Society for Industrial and Applied Mathematics,2013,17(2):115-128.

[9] 费为银,吕会影,余敏秀.通胀服从均值回复过程的最优消费和投资决策[J].系统工程学报,2014,29(6):791-798.

[10] M KWAK,B H LIM.Optimal portfolio selection with life insurance under inflation risk[J].Journal of Banking & Finance,2014,46:59-71.