数形结合在小学数学教学中的运用
2018-06-07史光龙
史光龙
(万年县石镇镇井路小学,江西上饶 335503)
一、趣味理解抽象概念
数的概念是学生认识和理解数学的开始,理解数的意义伴随学生学习数学的整个过程。帮助学生建立清晰的数的概念,理解数的意义。特别是越到高年段的学生遇到的数的概念越来越抽象,理解更加困难。画图与数的认识结合,能做到逐渐建立起抽象的数和现实中的数量之间的关系,同时让学生在这个理解的过程中体会和感受到数形结合的思想方法。
如,人教版五年级下册“分数再认识”,结合学生年龄段的认知特点,让学生从身边的实物找起。提出小组合作问题“可以表示什么?”,让学生举出生活中的例子,通过画图理解。让学生在小组里充分讨论交流,然后全班汇报交流:可以是表示把一个正方形平均分成4份,取其中的3份。也可以是把4个三角形平均分成4份,取其中的3份。画图表示还可以把12根骨头平均分成4份,取其中的3份让学生体会到的单位“1”可以是不同的整体,表示把不同的整体“1”平均分成4份,取其中的3份。而以前我们知道的分数的意义只是比较简单的整体“1”,现在丰富了对整体“1”的认识。从而引导学生概括出分数的意义“把一个整体平均分成若干份,取其中的一份或几份,可以用分数表示”。这个认识的过程,充分体现了举实例、画图理解分数的意义,尤其是理解整体“1”,尤其形象具体,容易理解。
二、运算方法更加便捷
《课标解读》中强调“应当淡化对运算的熟练程度的要求,选择正确的计算方法,准确地得到运算结果,比运算的熟练程度更重要。应当重视学生是否理解了运算的算理,是否能准确地得出运算的结果,而不是单纯地看运算的速度。”可以看出运算算理的重要性,而越是到了高年段数的运算算理的理解尤为重要,同时也尤为抽象。数与形结合,能将算理和算法有机结合在一起,从而提高学生的运算能力。
如,人教版六年级上册“分数除法”的教学,让学生理解分数除法意义时,问学生:“你能画图表示把一张纸的平均分成2份吗?求每份是这张纸的几分之几,怎样列式?”学生独立画图表示之后与同学交流画法,学生在交流中发现,分数除法的意义与整数除法的意义相同,都可以表示把一个数平均分。这个过程用画图,理解平均分成2份的过程,让学生感受数形结合的思想方法。教师接着问:“从你的画图中,能知道÷2的结果是多少吗?”学生观察后回答:“是。”教师又接着问:“那你能结合图来说说怎样理解这个算式的结果?”学生回答:“从图中可以知道表示4个,把4个平均分成2份,每份就是。计算过程可以写成”学生在老师的引导下思考问题越来越清晰了,初步感受了分数除法的计算方法。教师再追问:“像我们刚才这样利用图来理解分数除法的意义和算法,是个好办法,你们同意吗?那我们现在知道了分数除以整数(0除外),可以用分子除以整数,分母不变来计算,那是不是适用于所有的分数除法呢?”接下来就让学生继续探究“把一张纸的平均分成3份,每份是这张纸的几分之几?”这个问题。教师问:“那么这个问题,我们还会用画图的办法来理解吗?”有了第一个问题的基础,学生先独立画图,列式,观察,小组讨论交流。在学生遇到困难时,教师再在那个知识点上帮一把,让学生更加容易理解。教师问:“还能像刚才那样用分子除以整数,分母不变吗?为什么?”让学生感受到刚才那种方法是有局限性的,再引导他们从分数除法的意义来理解:“把一张纸的平均分成3份,利用图理解每份是3份中的一份,也就是求的是多少。”学生这时思维得到方向的引领,教师再接着问:“求的是多少,可以怎样计算?”进一步说:“把一张纸的平均分成3份,求每份就相当于求的是多少。”这时候学生有点恍然大悟了,很快知道
教师始终是引导者,学生才是学习的主动者。在潜移默化中渗透了数形结合的思想方法,让学生清楚算理与算法,同时也发展了学生的思维能力。
三、建立模型更加清晰
苏霍姆林斯基说:“在人的心灵深处有一种根深蒂固的需求,那就是希望自己是一个研究者、探索者、发现者,这种需要在儿童内心世界更为强烈。”而小学高年段学生好探究的天性更加强烈,如何让学生对抽象的数学知识探究起来不会太难,从而使探究更加有价值?特别是在小学高年段数学学习中,比较多的实际问题的解决,其中的数量关系,建立模型,使用数形结合的思想方法来分析,将会让学生的探究更加清晰。
如何让学生自己更好地理清数量之间的关系,学会解决分数乘法应用题,发展学生的思维能力?引导学生抓住关系句来理解数量之间的等量关系时,渗透数形结合的思想方法。题中的关系句“①摄影小组的人数是气象小组的,②航模小组的人数是摄影小组的”,为了使学生有一个清晰的分析,先让学生小组讨论交流几个问题:“(1)在①中是把什么看作了单位“1”?把什么平均分成了几份?谁有这样的几份?(2)在②中是把什么看作了单位“1”?把什么平均分成了几份?谁有这样的几份?”然后引导学生先画好线段图来理清其中的关系,最后全班交流:在①中是把气象小组看作了单位“1”,把气象小组平均分成3份,摄影小组有这样的1份,画成线段图表示是:
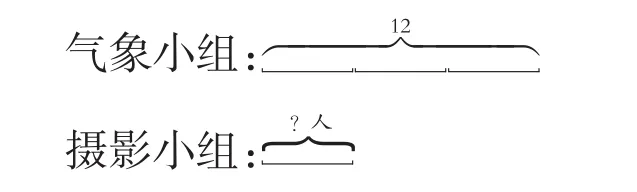
在②中是把摄影小组看作了单位“1”,把摄影小组平均分成4份,航模小组有这样的3份,画成线段图表示是:

引导学生找到数量之间的相等关系:根据单位“1”×分率=分率的对应量,可以知道“气象小组的人数×=摄影小组的人数,摄影小组的人数×=航模小组的人数”,从而得到解决方法。
在认识数,理解算理算法,理清实际问题中的数量关系,建立模型的过程中,学生经历、感受、体验了数形结合的思想方法,学会使用这种方法去理数的意义、关系。有了数形结合的思想方法,很多数学问题就可以迎韧而解了。这些数学方法不是教师告诉学生的,而是学生在探究的过程中自己体会和总结的,数学探究学习的过程就是数学方法运用并积累的过程。
