利用转化思想解决复合方程根的分布问题

安徽合肥师范学院数学与统计学院 洪 倩

安徽合肥一中 吴建平

近年来，有关复合方程根的分布问题经常出现在高考试题中，而大部分同学遇到这样的问题本能地存在恐惧心理，不知从何处入手，或者一部分同学知道从何处入手，却由于思维混乱导致分类、计算出现问题，从而使前一部分的努力付之东流。复合方程从本质上说就是把一个函数整体藏入另一个函数的自变量中，在解决复合方程根的分布问题中，最常用到的就是转化思想。转化思想在处理问题时，把待解决的问题，通过某种转化变为一类容易转化的常见问题。将复杂的复合方程转化成简单的一元二次方程进行求解，从而使得原问题巧妙解决。

我们来看以下这个例子：

例题：已知函数若关于x的方程f2（x）-有8个不等根，求a的取值范围。

分析：由于这道题涉及8个不等根，学生在解题过程中很容易无从下笔，一方面是因为不能很好地理解题意，另一方面未想到将复合方程转化成简单的一元二次方程。

解法1：在这里我们可以令 =t，即由图1知，要使+a=0这个方程有8个不等根，即要求在（1，2）内有两个不相等的根。

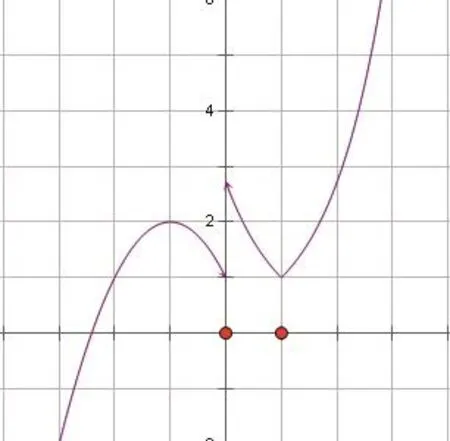
图1

则a要满足条件

得出

解法2：该方程在（1，2）内有两个不相等的根。

令在（1，2）上有2个交点，如图2，得出

图2

这道复合方程根的分布问题无论是从解法1还是从解法2去分析，都巧妙运用了转化思想，将复合方程转化成简单的一元二次方程，然后通过一元二次方程根的分布问题的一般解法进行解决。此类题目看似无从下手，实则简单，只要能够巧妙运用转化思想将其转化成常规题，即可以化难为易。转化思想就是要求我们换一个角度去处理问题，以使问题朝着有利于解决的方向不断变更，把同一问题用不同的形式在不同的水平上转化出来，转化就如同“翻译”，通过“翻译”，不仅使我们对能解决的问题不再停留在解决的层面上，而且让我们站得更高、看得更清、想得更好、表述得更简洁，做到既知道有几种解法，又明白以怎样的方向入手去解才是最简单的。

[1]俞观根.一元二次方程根的分布问题解法上的探究[J].黄山学院学报，2003（2）：80.

[2]范继荣.探究一元二次方程根的分布[J].教海探航，2011：39.

[3]杜素丽.浅谈转化思想在高中数学解题中的应用[J].学周刊，2014（7）：126.