变换问题角度，推动学生思维发展

江苏省南通市城南小学 何 艳

2011版《数学课程标准》明确指出“要促进学生解决问题的方法多样化”，在落实这一要求时，学生就会有更广阔的生长空间，可以从更多元的角度来展开探究，有所收获，并在学习过程中积累必要的经验，提升数学学习的层次。本文结合教学实践谈谈如何引导学生学会变换思维角度，具体可以从以下几个方面展开尝试：

一、学会问自己“为什么”

数学学习必须依托学生的领悟，在实际教学中，学生不能一味依靠模仿和记忆来学习，而是要主动探究，在不断地提出问题和解决问题过程中领悟数学知识。不仅如此，在数学学习中，我们还要引导学生有更高的追求，要让他们不仅满足于知道“是什么”，还要追求“为什么”，这样的刨根问底可以触及数学的本质规律。

例如在“按比例分配”的教学中，我给学生提供了这样两个问题：

（1）一个等腰三角形中有两个角的度数比是2∶5，那么三角形的顶角是多少度？

（2）一个等腰三角形的两条边的长度比是2∶5，其周长是36厘米，那么三角形的腰长多少厘米？

在学生独立尝试之后，我引导学生交流，第一个问题有很多学生没有想到两种可能性，在别的学生说出顶角的度数可能是2份也可能是5份后，学生发现果然如此。交流第二个问题时，原先只做了一种答案的学生从第一个问题中受到了“启发”，他们认为三条边的比可能是2∶5∶5，也可能是2∶2∶5，并根据这两种情况算出了三角形的底边长度。在学生一致认同这样的观点时，我故意停顿下来，用疑问的语气提示学生再想想，一会儿工夫，有学生反应过来，然后如星星之火般蔓延开来。此时我再指明学生说思路，学生就找到了问题的关键：三角形的两边之和要大于第三条边，所以不可能出现三条边的长度比是2∶2∶5的情况。

在小结这个环节时，不少学生的感悟是具体问题具体分析，说明经历了这样的学习过程之后，学生真正得到了启发，在今后的学习中，学生在分析问题时也许就能想得更深一点，不仅去探索怎么做，还会去问自己几个“为什么”，这对于推进学生的数学学习层次是有帮助的。

二、学会问自己“还可以怎么办”

数学知识之间是有着内在联系的，在数学学习中，很多时候我们不止有一种解决问题的途径，在教学中我们要帮助学生养成发散思维的意识，要让学生学会问自己“还可以怎样做”，当学生养成这样的好习惯之后，他们的数学学习就会更加灵动。

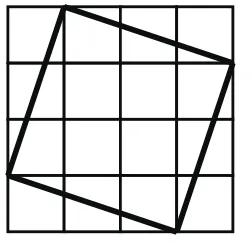
例如在“转化的策略”的教学中，我让学生思考如何求出图中（见右图）小正方形的面积。学生在独立思考之后展开了热烈的交流，展现了多种不同的思路：（1）用大正方形的面积减去四个三角形的面积。（2）在小正方形中将除了中间的4个正方形之外的部分两两组合成长方形，然后相加得到小正方形的面积。（3）数出正方形边上有4个点，内部有9个点，然后用4÷2＋9－1来计算（皮克定理）。在比较这些方法时，学生认为这些方法都是可以的，前两种方法的共同点是将三角形转化为长方形来计算，最后一种方法是将图形的面积转化为代数问题来计算。

我想学生之所以会出现这些不同的想法，与他们自己的高要求是分不开的，在面对问题时，很多学生已然具备了从不同角度来寻找不同的解决问题的方法的习惯，这就推动了方法的多样化，而方法的多样化必然带来方法的优化和深化。

三、学会问自己“一定要这样做吗”

如果要让学生能从不同的角度来看问题和思考问题，除了帮助他们养成意识和习惯之外，我们还可以从细节上来帮助他们，比如在学生成功地解决问题之后，我们要引导他们重新审视问题和解决问题的过程，问一问自己“一定要这样做吗”，很多时候，在这样的反思中会有新的发现。

例如在“长方体和正方体的体积”的教学中，我给学生提供了这样一个问题：一个长方体容器的长、宽、高分别是14分米、10分米和7分米，在容器中装有4分米高的水，现在用容器的右侧面作为底面，容器中的水深多少分米？在审题之后，学生抓住了容器中水的体积不变来解决问题：用14×10×4算出水的体积是560立方分米，再算出右侧面的面积是70平方分米，然后用560÷70算出水深8分米。在肯定学生的方法之后，我引导学生思考是不是一定要这样做，有学生从图中得到启发，发现原来的底面和现在的底面中有一条边是相同的，而这个长方体的长是高的两倍，说明原来的底面积是现在的两倍，所以现在的高必须是原来的两倍才能保持体积不变，由此学生发现了更简单的做法：14÷7×4＝8分米。这种方法无疑是智慧的，而学生之所以能有这样的发现，与教师的高要求是分不开的，与有意识地寻找不同方法的环节也是密不可分的。

总之，数学是一门灵动的学科，是最能锻炼学生的思维能力的，在实际教学中，我们要关注学生学习的细节，有意识地引导他们从不同的角度去展开思考，从而提升学生的学习高度，推动他们的思维发展。