双极性锌银电池电解液分配箱结构优化

余江洪，尹立兵，赵桦粮，詹志刚，3

(1.武汉船用电力推进装置研究所，湖北 武汉 430064； 2.武汉理工大学能源与动力工程学院，湖北 武汉 430070； 3.武汉理工大学材料复合新技术国家重点实验室，湖北 武汉 430070)

双极性锌氧化银贮备电池在比功率、比能量、可靠性和安全性方面的优点突出，在某些领域，如水下设备中，仍在广泛使用。近年来，人们对动力型锌银电池的比功率和比能量也提出了更高的要求[1]。多数电池组的失效是由于个别单体电池容量偏低所致，造成这种情况的一个主要原因是电池容量不均匀。电池容量不均匀，导致使用过程中容量偏低的电池组经常处于深充、深放状态，容量衰减较快。电池组的性能受容量较低的单体电池控制，因此单体电池的容量不均匀造成了电池组的失效。

宋二虎等[2]对锌银电池容量不均匀的问题进行了分析，对提高单体电池容量的均匀一致性的方法进行了探索，提出了改进途径，包括化学和结构方面的改进。R.A.J.Bajura等[3]从理论和实验两个方面验证了多分支液体分配系统的流动性，如压力分布、流阻等。H.T.Chou等[4]从实验和数值计算两个方面研究多口分布的管道，研究了二维的管道的沿程损失和动量损失。J.Y.Wang等[5]对等截面分支流结构的流量趋势进行了理论分析和试验研究，但只是从静态来分析液体的流动。刘志国等[6]利用流体动力学软件优化单体电池的内部结构，消除了局部涡流，改进了内部流场的均匀性。

本文作者以完整结构的电堆构建全尺寸几何模型，在电解液分配箱的入口施加随时间变化的实际的爆炸压力作为边界条件，以单体电池进液均匀性为优化目标，通过电解液灌注过程的全程动态模拟，对分配箱结构进行优化，以期获得最佳的电池性能。

1 模型及边界条件

1.1 几何模型

电堆完整结构及分配箱不同结构局部放大图见图1，总网格数为250万。

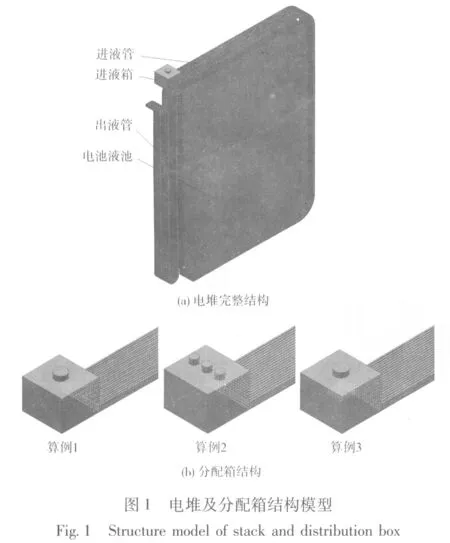
电池堆包括20只单体电池，电解液为KOH溶液，进入到分配箱之后，通过进液管分配到各单体电池。进入各单体电池的电解液量应尽量相同，电解液池中残留的空气量应尽可能少，以减少对活性区域的影响；同时，从出液管排出的电解液量应尽可能少，以提高利用率。为此，对分配箱的进口箱结构进行优化，出口尺寸为0.5 mm×2.5 mm×20 mm，不同结构算例及特点如表1所示。

表1 分配箱不同结构算例

1.2 数学模型

电池组激活时，电解液的灌注过程是KOH溶液进入电池框排出空气的过程，属于二相流的问题[7]。流体体积(VOF)模型具有追踪气液两相界面移动变化的功能，实验直接利用VOF模型来研究电解液灌注过程中气液运动。

灌注过程中没有考虑温度的变化，也没有发生相变，因此不解能量方程。VOF模型的传输方程分为3组。

质量守恒方程：

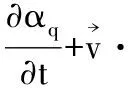
(1)

(2)

物理性能方程：

ρ=α2ρ2+(1-α2)ρ1

(3)

ρ=∑αqρq

(4)

动量守恒方程：

(5)

式(1)-(5)中：α为相体积分数；ρ为密度；v为相速度；g为加速度；F为各种力的综合；μ为黏度；下标q表示第q相。

1.3 边界条件

在进口箱施加(如图2所示)爆炸压力，大小随时间而变；仅考虑1 g的重力加速度。KOH溶液密度为1.35 g/cm3，工作温度为15～45 °C，黏度为2.5 mPa·s，与空气接触时的表面张力为0.8 N/m，与尼龙材质电解液池边框的接触角为51 °。

为研究分配箱电解液的流态及进入到各单体电池电解液的均匀性，利用流体动力学软件Fluent进行模拟计算。

2 结果及讨论

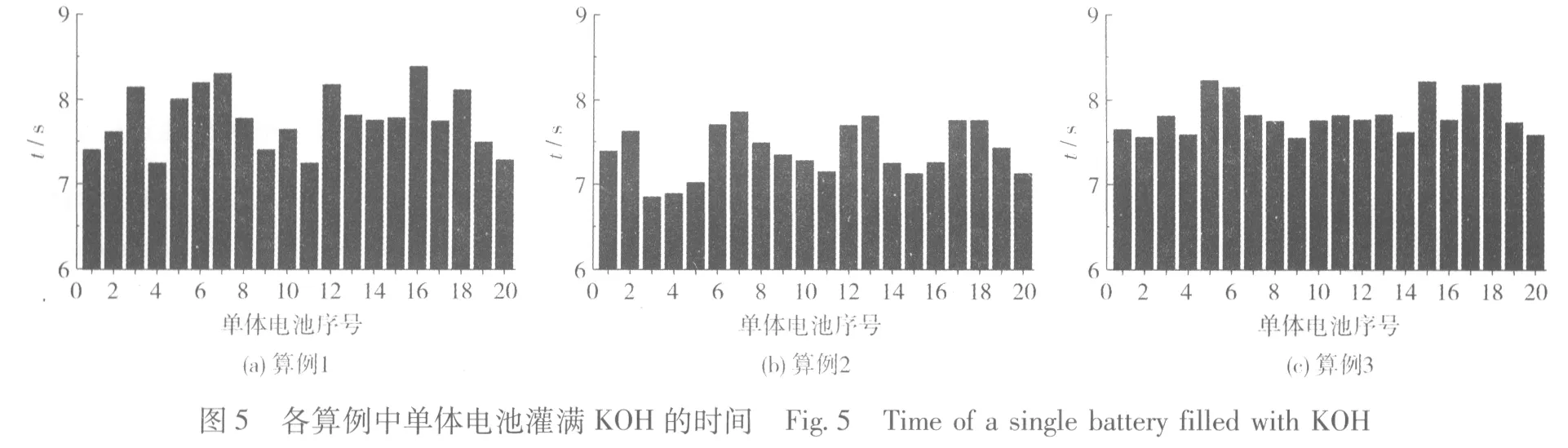
为考察不同进液箱结构的影响，选取灌注过程起始时刻、中间时刻及结束时刻电解液运动状态进行分析。以中间时刻为例，各算例分配箱KOH溶液体积分数的分布见图3，速度矢量的分布见图4。各单体电池灌满电解液所用的时间见图5。

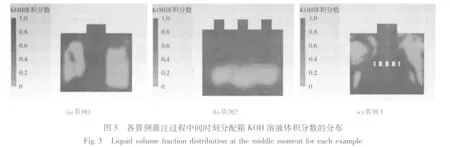
从图3可知，在算例1中，由于只有1个进液口，流体直接对着箱底部冲击，反弹之后形成向左及向右方向的漩涡，影响了箱底侧部进入到各单体电池的液体速度，进而影响各个单体电池电解液的分配量。在算例2中，进口分成3个小口，液体进入时有3股液流冲入底部，也形成小的漩涡，但总体而言，速度分布比算例1要均匀。在算例3中，因为进口下部有一个多孔的挡板，可以缓冲进入的液体的冲击，使进口箱液体的不均匀性移动到挡板之上，挡板下和单体电池进口连接的部分较均匀，可对流体产生一个再次分配的均匀化作用，因此速度矢量中的漩涡较小，进入到各个单体电池的液体量就比较均匀了。

每只单体电池的容量是相同的，如果要将灌注较慢的单体电池也灌满电解液，那么已经灌满了的单体电池就会溢出电解液，产生浪费，电解液的溢出量应该尽量少。从图5(a)可知，进液口直接对着的单体电池，速度较快，灌注时间短；左右两侧漩涡下的单体电池需要较长时间，而两侧面上由于受壁面限制，动压头转换为静压头，速度也较快，灌注时间也较短。从图4可知，单体电池灌注时间和速度矢量分布基本一致。与此类似，图5(b)中，3个进口直对着单体电池的进液速度也较快，用时较短，而漩涡下的单体电池进液速度较慢，所用时间较长；总体来看，电堆进液不均匀性稍有提高。图5(c)中，因进口下方多孔挡板的作用，电堆单体电池电解液灌注时间比较均匀，整体均匀性最好。

几种算例结果汇总见表2。

表2灌注时间、单体不均匀度以及残留空气量比较

Table 2Comparisonoffillingtime，uniformityandresidualairofsinglebatteryforeachexample

算例灌满电池组平均时间/s单体电池之间不均匀度1)/%电池内残留空气量/%结论17.8121单池灌注不均匀较高27.5111单池灌注不均匀较高38.571满足要求,挡板设置稍复杂

1)：单体电池最先与最后灌满的时间差与最后灌满的时间值之比

从表2可知，电解液灌注总体平均时间相差不多，但单体电池之间的不均匀度以第3种结构最好，电池内残余空气量也相差不大。由此可见，在进口箱增加多孔挡板结构后，电解液灌注效果最佳，灌注时间、单体电池灌注不均匀性和电池内残余空气等指标已达到要求。

中间挡板的开孔孔径、孔数及分布对灌注效果会有较大的影响。如果开孔率相同，孔径较小但孔数较多，单体电池不均匀度较好；主进口正下方孔分布较稀而向外围逐渐较密，单体电池不均匀度较好，但是可能导致进口压力增加。尽管增加挡板会使制造工艺变得复杂，导致成本增加，但可以提高电池堆的性能及可靠性。该结构已能满足研发要求，鉴于计算量巨大，实验未对挡板开孔及分布特性进行进一步的优化。

3 结论

本文作者针对完整结构的电堆，构建几何模型，以实际爆炸压力作为边界条件施加于分配箱入口，基于流体动力学方法，对分配箱结构进行优化，以期获得单体电池电解液灌注量的均匀分配，进而获得最佳的电池性能。在进口箱入口下部增加多孔挡板的结构，电解液灌注时间、单体电池灌注不均匀性、电池内残余空气等指标分别达到8.5 s、7%和1%，均满足要求。