固体氧化物燃料电池建模及广义预测控制
2018-06-06李俊红沈文兵宗天成
李 肖,李俊红,沈文兵,宗天成
(南通大学电气工程学院,江苏 南通 226019)
为使固体氧化物燃料电池(SOFC)可靠、稳定和高效地工作,需要确定系统的动态输入-输出特性[1]。谭勋琼等[2]基于内部气体流量的动态守恒方程,推导在假设条件下各种气体分压和电流的函数关系,进而构建SOFC的集总模型。阙加雄等[3]基于SOFC内部的3种动力学过程,综合考虑内部的质量平衡、能量平衡和电化学反应过程,建立动态模型。SOFC的内部反应复杂,且模型具有随机干扰、非线性等特点,因此建立的模型都很复杂,难以用于控制系统的分析和设计[4]。系统辨识方法是利用系统的输入-输出数据来确定系统的数学模型,更适用于工程应用[5]。
广义预测控制算法采用反馈校正和滚动优化策略,具有较强的鲁棒性,适用于复杂的工业过程控制[6]。本文作者通过SIMULINK搭建燃料电池的机理模型,分析并获得模型的输入-输出数据,再辨识SOFC的数学模型,避开电池的复杂反应过程来建模,并进行广义预测控制算法的设计。
1 SOFC机理建模
燃料电池模型电压包括4种电压:开环电压(En)、活化极化损失电压(Ua)、浓度损失电压(Uc)和欧姆损耗电压(Uo)。SOFC工作电压(Ud)按式(1)计算:
Ud=En-Ua-Uc-Uo
(1)
本文作者使用MATLAB/SIMULINK软件实现SOFC机理模型的实现,设计的基于SIMULINK的SOFC模型见图1。
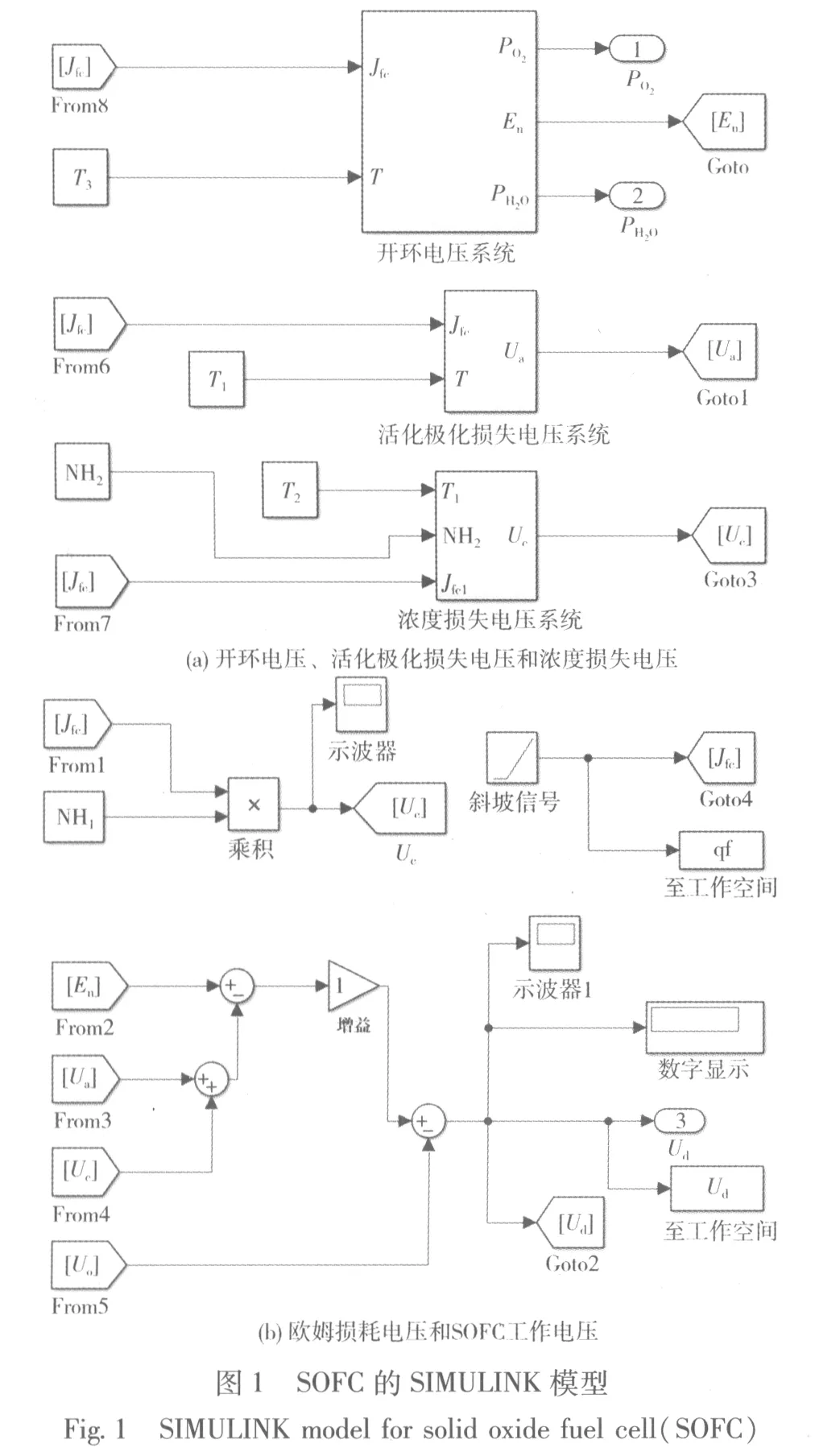
图1中:Goto模块用于保存端口的输出;From模块用于将保存的端口输出送入指定模块;Jfc是电流密度;qf是获取的电流数据;T、T1、T2和T3均是工作温度,取值为973 K;NH1是内阻,取值为0.126 Ω;NH2是输入流速,取值为51 ml/s。
2 SOFC电池的模型辨识
系统辨识是根据动态系统的输入-输出数据构造数学模型的过程[5]。在理论建模太复杂的时候,经常采用系统辨识的方法。为满足控制系统设计的需要,利用MATLAB中的系统辨识工具箱,辨识SOFC的输出电压响应模型,从而可避开SOFC内部复杂的反应机理。
将系统的输入-输出数据导入系统辨识工具箱,经过对各种模型结构辨识结果的分析与对比,最终选择具有外部输入的自回归滑动平均(ARMAX)模型作为SOFC的模型结构。通过系统辨识工具箱辨识出的系统具体参数为:
A(q-1)=1-1.22q-1+0.22q-2
(2)
B(q-1)=0.99
(3)
C(q-1)=1+0.927q-1
(4)
式(2)-(4)中:q-1为时延因子;A(q-1)、B(q-1)和C(q-1)均是q-1的多项式,为系统参数。
3 SOFC的控制设计
3.1 广义预测控制算法简介
广义预测控制(GPC)算法结合了多种算法的优点[6],如果能加以应用,可提高SOFC系统的控制效果。
3.2 预测模型
GPC采用式(5)作为系统的预测模型
A(q-1)y(k)=B(q-1)u(k)+C(q-1)ξ(k)/δ
(5)
式(5)中:δ为差分算子,δ=1-q-1;k表示采样时刻序列;y(k)、u(k)是系统的输出、输入;ξ(k)是均值为零的白噪声序列。
为了进行柔化控制,控制的目标是跟踪如式(6)所示的参考轨线。
w(k+j)=ajy(k)+(1-aj)yr(j=1,2,…,n)
(6)
式(6)中:j为预测长度;w(k+j)为系统的超前j步参考轨线;y(k)和yr分别为输出值和设定值;α为柔化系数,0<α<1。
根据预测控制理论,引入Diophantine方程可得到:
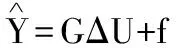
(7)
(8)
(9)
ΔU=[Δu(k),Δu(k+1),…,Δu(k+n-1)]T
(10)
f=[f(k+1),f(k+2),…,f(k+n)]T
(11)
3.3 最优控制律
若令W=[w(k+1),w(k+2),…,w(k+n)]T,则目标函数J可写成:
J=(Y-W)T(Y-W)+λΔUTΔU
(12)
式(12)中:Y是输出矩阵。

ΔU=(GTG+λI)-1GT(W-f)
(13)
如式(13)所示,在控制量加权系数λ和柔化后的设定值向量W均已知的情况下,若求ΔU必须先知道G和f。由式(7)可得:
y(k+n)=gn-1Δu(k)+…+g0Δu(k+n-1)
+f(k+n)+Enξ(k+n)
(14)
令X(k)=[Δu(k),Δu(k+1),…,Δu(k+n-1),1],θ(k)=[gn-1,gn-2,…,g0,f(k+n)]T,输出预测值可写成:
y(k+n/k)=X(k)θ(k)
(15)
式(15)中:X(k)为信息向量;θ(k)为待估计参数向量。
θ(k)可用最小二乘法估计得到:
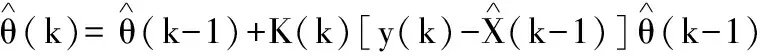
(16)
(17)
(18)
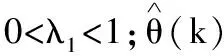
预测向量f可由式(19)得出:
(19)
在求得G和f后,可计算控制量ΔU的值,从而计算预测输出值。
3.4 比例积分微分控制算法
比例积分微分(PID)控制器是发展最早的控制方法之一,涉及的算法设计和结构都很简单,且适用于工程应用。目前,PID控制凭借简单易懂、适应性强等优势,仍然在实际生产中获得广泛应用。PID控制器根据给定值与实际输出值构成控制偏差e(t),偏差e(t)与控制量u(t)的关系为:
(20)
式(20)中:Kp为比例系数;Ti为积分时间常数;Td为微分时间常数。
3.5 仿真研究与分析
在对SOFC建模时,选择ARMAX模型为最终辨识结果,参数可由系统辨识工具箱获得。ARMAX模型的形式为:
A(q-1)y(t)=B(q-1)u(t)+C(q-1)e(t)
(21)
将式(2)、(3)和(4)辨识出的参数A(q-1)、B(q-1)和C(q-1)代入ARMAX模型的一般形式,整理得到:
y(t)=1.22y(t-1)-0.22y(t-2)+0.99u(t)
+e(t)+0.927e(t-1)
(22)
辨识出的模型采用广义预测控制算法,通过控制氧气的流量,研究在外部负载(电流)突然增大或减小时,电池输出电压的跟踪性能。选取设计参数:模型长度p=6,预测时域长度n=6,控制时域长度m=2,控制加权系数λ=0.7,柔化系数α=0.5;最小二乘法参数初始值为:gn-1=1,f(k+n)=1,其余为0,广义预测控制效果如图2(a)所示;针对SOFC模型,设计PID控制器,控制效果见图2(b)。
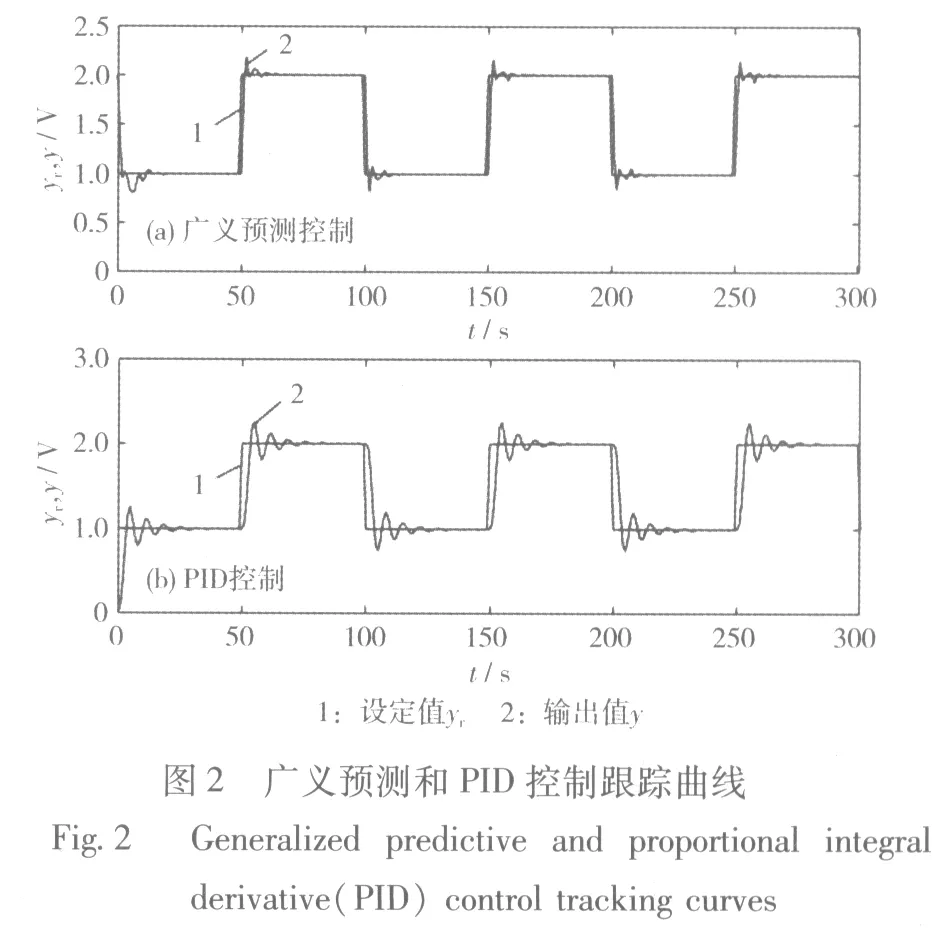
从图2可知,当系统的设定值发生变化时,两种算法经过一段时间调节之后,均能达到稳定值,但广义预测控制算法的调节时间更短,大约为12 s,最大超调量大约为7%,而在PID控制算法下,输出曲线经过约31 s达到稳定值,最大超调量大约为11%,因此广义预测控制算法跟踪给定值的控制效果较好,超调量更小,系统的响应速度更快。与PID控制相比,广义预测控制算法具有更好的跟踪性能。
4 总结
本文作者分析了SOFC的反应机理,建立了SOFC的物理模型,从而获得电池模型的输入-输出数据。根据这些数据,再用MATLAB中的系统辨识工具箱辨识SOFC的ARMAX模型。利用系统辨识避开了电池内部复杂的反应机理,使用价值很高。根据辨识得到的ARMAX模型设计广义预测控制算法,并与经典的PID控制对比。结果表明:当电池的负载发生扰动时,广义预测控制算法具有更好的跟踪效果。
