两阶段Logit广义估计方程的渐近性质

陈显彬,林 松,尹长明

(广西大学 数学与信息科学学院， 南宁 530004)

1 背景和主要结果

广义估计方程是对纵向数据进行回归分析的一类重要方法，由Liang等[1]于1986年对广义线性模型推广而得到。1983年，McCullagh等[2]出版了专著来系统地论述广义线性模型。对于自然联系函数的情况，极大似然估计的弱相合性和渐近正态性的条件在文献[3-5]中都有列出。特别关于Logit模型的条件，文献[6-8]也给出了论述。对于非自然联系函数，文献[9]给出了相应的渐近结果，但没有严格的假设和条件，而文献[10]则需要非常强的条件。由于之前研究存在一定的局限性，1985年L.Fahrmeir和H.Kaufmann发表了文献[11]，论述了极大似然估计的渐近性质；1986年，两人在文献[12]中具体分析了离散相应变量的渐近推断，又丰富了广义线性模型的相关理论。

本文设在试验中对第i个个体的第j次观测得到q×1维响应变量Yij，pn×q维协变量Xij，i=1,…,n,j=1,…,m。设来自不同个体的观测值相互独立，来自相同个体观测值则是相关的，但相关系数未知。令Yij=(Yij1,…,Yijq)T的期望为

(1)

(2)

方差记为

(3)

(4)

若Yij服从三项分布(观测次数是1)，即q=2,期望

(5)

(6)

就得到两步Logit模型[13-14]。

Wang[15]在一定条件下证明了经典Logit广义估计方程

(7)

对两阶段Logit模型，假设以下条件成立：

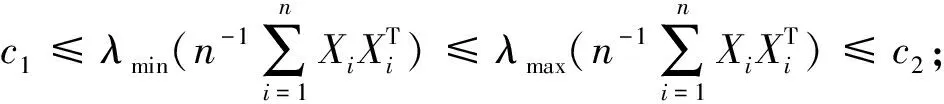
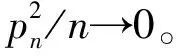
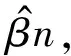
(8)

2 定理1的证明

为了证明定理1，需要以下引理：

下面4个引理的证明分别与文献[4]引理3.1、3.3、3.4、3.5类似，故在此省略。

引理2 若假设条件①～⑤成立，则

引理3 若假设条件①～⑤成立，则∀Δ>0，an,bn∈Rpn，有

引理4 若假设条件①～⑤成立，则∀Δ>0，an,bn∈Rpn，有

引理5 若假设条件①～⑤成立，则∀Δ>0，an,bn∈Rpn，有

定理1的证明

根据引理1，证明方程Sn(βn)=0根的存在性且式(8)成立，只需证明∀ε>0，存在一个Δ>0，对足够大的n有如下式子成立：

(9)

由微分中值定理,

(10)

(11)

(12)

其中εi(βn)=Yi-hi(βn)。所以

(13)

由引理2和假设⑤得

(14)

(15)

由引理3和假设⑤得:

(16)

(17)

由引理4和引理5及假设⑤得：

(18)

由假设②～④可得

(19)

由式(16)～(19)知In2≤-CΔ2pn，再由式(13)和(14)知|In1|=ΔOp(pn)，可见当Δ足够大时式(8)(9)成立。

[1] LIANG K Y,ZEGER S L.Longitudinal data analysis using generalized linear models[J].Biometrika,1986,73:12-22.

[2] MCCULLAGH P,NELDER J A.Generalized Linear Moders[M].New York:Chapman&Hall,1989.

[3] HABERMAN S J.Maximum likelihood estimates in exponential response models[J].The Annals of Statistics,1977,66:815-841.

[4] ANDERSEN E B.Discrete Statistical Models with Social Science Applications[J].North Holland,Amsterdam,1980(3).

[5] NORDBERG L.Asymptotic normality of maximum likelihood estimators base on independent,unequally distributed observations in exponential family models[J].Scandinavian Journal of Statistics,1980:27-32.

[6] HABERMAN S J.The Analysis of Frequency Data Univ[M].Chicago:Chicago Press,1974.

[7] MCFADDEN D.Conditional logit analysis of qualitative choice behavior[M].Academic,New York:[s.n.],1974.

[8] GOURIEROUX C,MONFORT A.Asymptotic properties of the maximum likelihood estimator in dichotomous logit models[J].Econometrics,1981(2):83-97.

[9] MATHIEU J R.Tests ofχ2in the generalized linear model[J].Statistics:A Journal of Theoretical and Applied Statistics,1981(3):509-527.

[10] FAHRMEIR L,KAUFMANN H.Consistency and asymptotic normality of the maximum likelihood estimator in generalized linear models[J].The Annals of Statistics,1985(3):342-368.

[11] FAHRMEIR L,KAUFMANN H.Asymptotic inference in discrete response models[J].Statistische Hefte,1986(4):179-205.

[12] FAHRMEIR L,TUTZ G.Multivariate statistical modelling based on generalized linear models[M].New York:Springer-Verlag,1994.

[13] MORAWITZ B,TUTZ G.Alternative parametrizations in business tendency surveys[J].Zeitschrift Operations Research,1990,34:143-156.

[14] WANG L.GEE analysis of clustered binary data with diverging number of covariates[J].Annals of Statistics,2011,39(1):389-417.

[15] ORTEGA J M,RHEINBOLDT W C.Iterative solution of nonlinear equations in several variables[M].San diego:Academic press,1970.