动态区间标度下的群组序关系评价法及其应用
2018-06-06肖文星
肖文星,杜 纲
(天津大学 管理与经济学部, 天津 300072)
当在传统的静态综合评价中引入时间因子,便构成了动态综合评价。动态综合评价作为综合评价理论的一个重要组成部分,目前在社会、经济、军事及管理活动中已得到了广泛的应用[1-6],并且取得了许多阶段性的研究成果[7-10]。在求解动态综合评价问题时常常需要利用属性的权重信息来实现方案的排序与择优,因此在解决这一类问题之前如何确定属性的权重显得尤为关键。由于不确定型多属性动态综合评价问题存在多信息、多偏好、动态不确定的复杂特征,目前相关的研究成果还很零散[11-17],因此针对属性权重未知的动态综合评价问题进行研究并提出一套科学合理的理论评价模型十分必要。
文献[17]针对属性权重不确定的静态综合评价问题首次提出了一种区间标度群组序关系评价法。这是一种考虑了区间数及群组判断的主观赋权法,该方法相比与其他传统主观赋权法(特征值法)虽具有简便、直观、易计算的特点,但它与其他传统主观算法一样仅仅局限于处理静态数据,若直接应用于动态评价问题中则无法兼顾不同时期属性值所体现的价值差异,权重分配也不够合理。鉴于此,本文针对属性权重不确定的动态综合评价问题进行了分析研究,提出了一种新的动态区间标度下的群组序关系评价法。本文研究的工作主要体现在以下两点:一是考虑了动态区间标度情形;二是考虑了群体判断不完全一致的情形。算例的验证结果表明这套模型具有计算简便、思路清晰、应用范围更广、更贴近实际的良好特性。
1 原理与方法
对于一个动态综合评价问题,设被评价对象集O={o1,o2,…,on},评价属性(指标)集为X={x1,x2,…,xm},设xij(tk)表示第i(i=1,2,…,n)个被评价对象在第tk(k=1,2,…,T)时刻关于属性xj(j=1,2,…,m)的观测值,S={s1,s2,…,sL}表示专家集。为研究需要,本文假设经全序列法[18]动态量纲为一处理后的规范化时序立体数据表如表1所示(全序列法的相关定义及性质参见文献[18]),表中的数据类型为实数型。

表1 时序立体数据

由于上述问题存在多属性、多偏好、多阶段及不确定的复杂特征,需要构建一个全面、合理的理论评价模型进行求解。鉴于此,本文首先对区间标度群组序关系评价法原理做一个简单描述,然后根据新的研究情境拓展出一种新的动态区间标度群组序关系评价方法。
1.1 区间标度群组序关系评价法原理
区间标度群组序关系评价法的算法步骤主要分为如下5步:
步骤1 依据理性赋值参考表给出属性重要性比值的理性赋值区间rk(k=2,3,…,m)。
步骤2 属性区间权重计算定理,得出每位专家sl(l=1,2,…,L)判断下属性的区间权重。
步骤3 确定各属性权重的群体协商区间Wk,并用群体协商点模型得出相应的群体协商点τk。
步骤4 建立并求解规划模型,计算出各指标xk(k=1,2,…,m)权重协商系数,最后求得各属性的权重点值。
步骤5 根据建立并求解线性集结模型,得出各被评价对象oi(i=1,2,…,n)的静态综合评价值并排序。
这里只是对区间标度群组序关系评价法原理进行了一个简单的叙述,关于上述各名词的具体定义、性质及模型的详细步骤原理可参见文献[17]及其他相关文献,在此不再赘述。
1.2 动态区间标度下的群组序关系评价法原理

1) 虽然来自同一领域部分专家对同一问题的理性认识大体相同,但事实上,由于个体偏好、知识结构和经验的不同,并非所有的专家给出的属性间定性序关系可以保持完全一致,因此假设在所有专家群体中存在L0(1≤L0≤L)位专家给出了与其他L-L0位专家不一致的属性间定性序关系是比较符合实际的。


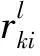
(1)

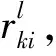

表2 理性赋值时序立体数据
(2)
为专家sl给出的属性xk权重比值判断的动态偏好区间。
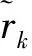
(3)


在此,本文针对上述假设分别建立了两种权重集结模型并集成求得属性的动态权重,权重以“综合”点值的形式给出。
1)L0位专家群体判断序关系一致情形
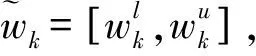
(4)


一般而言M≠∅,因为来自同一领域的L位专家对于同一问题的理性定性判断大体上是相同的[1]。
定义5 对于属性xk的权重一致区间,称映射
(5)
(6)
2)L-L0个专家群体判断序关系不一致情形

(7)
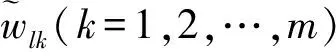

(8)
(9)

(10)
对自变量wj,β分别求偏导并令偏导数为0,求得
(11)
j=k=1,2,…,m
(12)
最后还需要建立一个将属性值与属性权重有效集结的规划模型以便得到方案的动态综合评价结果并排序。同样为不失一般性,在此采用简单的线性动态规划模型进行集结:
(13)
其中:yi(i=1,2,…,n)表示第i个被评价对象(方案)oi的动态综合评价值;xj(tk)表示方案oi对应的属性xj在tk时刻的观测值;wj表示属性xj权重值。
为了更清晰地描述动态区间标度下的群组序关系评价法,本文对上述进行了总结并给出了以下算法步骤:



步骤4 针对两种群体判断序关系情形,依据定义3-定义6、式(4)-(7)、式(8)-(11)分别建立属性权重一致性模型及单目标最优化模型,求得属性动态主观权重。

步骤6 根据式(13)计算得到每个被评价对象(方案)oi的动态综合评价值yi(i=1,2,…,n),并进行排序择优。
2 实例
本文通过一个实例说明方法的有效性与优越性,数据引自文献[20]中的实例。某大型服装公司,需要对几家供应商进行综合评估并从中选出最合适的供应商作为合作伙伴。现在有4家供应商O=(o1,o2,o3,o4)参与评估。企业对每个供应商从2007—2012年6年的发展变化进行综合评定,现假设对应的属性集X=(x1,x2,x3,x4,x5),分别表示成本、质量、交货期、服务水平及未来发展潜力。其中,x1、x3为成本属性,其余的属性为效益属性,且x2、x4、x5为定性属性,专家群体集S={s1,s2,…,s5}。由于存在语言信息且各属性都具有不同量纲与量级,因此需要进行一致化处理。现假设经二元语义[21-22](处理语言信息)和全序列法[18]动态无量纲处理后,属性的数据类型转化为实数型的“标准化数据”,如表3所示。
在此,将采用本文所提出的动态区间标度下的群组序关系评价法求得属性动态权重并进行方案的排序择优。由于上述问题的数据较多,因此在具体的计算过程中,部分数据省略,计算过程如下:
1) 数据的动态无量纲处理,处理过程简略,处理结果如表3所示。
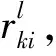
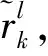

表3 供应商的原始评价信息一致化、无量纲处理后的数据

表4 不同时期专家给出的属性序关系及对应的理性赋值

续表(表4)

表5 各属性权重比值的理性赋值动态偏好区间
4) 由定理1及式(3)可求得每位专家判断下的属性区间权重:




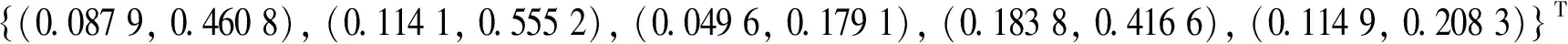
分两种情况考虑并集成求得属性的动态权重:
① 对于专家s1,s2给出的属性定性序关系一致情形。


最后通过式(6)对πk值进行归一化处理就得到属性序关系一致情形下的属性权重值:

W1=(0.330 4,0.237 7,0.093 9,0.199 7,0.138 3)T
② 对于专家s3,s4,s5给出的属性判断定性序关系不一致情形:

表7 各属性权重的排序向量

W2=(0.228 5, 0.231 9, 0.169 9, 0.166 1)T
再利用式(12)计算得到属性的动态权重值W=(w1,w2,w3,w4,w5)T。结果如下:
W=(0.269 3,0.234 2,0.139 5,0.202 0,0.155 0)T
5) 排序。按照式(13)计算出各被评价对象oi(i=1,2,3,4)的动态综合评价值yi。得:
y=(0.514 8,0.452 2,0.582 7,0.514 3)T
因此可得方案的排序结果为:s3≻s1≻s4≻s2。
从上述计算过程中可以看出,本文所提出的动态区间标度群组序关系评价法相比于区间标度群组序关系评价法考虑了时间价值与群体判断不完全一致情形,计算结果合理有效,很好地解决了属性权重不确定的动态综合评价问题,该方法更贴近实际且应用范围更广,也为后续的进一步研究提供了方向。
3 结束语
本文针对动态综合评价中属性权重不确定的问题进行了研究,并对区间标度群组序关系评价法进行了拓展,考虑了群体判断序关系不完全一致的动态评价情形,提出了一种新的求解属性动态主观权重的动态区间标度群组序关系评价法,并进行了方案的排序择优。综上所述,可知该方法具有以下几点特点:
1) 属性的权重分配差异度适中且合理。
2) 主观权重算法考虑了群体判断不完全一致情形,使得评价结果更贴近实际,更具合理性。
3) 将传统区间标度群组序关系分析法拓展到群体判断不完全一致的动态评价情形,使得传统方法的应用范围得到了延伸,方法的有效性与可行性也得到了进一步肯定。
4) 采用规划模型的方式来集结群体意见,更具客观性,能够很好地反应群体的偏好。
5) 所提出评价方法易于推广,可运用于评价信息为模糊数、直觉模糊数、不完全信息等多种信息形式共存的属性权重不确定的动态综合评价问题。
6) 运用全序列处理原始信息,避免了信息的失真与扭曲,同时考虑了属性值的横向动态增量信息,使得评价结果更具真实性。
7) 采用了定性与定量相结合的方法。
[1] 郭亚军.综合评价理论、方法及应用[M].北京:科学出版社,2007.
[2] 刘微微,石春生,李靖.基于双激励控制线的变化速度动态综合评价[J].中国管理科学,2010,18(专辑):23-28.
[3] 陈洪转,刘思峰,胡海东.基于双激励控制线的高校科研成果动态综合评价[J].科学与科学技术管理,2011,32(3):129-133.
[4] 王学军,郭亚军.三维动态、组合评价方法及其应用[J].工业工程与管理,2005(6):19-28.
[5] 王学军,郭亚军,赵礼强.一种动态组合评价方法及其在供应商选择中的应用[J].管理评论,2005,17(12):40-43.
[6] 边旭,田厚平,郭亚军.具有激励特征的供应商动态评价方法[J].南开管理评论,2004,7 (5):87-90.
[7] 郭亚军.一种新的动态综合评价方法[J].管理科学学报,2002,5(2):50-54.
[8] 易平涛,郭亚军,张丹宁.基于双激励控制线的多阶段信息集结方法[J].预测,2007,26(3):39-43.
[9] 马赞福,郭亚军,张发明,等.一种基于增益水平激励的动态综合评价方法[J].系统工程学报,2009,24(2):243-247.
[10] 张发明.基于双激励模型的动态综合评价方法及其应用[J].系统工程学报,2013,28(2):248-255.
[11] 杨茂,贾云彭,钱为,等.基于动态权重的风电功率组合预测方法研究[J].东北电力大学学报,2013,33(1/2):131-136.
[12] 李伟伟,郭亚军,易平涛.带有奖励作用的密度算子及应用[J].运筹与管理,2012,2(14):146-152.
[13] 何刚,魏连雨.建设项目多层次模糊评价及动态权重的确定[J].河北工业大学学报,2004,33(1).
[14] 镇长青.多目标决策中的权重调查方法[J].系统工程理论与实践,1987,7(4):23-26.
[15] XU Z S.Generalized chi square method for the estimation of weights[J].Journal of Optimation Theory and Applications,2000,107(1):183-192.
[16] 朱建军,刘土新,王梦光.一种新的求解属性区间数的判断矩阵权重方法[J].系统工程理论与实践,2005 (4):29-34.
[17] 张发明.区间标度群组序关系评价方法及其应用[J].系统工程学理论与实践,2013,33(3):720-725.
[18] 易平涛,张丹宁,郭亚军,等.动态综合评价中的无量纲化方法[J].东北大学学报,2009,30(6):899-902.
[19] 徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.
[20] 燕蜻.混合型多属性群决策方法研究[D].太原:山西大学,2012.
[21] 丁勇,梁昌勇,朱俊红,等.群决策中基于二元语义的主客观权重集成方法[J].中国管理科学,2010,18(5):165-170.
[22] 冒小芬,陈建明.基于比例二元语义的城市综合体风险评价[J].重庆理工大学学报(自然科学),2014,28(12):134-139.
