数字图像放大分数阶偏微分方程方法
2018-06-06郭琳琴
杨 艳,郭琳琴
(吕梁学院 数学系, 山西 吕梁 033000)
偏微分方程应用于图像处理过程是将问题转化为能量泛函的优化问题,它应用变分法得到二维抛物型偏微分方程,然后应用偏微分方程的数值方法求解图像问题。文献[1-2]给出图像放大模型的能量泛函式:
其中:u表示放大后的图像;u0表示在原图的基础上用简单插值方法得到的图像;Ω表示图像的紧支撑域。第1项称为正则项(或平滑项),起到消除图像灰度不连续的作用,第2项为保真项,起到保持边缘信息的作用。λ为正常数,称为正则化参数,它通过反复试验人为选定,用来平衡上述两项[1]。然而,在图像处理的实际应用中这种模型会出现“锯齿现象”[1]。
分数阶微分算子被广泛应用于实际研究中,其理论方法是将整数阶微分算子中的1阶导数、2阶导数改为分数阶导数,得到的结果比整数阶更贴近实际结果。采用同样的思路,将微分方程处理图像问题的能量泛函式中的整数阶微分算子改为分数阶微分算子。文献[3]中能量泛函式如下:
其中χΩ1是Ω1上的特征函数。文献[1]中能量泛函式改进为:
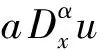
将图像放大问题转化为分数阶微分方程后,需考虑如何提高计算速度,得到更高收敛阶的算法。而一般高收敛阶的分数差分方法的边界条件需为零[4],显然一般的图像不具备这样的条件。
本文提出改进的分数阶图像放大模型,将能量泛函式中的导数改为α(1<α<2)阶Riesz分数阶导数,并用一种收敛阶为3-α的差分格式对其进行逼近求解,该方法对非零的边界条件也有效。实验结果表明:该方法能较好地保留图像的边缘特征和细节信息,同时运算时间较短,是一种有效、可行的图像放大算法。
1 相关理论
1.1 分数阶导数
关于分数阶导数目前有3种经典定义:Riemann-Liouville(R-L)、Capotu(C)和Grumwald-Letnikov(G-L),其中 R-L分数阶导数定义为:在有限区间[a,b],
(1)
(2)

(3)
为α阶Riesz分数阶导数[2]。
1.2 分数阶导数的差分格式
当1<α≤2时,Riemann-Liouvill分数阶导数能写成Hadamard有限积分部分,
(4)

(5)

(6)
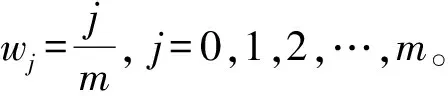
定理1 当1<α≤2时,假设u∈C3[a,b],令xm=a+mh,其中h=(b-a)/M,则
(7)
当m=2或m-M=-2时,
当m≥3且-M+m≤-3时,
(8)
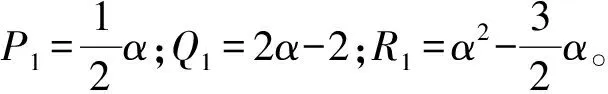
(9)
Qi=φi(i-2,i)-φi-1(i-2,i)
(10)

(11)
φi(a,b)=α(α-1)i2-α+α(2-α)(a+b)i1-α+(2-α)(1-α)abi-α
(12)

此时g(w)=g2(w)+O(h3)。
另一方面,式(6)中,第1个区间包含w=w0=0的奇异点,需用Hadamard有限积分式(5)计算,其他区间为正常积分[4]。当j=2,3,…,m时,

由式(9)~(12)符号的引入,得
(13)
类似地,当j=1时,由式(5)得
(14)
将式(13)~(14)代入式(6)整理得
(15)
其中:
(16)
同理可得,
带状疱疹后遗神经痛(Postherpetic Neuralgia,PHN)是带状疱疹(Herpes Zoster)最常见的并发症,指带状疱疹皮损愈合后疼痛持续超过1月者,好发于体质虚弱者和老年人[1] 。该病以剧烈的烧灼样、电击样、撕裂样疼痛为临床特征,缠绵难愈,严重损害患者的情感、睡眠和生命质量[2] 。其治疗方法较多,但治愈率低。笔者采用针刺配合热敏灸治疗PHN42例,取得较好疗效,现报道如下。
(17)
综合式(15)~(17),结论成立。
由定理1得分数阶Riesz导数的近似算法为
(18)
2 基于分数阶的图像放大算法
2.1 模型的建立
文献[1]中引入如下能量泛函式:
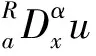
利用变分法推得的该泛函欧拉-拉格朗日方程如下:
其中:
则有如下结果:
(19)
(20)

(21)
利用梯度下降法得到相应的扩散方程为
(22)

(23)
右端项中分数阶导数使用式(7)~(12)和(18)离散,其中空间步长h=1。
2.2 模型的算法

第2步利用式(22)对u0进行修正。考虑到灰度值属于整数集,而式(18)中wj<10-2(|j|>2),将式(22)的分数阶导数只用自身与其左右各两项共5项的线性组合逼近,即将式(18)改为
3 实验结果
实验中选取240像素×240像素大小的灰度图进行仿真实验。为了测试算法的有效性,首先将原始图像缩小1/2作为缩小采样,然后采用三次样条插值方法将其放大,最后采用本文算法对该放大结果进行修正。实验中的离散化参数选取如下:λ=0.5,h=1,Δt=0.05,α=1.7,迭代20次。

图1 图像放大实验结果

选择算法峰值信噪比PSNR本文算法结果40.370 9文献[1]算法结果39.125 0
从图1的图像放大实验结果可见,本文和文献[1]的算法均保留了原图像的特征,在视觉上有较好的效果,但区别不明显。从表1的图像放大结果的峰值信噪比可见,本文算法结果更接近于原图,优于文献[1]的算法结果。
为了进一步对本文算法和文献[1]算法进行比较,分别选取原始图像、文献[1]放大结果图像和本文放大结果图像的第50行,对其灰度值曲线进行比较,所得结果如图2所示。
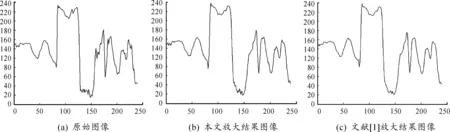
图2 图像放大前后第50行灰度曲线比较
通过对图2(a)和(b)进行比较可以看出:本文算法有较好的整体效果,虽然放大结果相比原图略有平滑,但较文献[1]的算法在细节、边缘方面的清晰度都有明显改善,更好地保留了原始图像的边缘锐度和纹理特征。
4 结束语
本文提出了一种改进的基于分数阶偏微分方程的图像放大模型,在模型中使用收敛阶为3-α的差分格式对α阶Riesz分数阶导数进行逼近求解。实验仿真结果表明:该算法能较好地保留图像的边缘信息和纹理特征,得到较为清晰、更接近原始图像的放大结果,是一种可行的数字图像放大算法模型。在实验中用到的参数为多次实验的经验值,如何确定较好的参数以保证较好的放大效果有待进一步研究。
[1] 高冉,顾聪,李胜宏.基于分数阶偏微分方程的图像放大模型[J].浙江大学学报(理学版),2016,5(43):550-553.
[2] 宋锦萍,高冉,朱芳,等.PDE技术的图像放大模型[J].中国图象图形学报,2009,14(1):82-87.
[3] GAO Ran,SONG Jinping,TAI Xuecheng.Image zooming algorithm based on partial differential equations technique[J].International Journal of Numerical Analysis and Modeling,2009,6:5-18.
[4] 刘发旺,庄平辉,刘青霞.分数阶偏微分方程数值方法及其应用[M].北京:科学出版社,2015.
[5] DIETHELM K.Generalized compound quadrature formula for finite-part integral[J].IMA J Number Anal,1997,17:479-493.
[6] YAN Y,PAL K,FORD N J.Higher order numerical methods for solving fractional differential equations[J].BIT Number Math,2014,54:555-584.
[7] 朱宁,吴静,王忠谦.图像放大的偏微分方程方法[J].计算机辅助设计与图形学报,2005,17(19):1941-1945.
[8] 阮秋琦,忤冀颖.数字图像处理中的偏微分方程方法[J].信号处理,2012,28(3):301-314.
