Ti-Al金属间化合物的力热性能及其能带计算*

郭连权， 刘冰冰， 马 贺， 李大业

(沈阳工业大学 a. 理学院， b. 基础教育学院， 沈阳 110870)

几十年来，针对航空应用钛合金的研究取得了很大的进展，许多钛合金在航空领域得到了广泛应用.钛合金不仅具有强度高、密度小、耐高温和抗腐蚀性好等优点，还可以减轻发动机质量，有利于提高发动机推重比并提高发动机性能，因而在高温工作环境下可以替代耐热不锈钢、镍基高温合金等.很多学者针对Ti-Al二元系合金进行了多方面研究[1]，例如利用F-S模型分别计算了TiAl相的晶格常数、结合能、弹性常数和点缺陷形成能；利用第一性原理对TiAl相的基本物理性能以及Ti-Al合金的结构稳定性、电子和弹性性质进行了研究；采用Materials Studio软件与第一性原理对Ti-Al合金的力热性能、电子结构以及Ti-Al合金中多个合金相的力学性能进行了相关研究；采用EAM模型分析了TiAl金属间化合物的相关力学性能；基于密度泛函理论对TiAl3相的结构、电子性质、动力学性质和生成热进行了研究等.具体而言，李明曼利用第一性原理对钛合金的稳定性及弹性模量进行了系统计算[2]；Wang等对Mo掺杂TiAl合金的性能进行了第一性原理计算[3]；Stocks等利用第一性原理对TiAl合金的晶格常数进行了优化，并进行了一系列理论计算[4]；Adebambo等采用广义梯度近似(GGA)方法对钛合金的电子结构进行了分析[5]；Shu等利用第一性原理对经过第三元素掺杂的Ti-Al合金的晶格常数、电子结构与弹性系数进行了研究[6]；Hussain等利用第一性原理对TiAl3相的电子结构进行了理论分析[7]；Ye等针对氢含量对TiAl-Ti3Al系统力学性能的影响进行了第一性原理研究[8].上述研究成果为Ti-Al合金的应用提供了理论参考和依据.本文采用密度泛函理论及第一性原理并利用Materials Studio软件中的CASTEP软件包，对Ti-Al合金中的4种主要金属间化合物的相关力热性能和电子能带进行了理论计算，以期为Ti-Al合金的理论研究和实际应用提供有益参考.

1 计算模型与方法

1.1 计算模型

Al晶体为面心立方(fcc)结构，属于Fm3m空间群，其晶格常数a=b=c=0.404 84 nm且α=β=γ=90°.Ti晶体为六方密堆积(hcp)结构，属于P63/mmc空间群，其晶格常数a=b=0.294 59 nm、c=0.463 87 nm；α=β=90°、γ=120°.Al和Ti的晶体结构如图1所示.

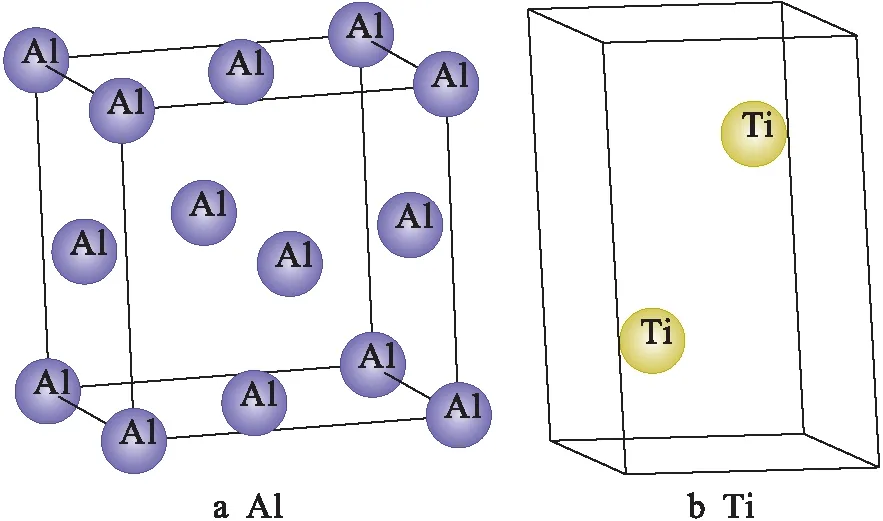
图1 Al和Ti的晶体结构Fig.1 Crystal structures of Al and Ti

本文基于Materials Studio软件中的Visualizer程序包构建了Ti-Al合金中4种金属间化合物模型，分别为TiAl(P4/mmm)模型、TiAl2(Cmmm)模型、TiAl3(I4/mmm)模型和Ti3Al(P6/mmm)模型.Ti-Al合金中4种金属间化合物具体模型如图2所示，其中深色球代表Al，浅色球代表Ti.

图2 Ti-Al合金结构模型Fig.2 Models for structures of Ti-Al alloy

1.2 计算方法

本文计算是利用Materials Studio软件中的CASTEP软件包并基于密度泛函理论的第一性原理进行的.首先对Al、Ti的晶格常数进行了计算，并对其结构进行优化，且单个原子精度为5×10-7eV.当对Ti晶体结构进行优化时，截断能为350 eV，K点网络数目为3×3×3；当对Al晶体结构进行优化时，截断能也为350 eV，K点网络数目为6×6×6.当对晶格常数进行计算时，分别采用了广义梯度近似方法的PBE与PW91计算方法以及局域密度近似(LDA)方法.Al和Ti晶格常数的计算结果如表1所示.由表1可见，与晶格常数经验值相比，采用广义梯度近似方法中的PBE计算方法效果最佳，这与之前某些学者的研究结果一致[9-11].

2 计算结果与分析

2.1平衡晶格常数

针对Ti-Al合金中的TiAl、TiAl2、TiAl3和Ti3Al 金属间化合物进行了几何结构优化.当计算晶体能量时，采用广义梯度近似方法中的PBE计算方法进行优化，而当计算弹性常数时，则利用广义梯度近似方法中的PW91计算方法进行优化.当对TiAl、TiAl2、TiAl3和Ti3Al进行优化时，K点网络数目依次取为9×9×6、7×7×6、7×7×9和3×3×6.在优化过程中均采用固体物理学原胞进行计算.优化后4种金属间化合物的晶格常数与经验值如表2所示.

表1 Al和Ti晶格常数的计算结果Tab.1 Calculated results for latticeconstants of Al and Ti nm

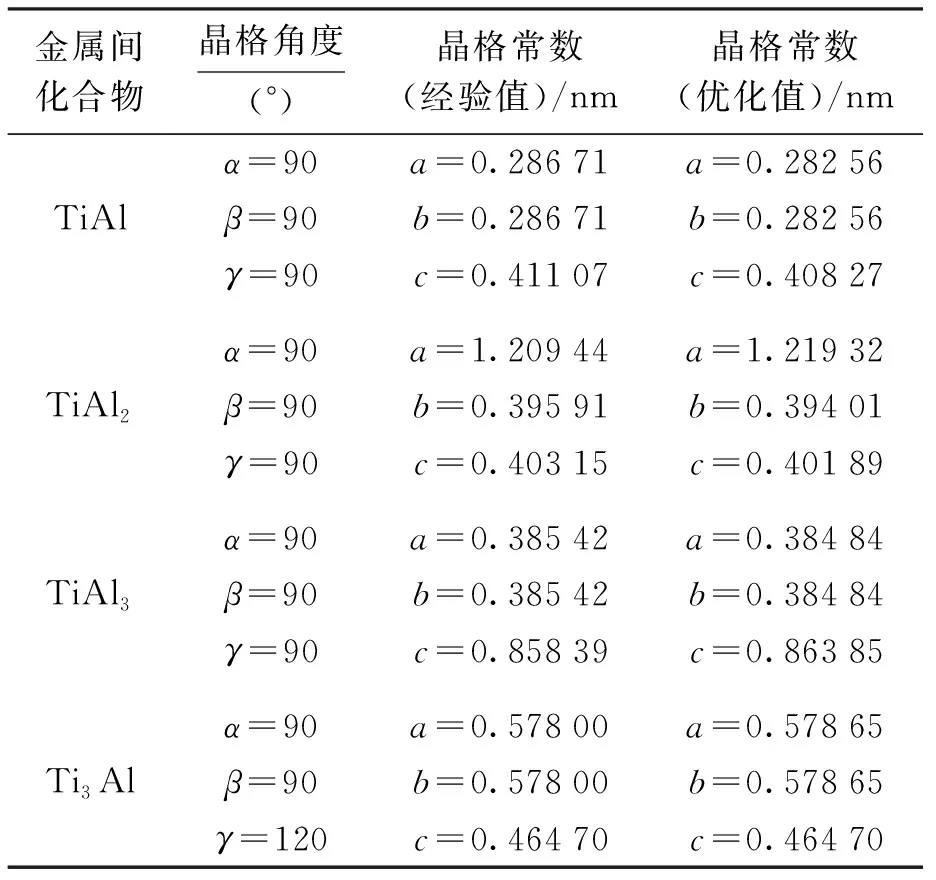
表2 Ti-Al合金中金属间化合物的晶格常数Tab.2 Lattice constants of intermetalliccompounds in Ti-Al alloy

2.2 生成热与结合能

晶体的生成热是指常态下纯元素形成化合物时释放的能量.生成热越低，则该晶体的生成能力越强[12].生成热计算公式为

(1)

式中：Etoi为Ti-Al系合金中金属间化合物在平衡晶格常数下平均单个原子的总能量；N和Esolid分别为某种元素的原子个数以及固态下某种元素单个原子的基态能量；A、B分别为两种原子代号.

晶体的结合能是将晶体分解成单个原子需要的能量.结合能绝对值越大，则形成的中间相稳定性就越高[13].结合能计算公式为

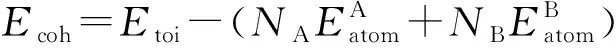
(2)

式中，Eatom为自由状态下某种元素单个原子的能量.

在几何结构优化的基础上，利用CASTEP软件包计算得到了不同金属间化合物的基态能量，并利用上述公式计算出了各个金属间化合物中单个原子的生成热和结合能，具体结果如表3所示.

表3Ti-Al合金中金属间化合物单个原子的生成热与结合能

Tab.3FormationenthalpyandcohesiveenergyforsingleatomofalloyintermetalliccompoundsinTi-Alalloy

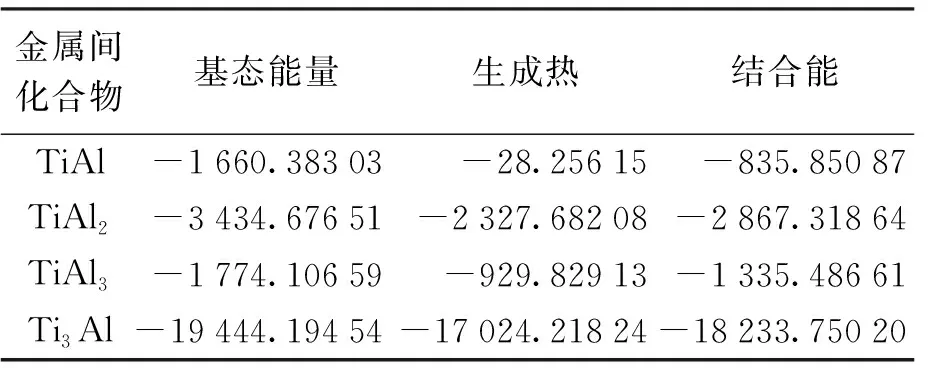
eV

由表3可见，金属间化合物TiAl、TiAl2、TiAl3和Ti3Al的生成热均为负值，表明4种金属间化合物均能形成.通过对4种金属间化合物的生成热数值进行比较可知，Ti3Al相的生成热数值最低，由生成热定义可知，生成热越低，其合金化能力越强，因此，Ti3Al相是在Ti-Al合金形成过程中最容易形成的相.相对Ti3Al相而言，TiAl与TiAl3相都是不容易生成的相.观察表3可知，Ti3Al相的结合能绝对值最大，因而其晶格稳定性最高，而TiAl相的结合能绝对值最小，因而其晶格稳定性最低.结合生成热和结合能的计算结果可知，Ti3Al相不仅容易形成，且其晶格稳定性也是最高的.

2.3 弹性性质

在几何结构优化的基础上，分别对Ti-Al合金中的4种金属间化合物的弹性常数进行了计算，同时计算了4种金属间化合物的体模量B、压缩系数C、杨氏弹性模量E、剪切模量G和泊松比v，具体计算结果如表4所示.

体模量表征材料在外加应力作用下抵抗变形的能力.由表4可知，Ti3Al相的体模量最大，因而其抗变形能力最强，而TiAl2相的体模量数值最小，故其抗变形能力相对最小.压缩系数是描述物体压缩性大小的物理量.观察表4可以发现，TiAl2相的压缩系数最大，进而得出其压缩性能最好，而Ti3Al相的压缩系数相对较小，因而其压缩性能相对差一些.剪切模量体现了材料的抗剪切能力，剪切模量越大，则材料的抗剪切能力越强.表4中TiAl3相的剪切模量最大，因而TiAl3相的抗剪切能力最强.剪切模量与体模量的比值G/B可以作为金属韧脆性的经验判据[14].当G/B<0.57时，材料表现为韧性，且G/B值越小，材料的韧性与延展性越好；当G/B>0.57时，材料则表现为脆性，且G/B值越大，脆性越显著.由表4可见，TiAl和Ti3Al相均表现为韧性，而TiAl3和TiAl2相均表现为脆性.杨氏弹性模量表征了材料 的刚度，且杨氏弹性模量越大，材料的刚度越大.由表4可以观察到，Ti3Al相的杨氏弹性模量最大，表明其刚度最大，与之相比TiAl相的刚度最差.泊松比表征了材料塑性的强弱.观察表4可知，Ti3Al与TiAl3相的泊松比相对较小，因而其塑性相对较差.

表4 Ti-Al合金中金属间化合物的弹性系数Tab.4 Elastic coefficients of intermetallic compounds in Ti-Al alloy

2.4 能带与态密度

能带曲线能够显示出空带、价带与导带的范围，而能隙处于价带顶和导带底之间.当能隙很小或为零时，该材料为金属性材料，在室温下电子很容易获得能量并跳跃至导带而发生导电.当能隙很大(大于9 eV)，该材料为绝缘体，电子很难跳跃至导带，因而无法导电.一般情况下当能隙处于1～3 eV时，该材料为半导体材料[15].

本文在计算能带和态密度时，仅考虑费米面处较近的电子结构情况.图3～6为4种金属间化合物TiAl、TiAl2、TiAl3和Ti3Al的能带曲线.

图3 TiAl能带Fig.3 Energy band of TiAl

由图3～6可以直观地观察到不同金属间化合物的能带幅度变化和能级穿越情况，且4种金 属间化合物均属于金属性材料.由能级穿越费米面的情况可知，4种金属间化合物中Ti3Al相的金属性最强，TiA13相的金属性最弱.

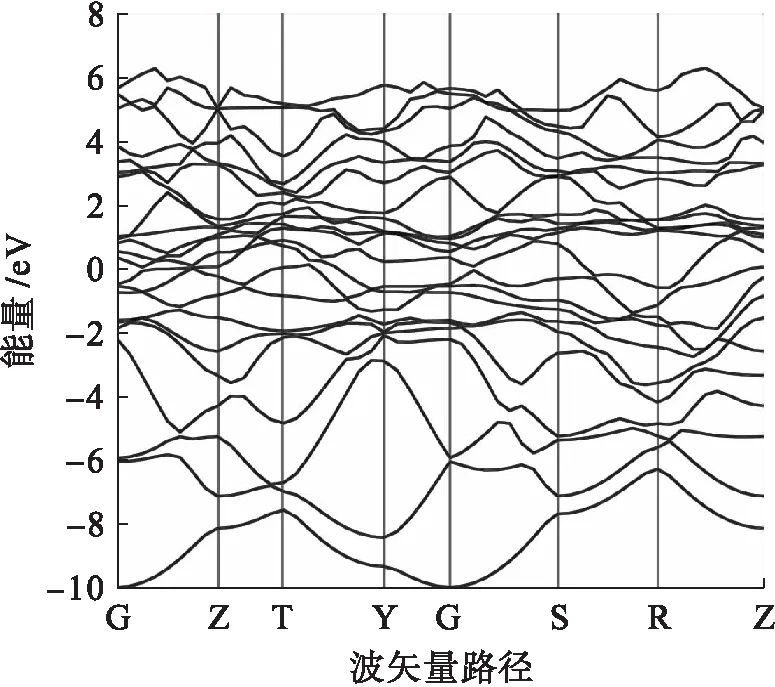
图4 TiAl2能带Fig.4 Energy band of TiAl2

图5 TiAl3能带Fig.5 Energy band of TiAl3

图6 Ti3Al能带Fig.6 Energy band of Ti3Al

单位能级范围内允许出现电子的量子态数目称为电子态密度，它是描述电子结构的一种方式.图7为金属间化合物TiAl的总态密度和分波态密度曲线.由图7可知，在费米能级左侧-2 eV附近出现的态密度峰是由Al的3p态和Ti的3d态共同贡献的.费米能级左侧-0.3 eV附近出现的峰值，以及费米能级右侧2 eV与4 eV附近出现的峰值主要是由Ti的3d态贡献的.

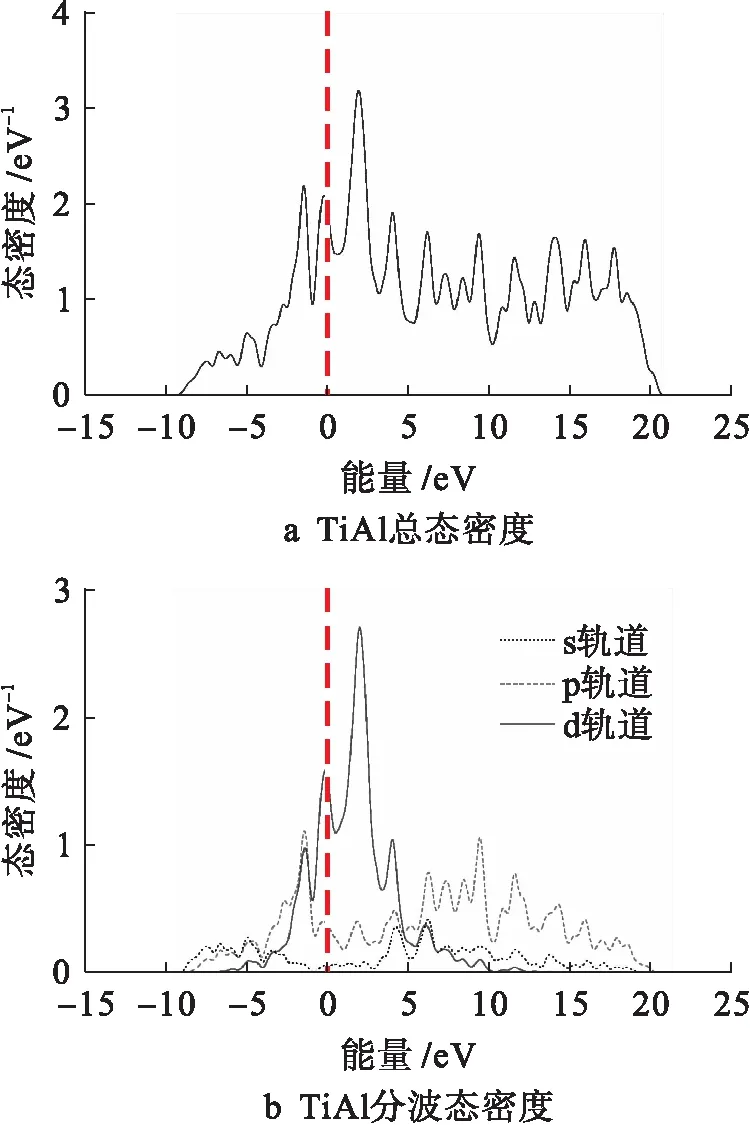
图7 TiAl总态密度和分波态密度Fig.7 Total and partial density of states for TiAl

图8为金属间化合物TiAl2的总态密度和分波态密度曲线.由图8可知，费米能级左侧-2 eV至费米能级处的TiAl2连体峰主要是由Al的3p态和Ti的3d态共同贡献的，而费米能级右侧2 eV处附近出现的最大峰值主要是由Ti的3d态贡献的.

图9为金属间化合物TiAl3的总态密度和分波态密度曲线.由图9可知，费米能级左侧-1.5 eV附近的Ti3Al峰值主要是由Al的3p态和Ti的3d态共同贡献的，而费米能级右侧2.3 eV附近的峰值主要是由Ti的3d态贡献的.

图10为金属间化合物Ti3Al的总态密度和分波态密度曲线.由图10可知，从费米能级左侧-2.3 eV至费米能级右侧1eV的能量区间内的态密度连体峰主要是由Ti的3d态贡献的.

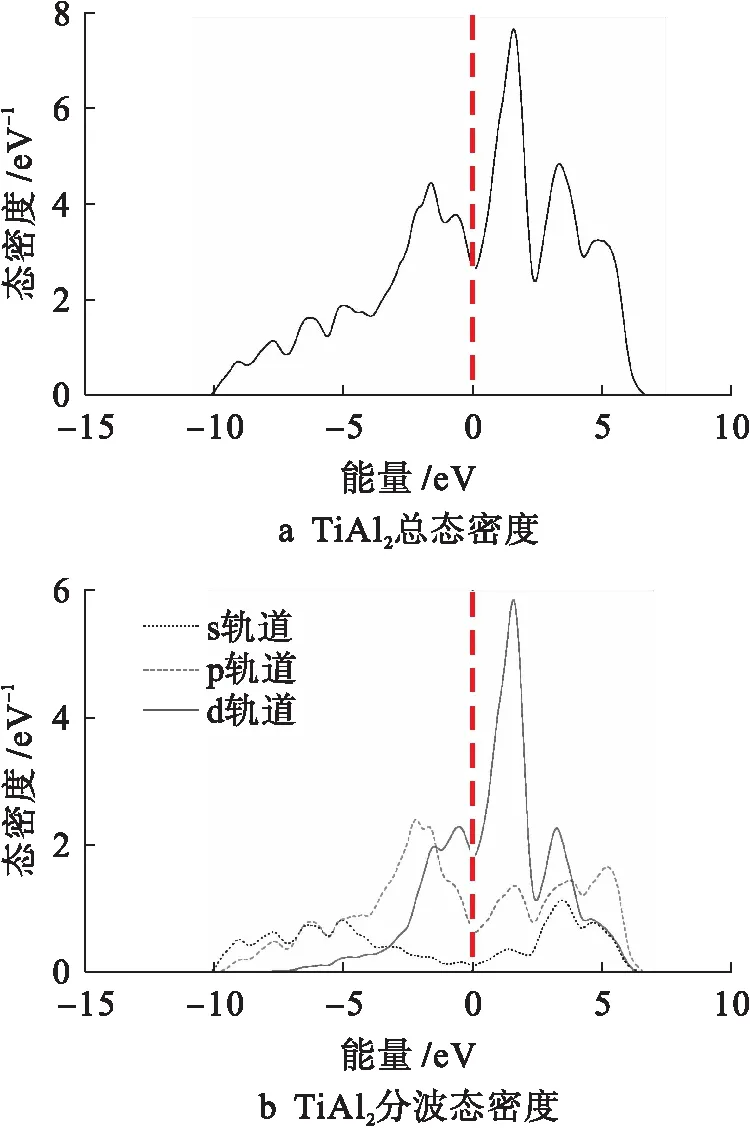
图8 TiAl2总态密度和分波态密度Fig.8 Total and partial density of states for TiAl2

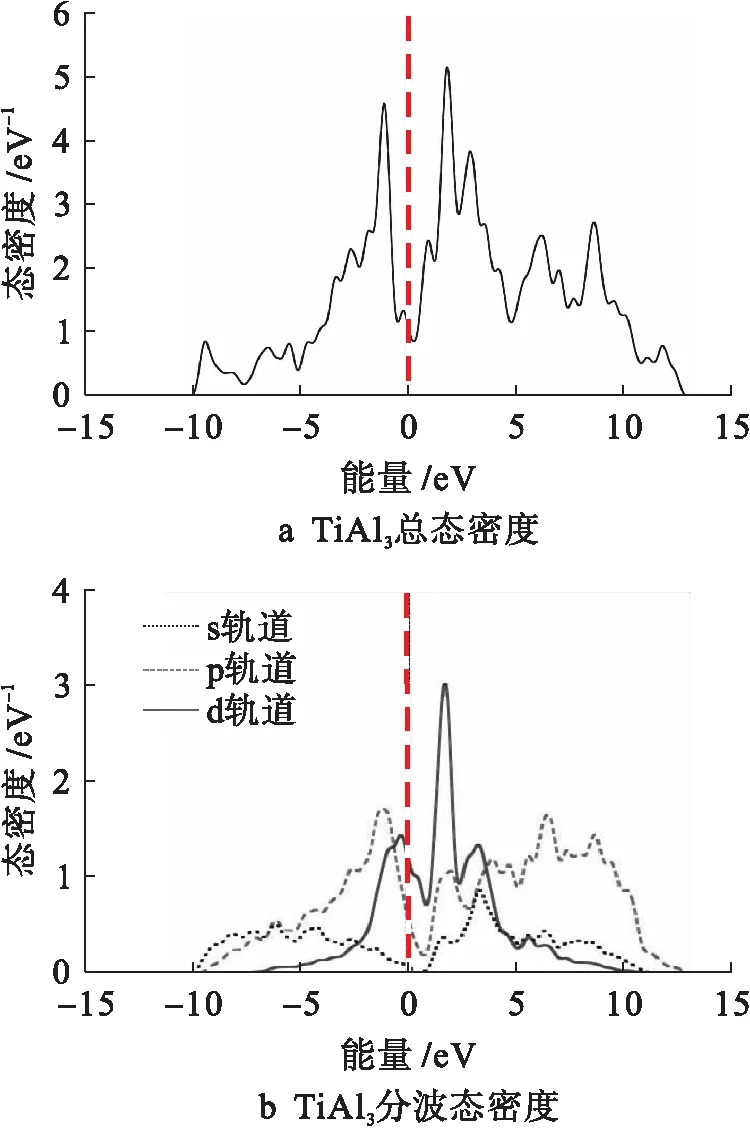
图9 TiAl3总态密度和分波态密度Fig.9 Total and partial density of states for TiAl3

3 结 论

通过对Ti-Al合金中金属间化合物TiAl、TiAl2、TiAl3和Ti3Al的生成热、结合能、弹性系数和电子结构进行计算与分析，可以得到如下结论：

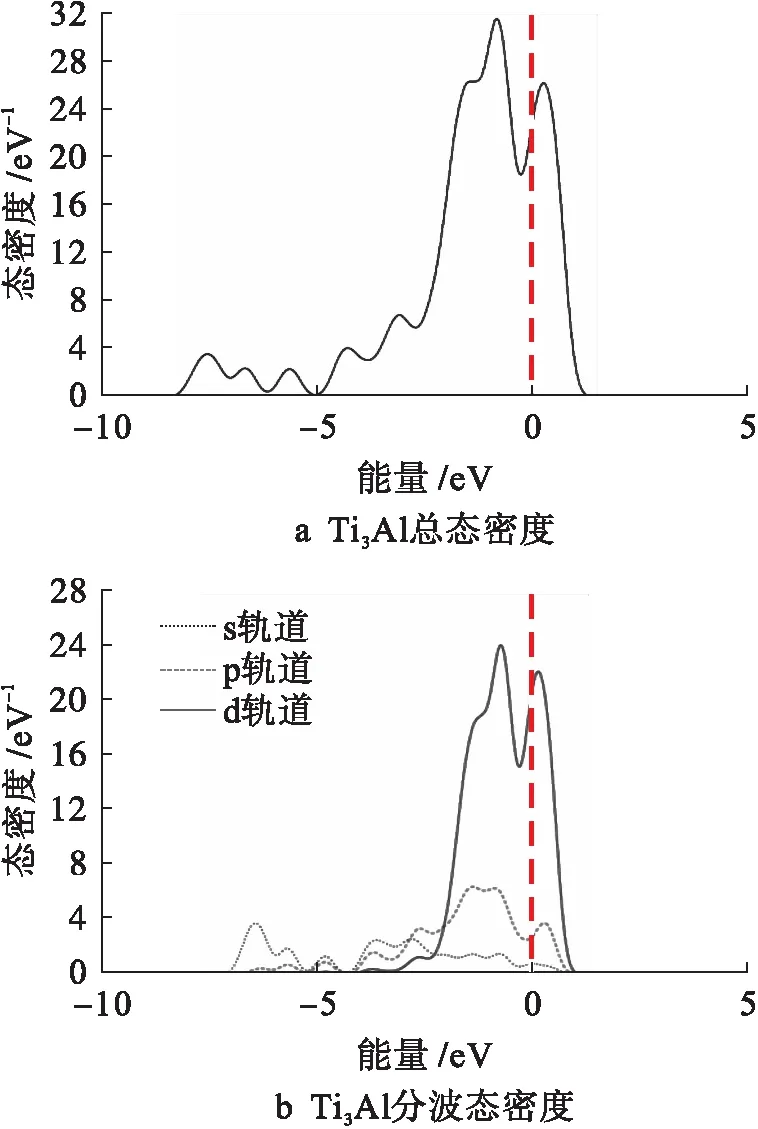
图10 Ti3Al总态密度和分波态密度Fig.10 Total and partial density of states for Ti3Al

1) 4种金属间化合物中Ti3Al为合金化形成能力最强且最稳定的中间相；

2) 4种金属间化合物中Ti3Al呈韧性，抗变形能力最强且刚度最大；

3) TiAl、TiAl2Ti3Al和TiA13均属于金属性材料，且Ti3Al相金属性最强，而TiA13相金属性最弱.

参考文献(References)：

[1] Wang H Y，Li C Y，Gao J，et al.First-principles studies of the structural and thermodynamic properties of TiAl3under high pressure [J].Acta Physica Sinica，2013，62(6)：675-676.

[2] 李明曼.第一性原理方法β-钛合金中非平衡相稳定性及弹性模量的研究 [D].烟台：烟台大学，2014.

(LI Ming-man.Study in equilibrium phase stability and elastic modulus ofβ-titanium alloy by first principles method [D].Yantai：Yantai University，2014.)

[3] Wang H Y，Li C，Li X，et al.Influence of Mo doping on the physical properties of TiAl alloy by the first principles [J].Rare Metal Materials & Engineering，2015，44(11)：2737-2741.

[4] Stocks G M，Pope E P，Giamei A F，et al.Alloy phase stability and design [J].Materials Research Society Symposia，2014，186：277-282.

[5] Adebambo P O，Adetunji B I，Olowofela J A，et al.Structural，electronic，magnetic and optical properties of Ni，Ti/Al-based heusler alloys：a first-principles approach [J].Zeitschrift Für Naturforschung A，2016，71(2)：129-134.

[6] Shu S L，Tong C Z，Qiu F，et al.Effects of ternary elements on the ductility of TiAl [J].Canadian Metal-lurgical Quarterly，2016，55(2)：156-160.

[7] Hussain A，Mehmood S，Rasool N，et al.Electronic structure，mechanical and optical properties of TiAl3(L12& D022) via first-principles calculations [J].Chinese Journal of Physics，2016，54(3)：319-328.

[8] Ye W，Ying Z.A first-principles study of site occupancy and interfacial energetics of an H-doped TiAl-Ti3Al alloy [J].Science China Physics，Mechanics & Astronomy，2012，55(2)：228-234.

[9] Mattsson A E，Armiento R，Schultz P A，et al.Nonequivalence of the generalized gradient approximations PBE and PW91 [J].Physical Review B，2012，73(19)：1-7.

[10]李思.新型纳米光电子材料的第一性原理研究 [D].北京：华北电力大学，2011.

(LI Si.The first-principles study on new nano-photo-electron materials [D].Beijing：North China Electric Power University，2011.)

[11]王和雪松.高温高压下YBa2Cu3O7物理性质的第一性原理计算 [D].成都：四川师范大学，2013.

(WANG He-xuesong.First-principles study for YBa2Cu3O7physical properties under high temperature and pressure [D].Chengdu：Sichuan Normal University，2013.)

[12]马贺.Al-Cu-Mg-Y系合金的性能与第一原理计算 [D].沈阳：沈阳工业大学，2015.

(MA He.Performances and first-principle calculation of Al-Cu-Mg-Y alloys [D].Shenyang：Shenyang University of Technology，2015.)

[13]林琳.铝镁硅合金的结构表征及其力热性能的计算 [D].沈阳：沈阳工业大学，2015.

(LIN Lin.Al-Mg-Si alloy structure characterization and its thermodynamic properties calculation [D].Shenyang：Shenyang University of Technology，2015.)

[14]郭连权，林琳，马贺，等.Mg2Si的声子谱与力热性能的第一性原理计算 [J].沈阳工业大学学报，2015，37(3)：294-298.

(GUO Lian-quan，LIN Lin，MA He，et al.First-principle calculation on phonon spectrum and thermodynamic properties of Mg2Si [J].Journal of Shenyang University of Technology，2015，37(3)：294-298.)

[15]杨金.非挥发性阻变存储器阻变机理及性能研究 [D].合肥：安徽大学，2014.

(YANG Jin.Research on resistive switching mecha-nism and performance for non-volatilie resistive switching memory [D].Hefei：Anhui University，2014.)