基于不同角部方案的RC结构抗连续倒塌设计*

刘成才

(中州大学 土木工程学院， 郑州 450044)

建筑结构的连续倒塌是指由于某些因素引起的结构系统内部的局部初始破坏，这种初始破坏在系统内发展、传播，进而导致结构整体的破坏倒塌[1].连续倒塌的原因可以归结为两类[2]：第一类是由于地震作用，结构进入非弹性大变形，构件失稳，传力路径失效引起连续倒塌；第二类是由于撞击、爆炸、火灾及施工设计的失误或人为破坏等造成部分承重构件的失效，阻断传力路径导致连续倒塌.结构若发生连续倒塌，特别是类似“9·11”等事件的发生，将造成较大的人员伤亡、财产损失，因此，结构抗连续倒塌问题的研究与设计逐渐成为工程界关注的对象.

欧洲与北美国家经过多年研究，已将抗连续倒塌设计思想编入规范，如美国GSA 2003(该设计准则给出了一套抗连续倒塌设计的结构分析流程)、DoD 2010英国建筑规程(British Standard)[3]、欧洲规范(Eurocode 1)及加拿大建筑规程(NBCC)[4]等.在国内，对于结构局部的小范围破坏(例如钢筋混凝土构件裂缝问题)而导致结构破坏的分析可见文献[5].

在进行结构抗连续倒塌研究中，一般可假设这些初始破坏发生在结构的关键部位，以最不利情况进行分析.DoD 2010建议以结构的角部、边缘及内部竖向承重构件作为典型构件，通过移除这些构件模拟初始局部破坏.建筑结构设计实践中，结构关键部位的杆件布置可能有多种方案.目前，针对不同结构布置方案，研究在偶然荷载作用下抗连续倒塌性能的文献尚不多见.本文基于不同角部结构方案，设计了3栋6层钢筋混凝土框架结构建筑，分别布置3种不同角部拉结方案并进行了分析，比较研究结构在不同角部结构方案下的抗连续倒塌性能.

1 有限元模型

1.1 框架结构模型设计

本文设计分析模型利用PKPM(V3.1.5)软件，并依据我国现行国家规范[6-7]进行配筋设计.框架结构共6层，层高3.3 m，柱网尺寸7.2 m×7.2 m，建筑场地设定为Ⅱ类场地，设计地震分组为第1组，抗震设防烈度为6，地面粗糙度为B类；楼面恒载为5.0 kN/m2，楼面活载为2.5 kN/m2，屋面恒载为5.5 kN/m2，屋面活载为2.0 kN/m2；外墙另设6.6 kN/m线荷载，柱截面尺寸为500 mm×500 mm，梁截面尺寸为250 mm×600 mm，楼面板厚100 mm，屋面板厚120 mm；混凝土强度等级C30，受力钢筋及箍筋均采用HRB400级.

典型框架结构的角部布置方式如图1所示，在结构扭转变形不大的情况下，可采用模型1，即不作任何拉结的处理方式；在角柱有较大扭转变形情况下，可采用模型2的处理方式，将角柱与相邻内柱拉结；当结构角部有较大范围的扭转变形时，可采用模型3的处理方式，即将相邻边柱进行拉结.本文建立框架结构方案设定单一变量，即平面角柱与周边采用3种不同拉结方式：模型1，角柱与相邻边柱拉结；模型2，角柱与相邻内柱拉结；模型3，角部相邻边柱拉结.

1.2 分析方法

建筑结构抗连续倒塌性能分析一般采用以下两 种方法：一是拆除构件分析方法[8]，二是Pushdown分析方法[9].本文运用第一种方法进行分析，分析过程为：通过静力分析得到失效构件(柱)的内力，然后取消构件，再将构件的内力反向加载到节点，从而实现模拟失效构件的目的.

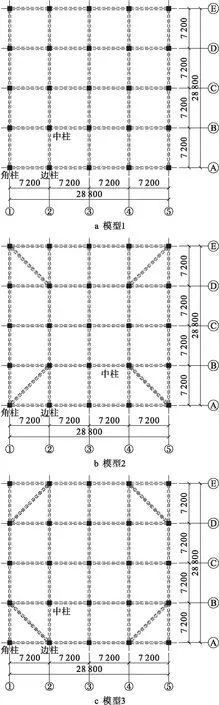
图1 结构模型平面布置图(单位：mm)Fig.1 Plane arrangement diagram ofstructural model (unit：mm)

参照GSA 2003中的荷载组合作为常规荷载进行动力分析，即

LLoad=1.0D+0.25L

(1)

式中：D为恒定载荷；L为活动载荷.选择强度和变形的双重准则，即以不出现失效铰及塑性铰转角θ≤6°作为判断连续倒塌的依据[10].

1.3 拉结梁基本原则及假定

根据清华大学陆新征[11]等对钢筋混凝土框架结构抗连续倒塌设计的研究方法，提出了拉结设计中的基本原则：

1) 结构柱拆除后，与之相连接的梁同时存在梁机制(即梁端塑性铰的抗弯强度)和悬链线机制(即贯穿梁纵筋的抗拉强度)；

2) 对于梁机制，仅考虑梁端塑性铰对负弯矩的抗弯能力；

3) 拉结构件应具有足够的变形能力和抗剪强度.

对于上述第3点，文献[11]考察失效柱内力时，仅考虑其轴力，但在本文设定的不同角部方案中，还需要考虑拉结梁的弯矩及剪力.

1.4 SAP2000连续倒塌动力分析

应用SAP2000对3个结构模型进行非线性分析，具体过程如下：

1) 建立模型，进行静力计算及模态分析，得出结构在荷载组合下失效构件的内力及第1、3振型周期(因结构平面为对称布置，1、2振型周期相同，故取1、3周期).对于柱结构，由于计算所得剪力与弯矩相对轴力均较小，因此，分析只考虑轴力影响.结构自振周期及柱轴力情况如表1、2所示.

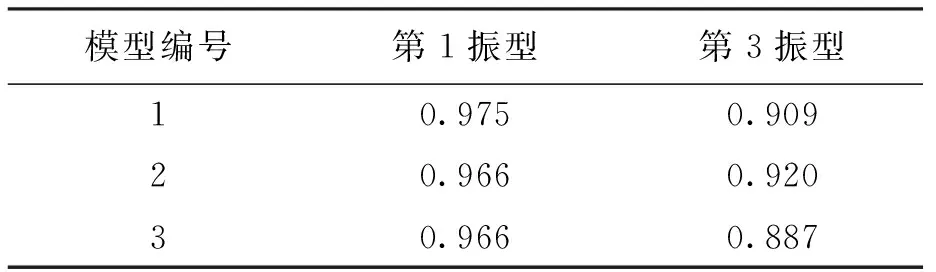
表1 结构自振周期Tab.1 Natural vibration period of structures s

表2 失效/拆除柱轴力Tab.2 Axial force of failed/removed columns kN

通过参考规范GSA 2003及DoD 2010中有关拆除框架结构中不同部位柱相对重要程度的规定得出框架结构体系内不同部位柱构件的重要性排序，由高到低依次为底层外围柱、底层内部柱、上部外围柱和上部内部柱[12].

本文考察角部不同结构方案的布置，因底层柱较其他结构层更为重要，因此在房屋建筑的结构设计时，结构设计人员一般会采取诸如增大该层混凝土强度等级、增加柱截面配筋率等措施以提高柱结构安全储备.在常规荷载作用之余，若突发偶然荷载或作用(例如爆炸、地震、撞击等)时，结构竖向构件应具有较高的安全储备予以抵抗.然而在这种情况下，第2层及以上结构层的柱构件在偶然荷载下反而显得更为薄弱(例如，恐怖袭击飞机撞击时，其目标因周围有建筑的遮挡，飞机一般倾向于建筑的中部，而不易撞向结构底部)，因此，基于上述边界条件，本文选择了底层外最不利的情况，即在第2层某根角柱失效情况下进行结构抗倒塌性能分析.结构模型1的初始状态及结构2层柱失效的终态模型(显示拆除杆件的一瞬间，由于竖向荷载的持续作用产生的变形)如图2所示(图2a中，蓝色为柱、梁，红色为板).

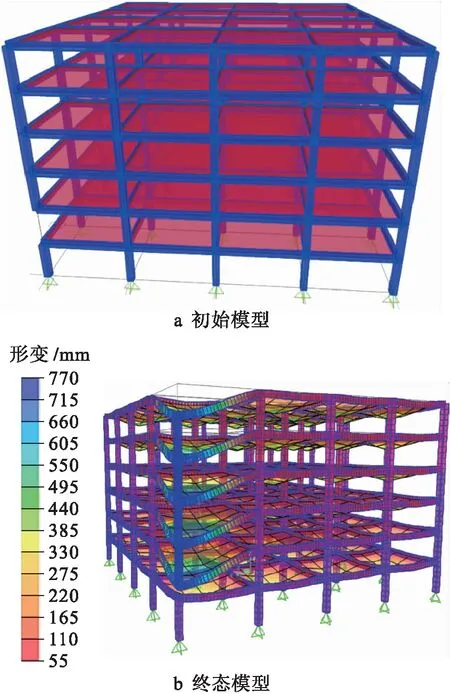
图2 结构模型1初始状态与终态Fig.2 Initial and final states of structural model 1

2) 拆掉失效柱，然后在失效柱点上反向设置点荷载(即失效柱的内力)进行拟定荷载组合下的非线性静力分析.

3) 在非线性分析基础上加载荷载，由于未破坏结构与拆除后结构的自振周期接近，因此，拆除后结构的自振周期可由未破坏结构的自振周期来近似取值.本文取未破坏结构自振周期的1/10作为失效时刻.将分析采用的时程工况定义为不考虑压变效应和楼板抗倒塌作用的情况，时程类型采用直接积分法，利用RAMPTH函数进行荷载施加.

4) 对3个模型进行时程动力计算.在时程荷载工况定义过程中，定义时程工况为初始条件.参照SAP2000的程序规范，在进行动力时程分析时，一般情况下使用非线性直接积分类型工况来完成连续的时程分析，即完整非线性分析.因为对线性时程工况指定初始荷载时，会考虑前工况非线性刚度影响，但不会考虑后续附加的非线性影响.

2 计算结果分析

2.1 失效柱点位移分析

设3个模型的第2层某角柱失效，分析得到3个模型结构的失效柱点位移时程曲线如图3所示.

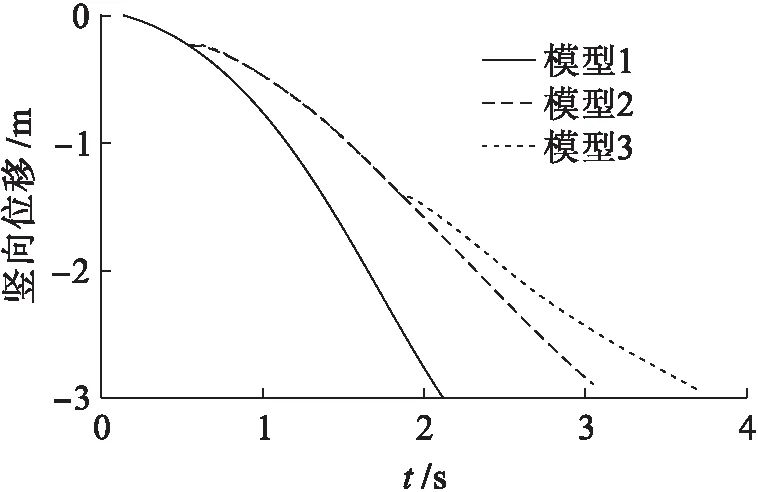
图3 失效柱点位移时程曲线Fig.3 Displacement time history curvesfor failed column points

由图3分析可知，当结构2层某角柱失效后，失效柱点的Z向位移随时间行进单调递增而未趋于稳定，说明选取的3个模型均发生了连续倒塌.另一方面，由图3中可以看出模型1(角柱与相邻边柱拉结)的位移发展最快，即曲线图最陡，随后是模型2(角柱另与相邻内柱拉结)，最平缓的为模型3(角部相邻边柱拉结)，这说明对角部承重构件的水平拉结能够在一定程度上限制倒塌时的竖向位移，但不同的拉结方案将产生不同的限制效果.模型2中角柱与相邻内柱对角拉结使得楼板荷载、两柱之间不平衡弯矩直接传导在该角柱上的内力增加；模型3中角柱相邻的边柱拉结冗余度增加，使得结构在角柱失效情况下能够形成新的角部支撑结构，代替原有结构破坏部分继续承载，但在继续增加荷载的情况下，结构最终趋向连续倒塌破坏.同时可看出，角柱周边的冗余约束越多，备用传力机制越复杂，结构的抗倒塌性能越好.

2.2 失效柱点内力分析

各模型失效层角部柱轴力分布如图4所示(F为轴力，M为轴力矩).

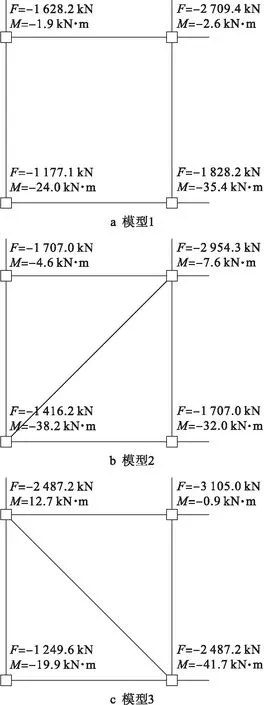
图4 结构失效层角部柱轴力Fig.4 Axial force of corner columnin structural failure layer

由图4可知，在角柱与相邻内柱拉结情况下，其对角部楼板荷载的传导起到了对角加载的作用，即楼面荷载主要由角柱与内柱承担，因此其角柱内力最大；在角柱周边有间接拉结情况下，角柱内力也比无拉结情况大.

值得注意的是，模型2及模型3相邻内柱、模型3相邻边柱的内力对比模型1均有所增加，这说明在结构角柱失效后，后两者相邻传力途径内力增加比没有拉结的模型1更多；在结构有冗余拉结情况下，结构的备用传力路径是否有效地承担工作，最直观的方式即考察该备用路径上的杆件内力是否增大，显然，模型2与模型3的计算结果可验证结构有效性.

2.3 结构抗倒塌性能分析

对3个模型的结构倒塌情况进行分析可知，在给定的荷载与荷载组合条件下，结构某角柱失效后，即发生倒塌，但其倒塌失效的时间有所不同.有拉结情况比无拉结情况的位移失效耗时更长，模型2、模型3分别比模型1增加了74%和52%.在失效内力方面，有拉结情况虽然比无拉结情况下角柱内力有所增大(模型2、模型3分别比模型1增加了16.9%和6.2%)，但相邻边柱和相邻内柱承载力、结构角部稳固性有所提升，间接增加了结构抗连续倒塌性能.

综合考虑结构失效后杆件的位移及内力响应(特别是角柱的轴力)后，分析如下：

1) 模型2的相邻边柱轴力相比模型1有所减少，但其角柱内轴力、相邻内柱轴力均有增加，特别是角柱内轴力增大了16.9%，这是因为角柱与相邻内柱对角拉结使得楼板荷载、两柱之间不平衡弯矩在该角柱上的内力增加，这种轴力增大是由于直接传导造成的(因为拉结梁的两端节点直接架设在失效柱柱点上)，综合考虑说明该方案不利于结构角柱失效情况，对于结构设计，应注意减少或不使用该种拉结方案.

3 结 论

在对本文建立的3个模型进行SAP2000非线性时程分析的基础上，分别研究了结构某角柱失效情况下的位移及内力情况.通过对模型1～3的失效后位移、轴力分析可看出，不同的结构方案在失效后的结构变形、倒塌时间及备用传力路径等方面均有不同.经本文计算分析得出如下结论：

1) 给定的有拉结情况虽然比无拉结情况下角柱内力有所增大，但相邻边柱与内柱承载力增加.

2) 在给定的荷载组合情况下，对角部竖向承重结构加以拉结，可在一定程度上增加结构抗连续倒塌性能，实现结构抗连续倒塌设计的目的.

参考文献(References)：

[1] Ellingwood B R.Mitigating risk from abnormal loads and progressive collapse [J].Journal of Performance of Constructed Facilities，2006，20(4)：315-323.

[2] 胡庆昌，孙金犀，郑琪.建筑结构抗震减震与连续倒塌控制 [M].北京：清华大学出版社，2005.

(HU Qing-chang，SUN Jin-xi，ZHENG Qi.Seismic damping and continuous collapse control of building structures [M].Beijing：Tsinghua University Press，2005.)

[3] Usmani A S.Stability of the world trade center twin towers structural frame in multiple floor fires [J].Journal of Engineering Mechanics，2005，131(6)：654-657.

[4] Ellingwood B R.Building design for abnormal loads and progressive collapse [J].Computer-aided Civil and Infrastructure Engineering，2005，20(3)：194-205.

[5] 罗跃纲，白玉艳.钢筋混凝土梁故障预测 [J].沈阳工业大学学报，2000，22(1)：66-68.

(LUO Yue-gang，BAI Yu-yan.Fault prediction of reinforced concrete beams [J].Journal of Shenyang University of Technology，2000，22(1)：66-68.)

[6] 中华人民共和国建设部.GB50011-2010 建筑抗震设计规范 [S].北京：中国建筑工业出版社，2010.

(The Ministry of Construction of the People’s Republic of China.GB50011-2010 The code for seismic design of building [S].Beijing：China Architecture & Building Press，2010.)

[7] 中华人民共和国建设部.GB50009-2012 建筑结构荷载规范 [S].北京：中国建筑工业出版社，2012.

(The Ministry of Construction of the People’s Republic of China.GB50009-2012 The load code for the design of building structures [S].Beijing：China Architecture & Building Press，2012.)

[8] 李易，陆新征，叶列平，等.钢筋混凝土框架抗连续倒塌机制研究 [J].建筑科学，2011，27(5)：12-18.

(LI Yi，LU Xin-zheng，YE Lie-ping，et al.Study on the progressive collapse mechanism of RC frame structures [J].Building Science，2011，27(5)：12-18.)

[9] 李易，陆新征，叶列平，等.基于Pushdown分析的RC框架抗连续倒塌承载力研究 [J].沈阳建筑大学学报(自然科学版)，2011，27(1)：10-18.

(LI Yi，LU Xin-zheng，YE Lie-ping，et al.Study on progressive-collapse resistance capacity of RC frame structures based on pushdown analysis [J].Journal of Shenyang Jianzhu University (Natural Science)，2011，27(1)：10-18.)

[10]袁波，曾明会，李霞昭.钢筋混凝土框架结构中次梁的抗连续倒塌性能分析 [J].沈阳建筑大学学报(自然科学版)，2014，30(1)：41-48.

(YUAN Bo，ZENG Ming-hui，LI Xia-zhao.Performance analysis of anti-progressive collapse of secondary beam in reinforced concrete frame structures [J].Journal of Shenyang Jianzhu University(Natural Science)，2014，30(1)：41-48.)

[11]陆新征，李易，叶列平，等.钢筋混凝土框架结构抗连续倒塌设计方法的研究 [J].工程力学，2008，25(增刊 2)：150-157.

(LU Xin-zheng，LI Yi，YE Lie-ping，et al.Study on design method to resist progressive collapse for reinforced concrete freames [J].Engineering Mechanics，2008，25(Sup2)：150-157.)

[12]王浩，李易，陆新征，等.基于倒塌率合承载力储备指标的结构抗连续倒塌能力评价方法 [J].建筑结构学报，2014，35(10)：65-72.

(WANG Hao，LI Yi，LU Xin-zheng，et al An evaluation method for progressive collapse resistance based on a collapse probability and a resistance reservation indexes [J].Journal of Building Structures，2014，35(10)：65-72.)