基于固定参数轨道的动态精密解算精度*

杨久东， 王文军， 孙 跃

(华北理工大学 矿业工程学院， 河北 唐山 063320)

高精度GPS动态测量定位在工程测量领域、基于安全的形变监测领域和军民用陆海空导航领域都有着广泛的应用.进行GPS动态精密解算的关键在于整周模糊度的估算和求解，常用的解算方法主要包括：基于观测值域的双频P码伪距法、基于坐标域的AMF模糊度函数法及基于最小二乘方法理论的LSAST法、LAMBDA法、FASF法、OMEGA法、FARA法等模糊度搜索法[1-4].上述方法的动态数据处理结果目前能够满足高精度工程测量的要求，但对于具有不确定时序特性的地震造成的地表位移实时形变监测数据处理不具备优势.

Track是麻省理工学院开发的GAMIT/GLOBK软件包中的一个动态双差定位模块，该模块利用双频P码伪距观测量和相位观测量组合(即“M-W”方法)求解宽巷模糊度，可以解算得到动态观测站每个历元的大地测量坐标和相对于参考站的坐标差，利用每个历元的结算数据就可以反演测站点的运动轨道.Track模块所选用的模糊度解算方法与基线长度无关，可有效地减小观测误差，精度较高.

Track解算过程需要一个相对稳定的固定站作为参考，通过该测站解算其它动态测站的单历元大地坐标，获取实际动态轨道[5-6].利用观测差值计算的重点是整周模糊度的求解，在得到正确的模糊度后，可得到流动站的选定坐标系.Track可以采用IGS数据中心提供的精密钟差和星历来消除影响GPS观测量精度的卫星钟差和轨道误差，而电离层和对流层延迟影响往往采用相关模型对其进行削弱.在处理数据过程中，利用卡尔曼滤波器对原始历元信息进行分析处理，再结合相应的消除模型消除流层延迟等相关误差，得到参数的估计值，用于以后的相关计算.在已经得到整周模糊度的情况下，还会利用其它技术(如平滑技术或者基线估计)将得到的参数重新带入，对初始历元在各个时刻的最佳状态进行最大的估计求解.

Track的定位模式包括L1、L2和LC三种模式.在一般情况下，当基线长度小于1 km时，可以使用单频的L1或L2定位模式，这时由于短基线两端观测环境具有极强的相关性，差分后会削弱电离层、对流层延迟；当基线长度大于1 km时，Track模块则会选择LC组合模式进行解算，此时的单频定位模式则不能对电离层延迟有效地消除，而LC组合可以基本消除电离层延迟误差.平台所提供的数据可按照一基准站、多流动站的原则对GPS数据同时进行处理，充分体现了Track在GPS动态数据解算处理应用中的优越性[7]，利用Track模块能够分析地震过程中基准站实时的位移变化情况[8-9].

1 实验操作

1.1 实验设计

为了验证Track模块在地震过程中对基准站实时位移的测量情况，本文设计了一个宽度为10 cm，高差最大为21 cm的动态轨道，实验轨道模型及场地如图1所示.利用GPS接收机进行高频数据采集，利用设计的轨道进行动态定位解算，并对Track解算结果精度进行了分析说明.

图1 实验轨道及实验场地Fig.1 Experimental orbit and site

轨道设计需要保证不会产生高差骤变，不会引起滑轮车倾斜或者跌落，并且保证安装有接收机的滑轮车能平稳运行.实验采用的接收机为Trimble R8 Model 3，接收机天线类型为TRM60158，对接收的采样率设置为1 Hz，卫星截止高度角设置为12°.

1.2 实验过程

选取较为开阔，没有明显遮挡的华北理工大学足球场作为模拟动态测量场地，试验场地的西南方向有几颗树，考虑到高度截止角设置为12°，树相对轨道模型来说在高度截止角以下，所以不存在遮挡干扰因素.

由于接收机实际是在设计轨道的中间运行，所以将设计轨道的中间轨道设定为理想轨道，将这条设计轨道与接收机真实轨道进行对比，分析其偏差和变化情况.在开阔场地分别选取距离为5、30、40 km作为基准点进行静态观测，并将3个测试点分别表示为Test1、Test2及Test3.在选好基准点后，对基准点进行标记命名，量取仪器高度，并利用接收机观测0.5 h左右.在开始观测的前5 min，将安装有接收机的小车平稳放置在轨道上方水平的位置，记作初始位置，目的在于使接收机能单点定位计算出大致坐标.静止5 min后，实验员沿着轨道按照顺时针方向移动小车，在移动过程中尽可能保持匀速且降低身体重心，以免对接收机信号接收造成干扰，且在不同观测站观测时均为同一实验员，这样可以减少不同实验员操作不统一而产生的误差.滑轮小车搭载接收机运行20 min后，将滑轮小车停滞在已经做好标记的初始位置，继续静态观测，观测5 min后，将多台接收机同时关机.

结束观测后，利用Trimble Data Transfer软件连接接收机，将观测好的数据文件导出，并利用Trimble Convert To RINEX软件将观测得到的T02文件格式转换成标准RENIX的O文件，再利用TEQC对转换好的O文件进行检验，查看信息是否完整.

1.3 精度评定点位选取

在确保得到的观测数据信息完全可以利用Track模块进行解算的情况下，将不同时间段观测的数据进行分组，分别利用不同距离的基站对校园内的流动站进行相对定位数据处理.为了方便检验，分别设置了几个观测点进行精度评定，分别为折点1、2、3、4，中点1、2、3、4，选取位置如图2所示.

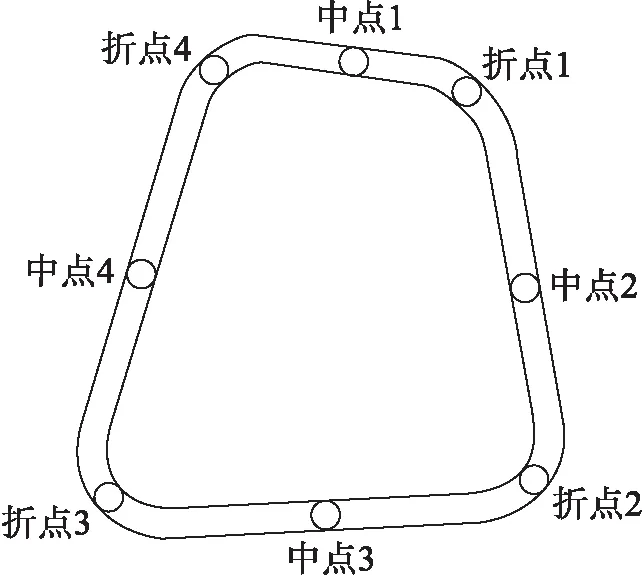
图2 精度评定点位选取Fig.2 Selection of accuracy assessment points

2 数据分析

在基站与流动站同步观测的前提下，采用相对定位原理计算出流动站的实时三维坐标，其处理模式分为AIR、SHORT和LONG三种，短基线处理精度达到毫米级，100 km以上的长基线精度也可达到厘米级.在应用Track软件处理数据时，虽然已经考虑了电离层折射改正、大气延迟改正等各种误差的影响，但是模糊度的快速解算与周跳的正确修复是必须要解决的两个问题.考虑到本次实验所用的基线较短，所以本次试验使用L1双差观测值组合来计算模糊度.L1载波相位观测值的波长较短，观测精度相对较高，就短基线而言，电离层延迟差对双差观测值的影响基本可以忽略，对流层延迟误差可采用Track模块中自带的模型进行减弱，所以选择短基线定位比较合理.本文利用快速星历对结果进行了对比分析，得到的实际运行轨道如图3所示.

2.1 水平数据分析

利用同一观测数据与IGS提供的两种星历(快速星历与精密星历)分别解算，并将结果进行对比.在快速星历下观测移动站和基准站相距约为5 km的Test1点位，观测数据经过分析处理 后，按照坐标位置导入到CAD图形中，其中点位较多的位置为初始时刻及转动结束后静止观测点位.按照同样的方法将相距为30 km的Test2和相距为40 km的Test3所解算坐标分布点在CAD中表现出来，如图4所示.

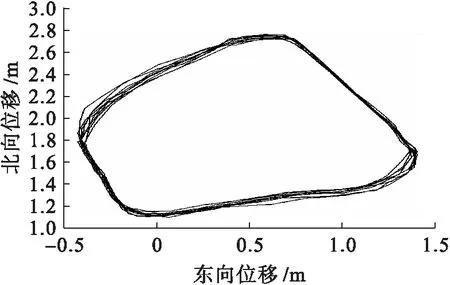
图3 运动轨道图Fig.3 Motion trajectory diagram

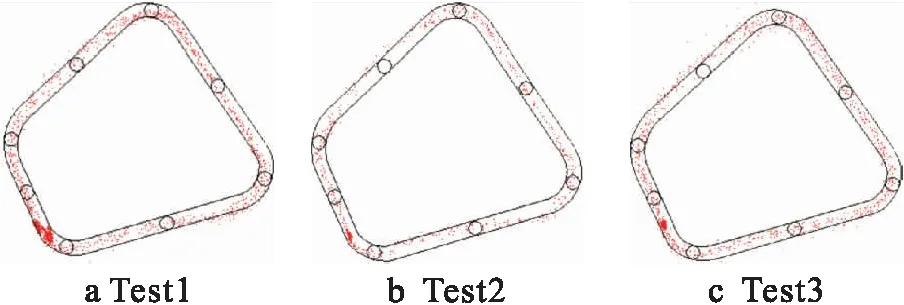
图4 不同基准站快速星历解算移动站的点位移

Fig.4Pointdisplacementofmobilestationsobtainedbyrapidephemeriscalculationfordifferentbasestations

将邻近观测数据间的平行线作为实际轨迹，对比实际轨迹与理想轨迹间的位移偏差如表1所示.

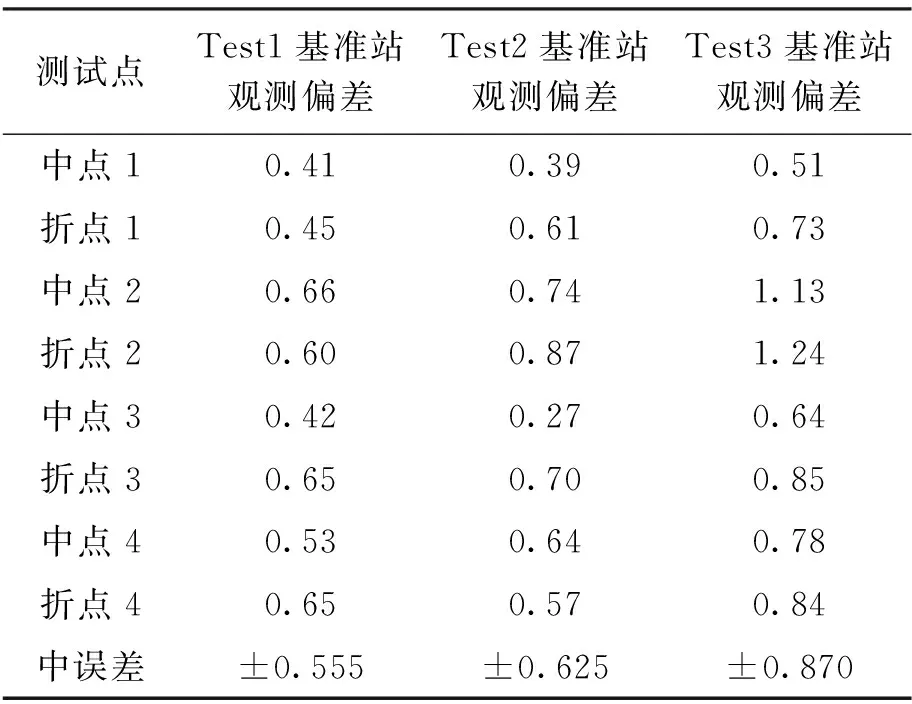
表1 快速星历解算的位移偏差Tab.1 Displacement deviation for rapidephemeris calculation cm

通过分析表1中的数据可以看出，距离最近的Test1基准站所产生的最大偏差值为0.66 cm，随着距离的增大，所得结果偏差也逐渐增大，Test2与Test3最大偏差值分别为0.87、1.24 cm，且不同距离的测站点所得到的中误差都小于±1 cm.最大偏差值控制在毫米范围内，符合利用GAMIT解算的精度.

按照同样的方法，利用精密星历对数据进行解算，得到不同基准站精密星历解算移动站的点位移如图5所示.

图5 不同基准站精密星历解算移动站的点位移

Fig.5Pointdisplacementofmobilestationsobtainedbyprecisionephemeriscalculationfordifferentbasestations

计算点位所在坐标与轨道中点的最大偏差值，得到对比结果如表2所示.

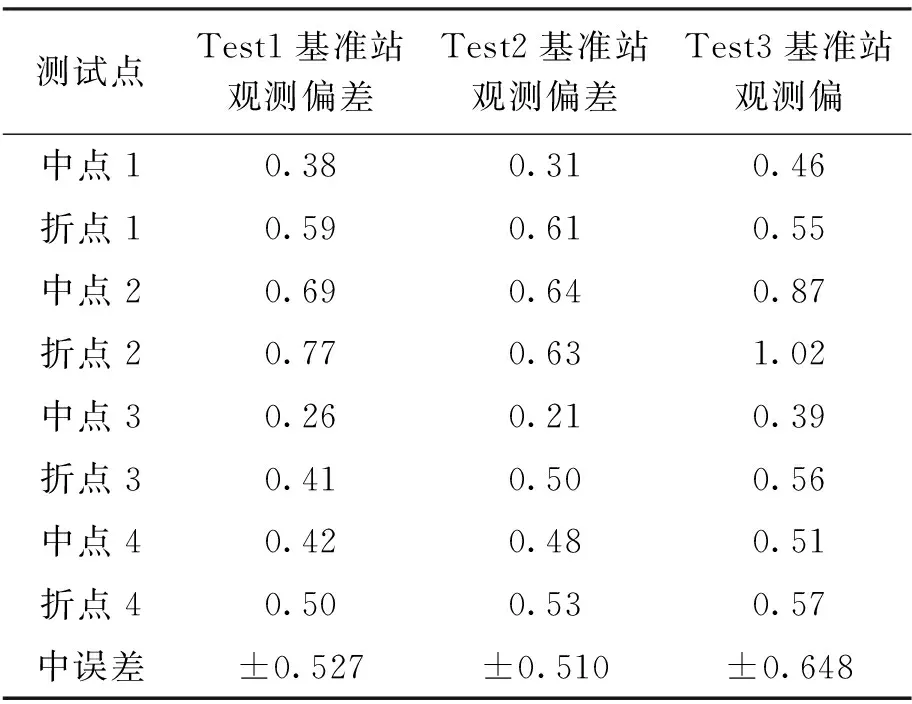
表2 精密星历解算的位移偏差Tab.2 Displacement deviation for precise ephemeriscalculation ephemeris calculation cm

在使用精密星历解算出来的结果中，除了第2个折点出现较大偏差外，相对于快速星历，在使用精密星历的情况下所得到的结果偏差较小，基本偏差都有了一定范围地减小.Test1最大偏差为0.77 cm，较快速星历解算结果变大，但是精度完全符合所解算的精度要求；Test2最大值为0.64 cm，较快速星历的0.87 cm有了0.23 cm的缩小；同样看出Test3最大值减少了0.22 cm，由1.24 cm变为1.02 cm，且不同距离测站所求得的中误差都有一定的减小，都小于±0.7 cm.

2.2 垂直数据分析

在已知利用精密星历分析得到的数据较为准确的前提下，同样利用Track模块和精密星历进行点位垂直方向变化分析，且应用在水平精度评定中.实验将经过同一点时动态接收机不同时刻的采样结果进行对比，并对Test1测站点的高差进行了分析.本文的高差是利用不同时刻在同一点的高程计算得到的，Test1共采集了8组数据，即接收机沿轨道运行了8周.

设计的实际轨道中点1为最低点，比轨道平面位置低13 cm(记为-13 cm)，中点4为设计的最高点，比轨道平面位置高8 cm(记为8 cm)，轨道面高度变化是渐变的，不存在骤升骤降情况.对采集的数据进行处理，得到最低点及最高点的8组位高差数据，结果如表3、4所示.

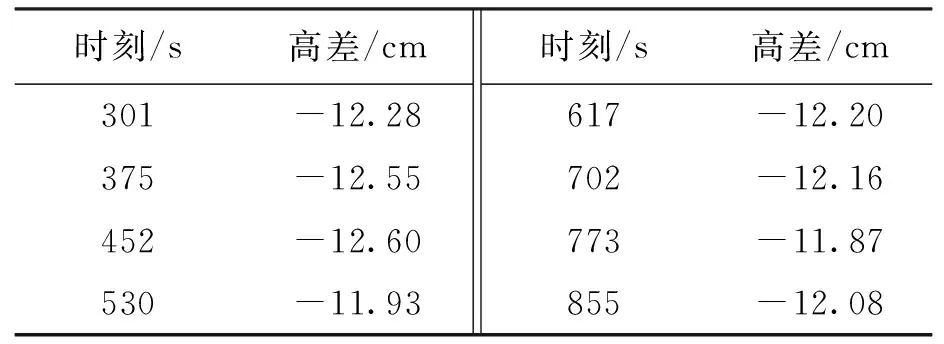
表3 最低点采样时刻及高差Tab.3 Sampling moments and height differenceinformation at lowest point

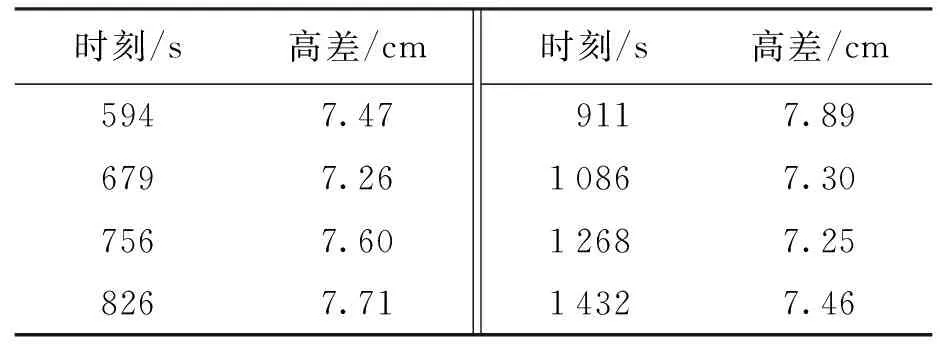
表4 最高点采样时刻及高差Tab.4 Sampling moments and height differenceinformation at highest point

由表3结果可知，轨道在最低点位的高差平均值为-12.21 cm，而轨道在设计时，设置参数的高度为-13 cm，所以偏差约为0.8 cm，属于毫米级精度；同样由表4结果可知，轨道在最高点位的高差平均值为7.5 cm，而轨道在设计时，设置参数的高度为8 cm，其偏差约为0.5 cm，也属于毫米级精度.

3 结 论

通过模拟实验对不同距离求得的坐标进行数据分析，得到动态接收机的运动轨道示意图.利用快速星历和精密星历对水平位置和垂直位置的精度进行了评定，水平和垂直方向的平均精度都可以满足动态测量的要求，充分体现了Track在GPS动态数据解算处理应用中的优越性.

实验结果表明，在数据量充足的情况下，该设计方案可以分析出地震发生时刻地震传播速度，并且根据监测站的位移变化得到地震的影响范围.今后工作主要将针对实现实验轨道的自动化，增强轨道的稳定性等方面进行，积极筹措基金支持，在地震易发地区布设连续运行观测站，力争为地震分析探索一条新渠道.

参考文献(References)：

[1] 刘经南，邓辰龙，唐卫明.GNSS整周模糊度确认理论方法研究进展 [J].武汉大学学报(信息科学版)，2014，39(9)：1009-1016.

(LIU Jing-nan，DENG Chen-long，TANG Wei-ming.Review of GNSS ambiguity validation theory [J].Geomatics and Information Science of Wuhan University，2014，39(9)：1009-1016.)

[2] 王德军，熊永良，刘宁，等.宽巷组合及轨道约束下的列车在轨动态单历元定位算法 [J].测绘学报，2014，43(2)：131-136.

(WANG De-jun，XIONG Yong-liang，LIU Ning，et al.Train on track kinematic single epoch positioning algorithm based on wide-lane combination and track constraints [J].Acta Geodaetica et Cartographica Sinica，2014，43(2)：131-136.)

[3] 祝会忠，刘经南，唐卫明，等.长距离网络RTK基准站间整周模糊度单历元确定方法 [J].测绘学报，2012，41(3)：359-365.

(ZHU Hui-zhong，LIU Jing-nan，TANG Wei-ming，et al.The algorithm of single-epoch integer ambiguity resolution between long-range network RTK base stations [J].Acta Geodaetica et Cartographica Sinica，2012，41(3)：359-365.)

[4] 李一鹤，沈云中，李博峰.基于LAMBDA方法的GPS动态相对定位 [J].测绘工程，2011，20(1)：6-10.

(LI Yi-he，SHEN Yun-zhong，LI Bo-feng.GPS kinematic relative positioning based on LAMBDA [J].En-gineering of Surveying and Mapping，2011，20(1)：6-10.)

[5] 熊永良，黄丁发，徐韶光，等.长距离动态GPS数据处理方法与汶川地震引起的动态地壳形变特征分析 [J].武汉大学学报(信息科学版)，2010，35(3)：265-269.

(XIONG Yong-liang，HUANG Ding-fa，XU Shao-guang，et al.Long distance kinematic GPS data processing and kinematic crustal deformation features analysis of Wenchuan Earthquake [J].Geomatics and Information Science of Wuhan University，2010，35(3)：265-269.)

[6] 周忠谟，易杰军，周琪.GPS卫星测量原理与应用 [M].北京：测绘出版社，2004.

(ZHOU Zhong-mo，YI Jie-jun，ZHOU Qi.Principle and application of GPS satellite measurement [M].Beijing：Surveying and Mapping Press，2004.)

[7] 苏小宁.高频GPS单历元定位方法及其在地震学中的应用研究 [D].北京：中国地震局地震预测研究所，2011.

(SU Xiao-ning.Study on high-rate epoch by epoch GPS positioning and its application in seismology [D].Beijing：Institute of Earthquake Forecasting，China Earthquake Administration，2011.)

[8] 殷海涛，肖根如，张磊，等.TRACK高频GPS定位中震时参考站的选取方法 [J].大地测量与地球动力学，2012，32(4)：15-19.

(YIN Hai-tao，XIAO Gen-ru，ZHANG Lei，et al.Study on method for selecting reference station in high rate GPS positioning using TRACK during earthquake [J].Journal of Geodesy and Geodynamics，2012，32(4)：15-19.)

[9] 韩凯，李亚东，王瑞云.小区域控制测量的GPS静态高程精度分析 [J].北京测绘，2012(6)：57-59.

(HAN Kai，LI Ya-dong，WANG Rui-yun.Analysis on small region static GPS height precision [J].Beijing Surveying and Mapping，2012(6)：57-59.)