基于支持向量机和卡尔曼滤波的机械零件剩余寿命预测模型研究
2018-06-06于震梁孙志礼曹汝男王鹏
于震梁, 孙志礼, 曹汝男, 王鹏
(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)
0 引言
准确预测机械装备中关键功能部件(如传动箱中的轴承、齿轮等)的剩余寿命既能保证设备在较高可靠性水平下工作,又可以避免过频(预防性)维修或更换造成的资源浪费。因此,在机械装备中关键部件的剩余寿命预测,越来越受到国内外工程师及学者关注。同时,传感器技术的快速发展及应用为航空航天、高速铁路运输、大型水面船舶等重要设备剩余寿命预测提供了必要的基础数据支撑,如某国内机床企业已在最新车床的主轴系统上安装振动传感器用于监测该系统运行状态,并开始制定基于设备状态数据的售后维护策略。
目前广泛应用的剩余寿命预测模型按采用的基本理论[1-2]可分为:统计和随机过程模型[3-4]、专家系统[5]、机器学习算法模型[6-9]及物理模型等。按建模时采用的训练数据来源可分为:基于全寿命状态退化数据的剩余寿命预测模型[6-8]和基于当前被预测零件退化轨迹的回归模型[9]。以支持向量机(SVM)[7,10-11]、相关向量机(RVM)[8-9]和神经网络[6]为代表的机器学习算法模型鲁棒性好,针对不同研究对象的建模过程差异较小,适应性强。
然而上述众多方法均致力于得到剩余寿命的点估计值,较少关注剩余寿命的其他统计特征(如一定置信度下的置信区间)。在基于可靠性的设备维护方案制定中,设备寿命概率分布情况对方案制定同样具有重要影响。基于全寿命状态退化数据的剩余寿命预测模型,根据全寿命试验等方法,获取具有研究对象整体统计特征的工作状态数据进行建模,得到零件运行状态与剩余寿命的映射关系,此类模型不能充分反映研究对象的个体差异。而基于当前零件退化轨迹的回归模型,在建模过程中过度依赖零件个体退化状态数据,当传感器受到较大外界干扰时,剩余寿命预测结果不够稳定。
为了弥补以上不足,借鉴交通流预测[12]、组合导航预测[13]、风电功率预测[14]等工程问题,本文提出了采用SVM和卡尔曼滤波相结合的实时预测模型建模思路,将SVM与非线性卡尔曼滤波模型相结合,构造出能够充分利用全寿命试验数据和被预测件个体实时状态退化数据的剩余寿命预测模型。所建立模型与现有SVM和卡尔曼滤波相结合的实时预测模型的不同之处在于,现有SVM和卡尔曼滤波相结合的实时预测模型将被预测对象(如:交通流、风电功率等)视为时间序列,即采用SVM建立时间序列预测模型,并采用卡尔曼滤波进行“修正”。本文所提出模型将全寿命试验数据中零件退化状态和对应的剩余寿命分别作为输出变量和输入变量的训练SVM模型,采用极大似然法估计SVM输出变量分布参数,并将所得SVM模型作为非线性卡尔曼状态更新方程,而并非为时间序列预测模型。SVM模型输出剩余寿命预测值只与给定时刻研究对象退化状态(如轴承振动信号)有关,与之前各时刻退化状态无关,即与退化过程无关;然后构造基于被预测件实时状态退化数据的时间更新方程,对研究对象剩余寿命进行修正,即考虑退化过程采用非线性卡尔曼滤波器对SVM所得剩余寿命预测值进行修正。设定初始剩余寿命点估计值及方差,通过逐步迭代计算各时刻零件剩余寿命值及一定置信水平下置信区间,从而实现所得剩余寿命预测值的同时又体现研究对象整体退化特性以及被预测件的个体差异。
1 理论基础
1.1 剩余寿命
机械零件从开始工作至失效大致经历3个阶段:稳定运行、性能持续退化、最终失效。在第1阶段其各项性能指标不会有明显变化,在初始损伤后随工作时间变长会有退化发生且逐渐加剧,当退化量达到或超过某一极限时零件最终失效。若某零件t时刻退化程度可由指标x(t)度量(x可为矢量也可为标量,此处以标量为例进行说明),不失一般性,可设x(t)呈递增趋势,当x(t)达到或超过预设阈值[x]时,认为该零件无法完成指定功能即失效,则t时刻该零件的剩余寿命为RUL(t)=inf{t1|x(t1)≥[x]}-t,inf{}表示下确界。
1.2 SVM理论
SVM是一种以统计学习理论为基础、以结构风险最小化为原则的机器学习算法,广泛应用于模式识别、故障诊断、结构可靠性分析、回归分析等领域。本文中采用SVM进行机械零件剩余寿命预测。
若训练样本为S={(vn,yn),vn∈Rl,yn∈R,n=1,2,…,N},vn为l维输入变量(l≥1),yn为与vn对应的输出变量,n为训练样本数。为了构造结合SVM和卡尔曼滤波的剩余寿命预测模型,将输入变量和输出变量分别设定为剩余寿命值和零件退化特征量。
当y与v为线性关系时,
f(x)=w·v+b,
(1)
式中:f(x)为对应输出变量y的回归函数;w∈Rl为权值矢量;b∈R;w·v表示w与v间的点积。
w和b可通过如下优化问题求得:
(2)

(3)
(4)
当v与y为非线性关系时,可通过满足Mercer条件的核函数将该非线性问题转为更高维度的线性问题。此时只需将(4)式中vn·v替换为K(vn,v),(4)式回归函数可变为
(5)
式中:K(·,·)为核函数。本文取K(·,·)为应用最广泛的高斯径向基核函数,形式为K(vm,vn)=exp(-γ‖vm-vn‖2),γ为核函数参数。
给定训练样本S、惩罚因子C及核函数参数γ对SVM模型精度和推广能力有很大影响,采用K-fold交叉验证法[16]确定最优(C,γ)组合,实例分析中取K=10.
2 基于SVM和卡尔曼滤波的剩余寿命预测模型
2.1 SVM输出变量分布估计
y=(v)+ζ,
(6)
式中:ζ为零均值残差项。假设v与ζ相互独立,则该假设在理论上是不成立的,但工程中依据此假设计算所得出的输出变量y的概率分布所产生误差,在可接受范围内[17]。
根据文献[17],通常情况下ζ服从拉普拉斯分布或零均值正态分布。本文中取后者,即假设ζ服从零均值正态分布,方差为σ2. 随机变量ζ的N个观测值为ζn=yn-(vn),则σ2的极大似然估计可表示为
(7)
结合(6)式,可得SVM模型输出变量y的近似服从均值和方程分别为(v)和2的正态分布,
y~N((v),2),
(8)
因此,
P(|y-(v)|≤3)≈0.997 3.
(9)
2.2 结合SVM和卡尔曼滤波的剩余寿命预测模型
全寿命状态数据的剩余寿命预测模型其基本思想是,充分利用了全寿命试验数据建立寿命预测模型,所建立模型能够体现研究对象的共性特征(如性能退化曲线走向),而缺乏对个体对象工作环境或载荷特性的反映(如由于制造、安装随机误差、承受载荷等造成的个体差异)。这是基于当前被预测零件退化轨迹的剩余寿命预测模型建模过程不需要全寿命试验数据,且能够反映个体差异,但缺乏对同类或相似产品的“共性认识”。
下面提出构造SVM与非线性卡尔曼滤波相结合的剩余寿命预测模型。首先,使用经过整理的研究对象的全寿命试验数据或相似产品退化数据训练SVM模型,即:tn时刻零件剩余寿命RUL(tn)作为SVM输入变量,将退化指标x(tn)作为输出变量,通过K-fold交叉验证法确定最优(C,γ)组合,将所得SVM模型(RUL)作为非线性卡尔曼滤波模型的状态更新方程。然后,基于被预测件实时状态退化数据构造时间更新方程,从而达到所得剩余寿命预测模型既能够利用全寿命数据(SVM模型)又考虑到研究对象个体差异(卡尔曼滤波模型)的目的。综上所述,本文构造的剩余寿命预测模型可表示为
RULn=RULn-1-Δn-1,n,Δn-1,n=tn-tn-1,
(10)
xn-1=(RULn-1)+ζ,ζ~N(0,2),
(11)
式中:RULn为tn时刻剩余寿命;xn为tn时刻退化指标取值。
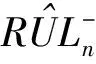
(12)式和(13)式为所提模型基本思想的数学表示:
(12)
(13)
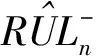
(14)式和(15)式分别为基于全寿命状态退化数据的剩余寿命预测模型和基于当前被预测件退化轨迹的回归模型基本思路的数学表示:
(14)
(15)
由(12)式和(13)式及图1可知,应用(10)式和(11)式模型得到的零件剩余寿命预测值整合了相同或相似产品退化数据和被预测零件各时刻工作状态观测值,最大限度地利用了已知数据。
2.3 所提出模型迭代求解


4)根据卡尔曼滤波模型及SVM输出变量分布特性可知,RULn真实值服从正态分布:
(16)
3 基于SVM的轴承剩余寿命预测
采用美国国家基金会产学研合作中心IMS(Inteligent Maintenance Systems)数据库中滚动轴承全寿命试验数据[18]验证本文提出剩余寿命预测模型准确性及稳定性。该滚动轴承试验采用美国莱克斯诺工业集团ZA-2115双列滚动轴承组成。试验转速为2 000 r/min,各轴承所承受径向载荷约为27 kN. 加速度传感器安装在轴承座上,每隔10 min采集一次数据,每次采集时长为1 s,收集20 480个加速度值。
借鉴文献[19]中均方根(RMS)值的方法,求解方均根uRMS如(17)式所示,
(17)
式中:un(i)(i=1,…,T)为第n次信号序列;T为每次信号采集数据点个数。RMS对个体差异敏感,需要对RMS进行标准化和滑移平均处理。首先选取正常期内一段趋势平稳RMS,将该段RMS平均数定为标准值。随后计算原始RMS与标准值之比,得到相对均方根(RRMS)值. 为减少振动特征随机性的影响,利用7点滑移平均处理RRMS,得到平滑的RRMS.
选用平滑的RRMS值作为轴承退化程度度量。RRMS值越大,说明振动越强烈,工作状态退化越严重。图2为平滑处理后试验中2号、3号、4号轴承RRMS值随时间变化情况。定义轴承退化起始阈值和最终失效阈值分别为1.05和1.50,即当RRMS值处在1.05和1.50之间时认为轴承处于性能退化阶段,当RRMS值达到或超过1.50时轴承失效。由于稳定工作阶段的轴承各项振动指标没有明显波动,难以建立模型进行剩余寿命预测,只对处于退化阶段的剩余寿命值进行预测说明。根据所设置衰退起始阈值2号、3号、4号轴承的起始衰退时间分别约为开始工作后100 h、103 h和118 h(见图2),3个滚动轴承进入衰退期后RRMS与RUL(t)值组成的样本集分布为S2、S3、S4.S2={(RUL2,n,x2,n),n=1,2,…,146},S3={(RUL3,n,x3,n),n=1,2,…,148},S4={(RUL4,n,x4,n),n=1,2,…,126}。
设不敏感因子ε=0,将S2作为验证集,用于验证所提出方法的准确性,S3∪S4作为训练集(是SVM模型所需的),用于训练所构造的剩余寿命预测模型,采用10-fold交叉验证度量SVM精度及推广能力,在二维空间优化(C,γ),得到最优参数为=3.66,=15.71. 再根据1.2节理论训练SVM模型,并依据(7)式估计所得模型输出残差项方差,2=1.6×10-3. 由数据采集间隔值可知,Δn,n+1=1/6.
令P0=(0.1RUL0)2,P0为2.2节中剩余寿命预测模型的初始条件之一(亦为非线性卡尔曼滤波的初始条件之一),进入退化阶段时2号轴承剩余寿命RUL0=24.5 h(即该轴承进入退化阶段运行24.5 h后完全失效,见图3),为了验证基于SVM和卡尔曼滤波的剩余寿命预测模型准确性,在模型中设定进入退化阶段时2号轴承剩余寿命RUL0值与真实值应有一定偏差。当模型初始条件RUL0=18 h时,应用2.3节中迭代方法求解,得到衰退期轴承各时刻的剩余寿命均值,以及在置信水平为0.997 3的剩余寿命置信区间上下限曲线,并与真实值对比,如图3(a)所示。图3(b)、图3(c)、图3(d)分别为RUL0取值20 h、23 h、25 h时,进入退化阶段的轴承在各时刻剩余寿命均值和上下限曲线与真实值的对比情况。
由图3可知,基于SVM和卡尔曼滤波的剩余寿命预测模型能够较准确地预测轴承在各时刻的剩余寿命,且置信水平为0.997 3的剩余寿命置信区间较好地覆盖了真实剩余寿命值。当RUL0与真实值存在较大偏差时(见图3(a)和图3(b)),该模型能够逐步修正剩余寿命预测值,缩小预测误差,使其逐渐接近真实值。当RUL0与真实值较接近时(见图3(c)和图3(d)),各时间点处剩余寿命预测值总体上在真实剩余寿命附近波动。
4 结论
本文通过分析基于全寿命状态数据的剩余寿命预测模型和基于当前被预测件退化轨迹的剩余寿命预测模型存在的不足,提出了将SVM与非线性卡尔曼滤波相结合的剩余寿命预测模型。该模型的特点为:1)将现有试验数据训练所得SVM模型作为卡尔曼滤波状态更新方程,剩余寿命预测值是基于已掌握的全寿命试验数据以及被预测件衰退期内退化信号所得到的,最大限度利用了各类数据;2)能够提供剩余寿命值的区间估计;3)模型中只假设研究对象工作状态随时间存在退化特性,因此具有一定的通用性。
通过滚动轴承的实例分析,得到以下结论:1)本文提出的方法能够较准确地预测处于退化阶段零件的剩余寿命;2)置信水平为0.997 3的剩余寿命置信区间大多数情况下包含真实剩余寿命值,有效地弥补了模型可能存在的误差。3)当初值与真实值存在较大误差时,能够通过迭代逐步改善预测值精度,但当RUL0相对误差过大时(如大于15%甚至20%),会导致剩余寿命预测值收敛于真实值的速度变慢,RUL0准确性对模型的预测精度较重要。因此,本文提出的方法可以为制定合理的设备维护策略提供参考,也可为解决工程中的类似问题提供借鉴。
参考文献(References)
[1] Tsui K L, Chen N, Zhou Q, et al. Prognostics and health management: a review on data driven approaches[J]. Mathematical Problems in Engineering, 2015(6): 1-17.
[2] Kan M S, Tan A C C, Mathew J. A review on prognostic techniques for non-stationary and non-linear rotating systems[J]. Mechanical Systems and Signal Processing, 2015, 62/63:1-20.
[3] Hong T P, Yang B S. Estimation and forecasting of machine health condition using ARMA/GARCH model[J]. Mechanical Systems and Signal Processing, 2010, 24(2):546-558.
[4] Lei Y G, Li N P, Lin J. A new method based on stochastic process models for machine remaining useful life prediction[J].IEEE Transactions on Instrumentation and Measurement, 2016, 65(12):2671-2684.
[5] Sanders D A, Graham-Jones J, Gegov A. Improving ability of tele-operators to complete progressively more difficult mobile robot paths using simple expert systems and ultrasonic sensors[J]. Industrial Robot, 2010, 37(5):431-440.
[6] Malhi A, Yan R, Gao R X. Prognosis of defect propagation based on recurrent neural networks[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3):703-711.
[7] Kim H E, Tan A C C, Mathew J, et al. Bearing fault prognosis based on health state probability estimation[J]. Expert Systems with Applications, 2012, 39(5):5200-5213.
[8] Caesarendra W, Widodo A, Yang B S. Application of relevance vector machine and logistic regression for machine degradation assessment[J]. Mechanical Systems and Signal Processing, 2010, 24(4):1161-1171.
[9] Zio E, Maio F D. Fatigue crack growth estimation by relevance vector machine[J]. Expert Systems with Applications, 2012, 39(12):10681-10692.
[10] Sun F Q, Li X Y, Jiang T M, et al. A Bayesian least-squares support vector machine method for predicting the remaining useful life of a microwave component[J].Advances in Mechanical Engineering, 2017, 9(1): 1-9.
[11] Maior C B S, Moura M D C, Lins I D, et al. Remaining useful life estimation by empirical mode decomposition and support vector machine[J]. IEEE Latin America Transactions, 2016, 14(11):4603-4610.
[12] 朱征宇, 刘琳, 崔明. 一种结合SVM与卡尔曼滤波的短时交通流预测模型[J]. 计算机科学, 2013, 40(10):248-251.
ZHU Zheng-yu, LIU Lin, CUI Ming. Short-term traffic flow forecasting model combining SVM and Kalman filtering [J]. Computer Science, 2013, 40(10): 248-251. (in Chinese)
[13] 陈磊琛. 支持向量机与卡尔曼滤波算法在组合导航中的应用研究[D]. 武汉:中国地质大学, 2010.
CHEN Lei-chen. Research on support vector machine and its application in integrated navigation with Kalman filter [D]. Wuhan:China University of Geosciences, 2010. (in Chinese)
[14] 杨茂, 黄宾阳, 江博,等. 基于卡尔曼滤波和支持向量机的风电功率实时预测研究[J]. 东北电力大学学报, 2017, 37(2):45-51.
YANG Mao, HUANG Bin-yang, JIANG Bo, et al. Real-time prediction for wind power based on Kalman filter and support vector machines [J]. Journal of Northeast Electric Power University,2017, 37(2):45-51. (in Chinese)
[15] Kjeldsen T H. A contextualized historical analysis of the Kuhn-Tucker theorem in nonlinear programming: the impact of World War II[J]. Historia Mathematica, 2000, 27(4):331-361.
[16] 刘学艺,李平,郜传厚. 极限学习机的快速留一交叉验证算法[J]. 上海交通大学学报, 2011, 45(8): 1140-1145.
LIU Xue-yi, LI Ping, GAO Chuan-hou. Fast leave-one-out cross-validation algorithm for extreme learning machine[J]. Journal of Shanghai Jiao Tong University, 2011, 45(8): 1140-1145. (in Chinese)
[17] Lin C J, Weng R C. Simple probabilistic predictions for support vector regression[R]. Taipei: National Taiwan University, 2004.
[18] Qiu H, Lee J, Lin J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]. Journal of Sound & Vibration, 2006, 289(4):1066-1090.
[19] 申中杰,陈雪峰,何正嘉,等. 基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J]. 机械工程学报,2013,49(2):183-189.
SHEN Zhong-jie, CHEN Xue-feng, HE Zheng-jia, et al. Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine [J].Journal of Mecha-nical Engineering, 2013, 49(2): 183-189. (in Chinese)
