校园开放对周边道路通行能力的影响

林巧儿 甘宇 周艳 郑欣 廖金钰

摘 要：本文通过问卷调查找出影响道路通行能力的主要因素，构建评价指标体系，运用层次分析法对各指标进行综合评定。运用熵权法确定校园开放前后各指标值权重，进而计算出学校开放前后投影值，并提出缓解交通拥堵的合理化建议。

关键词：评价指标体系 层次分析法 熵权法 投影值

中图分类号：F293.3 文献标识码：A 文章编号：1672-3791（2018）01（a）-0012-02

该校在前后两校门口设立了车辆进出门禁系统，减轻了校内的通行压力，同时也会对周边道路通行能力产生影响，我们针对校园开放前后对交通影响的不同进行了研究。本文通过问卷调查找到影响道路通行能力的主要因素，运用层次分析法对各指标进行综合评定。构造封闭型和开放型方形校园模型，计算校园开放前后各指标及投影值，比较两者得出校园开放后对周边道路通行能力的影响更大且有助于解决周边交通拥堵问题。

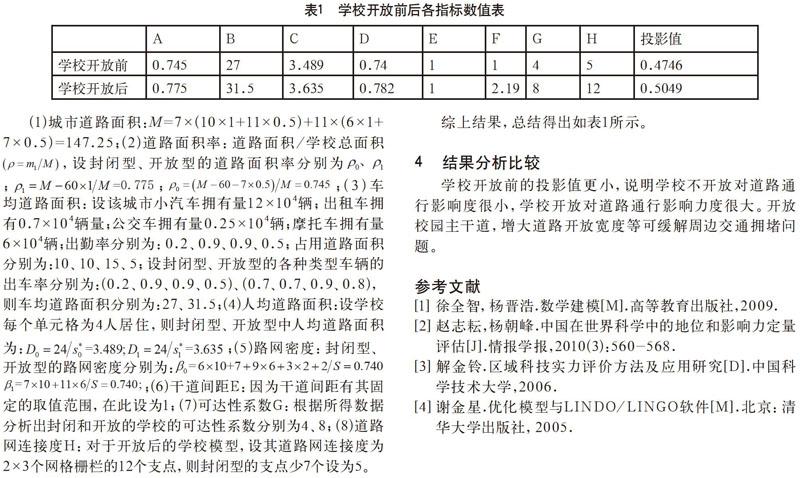
3 学校开放前后各指标值及投影值

将学校方格网络化后，学校实质就归结为封闭型和开放型方格网络结构如下所示，将学校看作由6×10个单位面积的组成的区域，学校由6个单位面积和宽度为0.5个单位的路网组成的区域组成。本文将问题归结为封闭和开放两方面，并计算各项指标的具体值，见圖2，图3。

（1）城市道路面积：M=7×（10×1+11×0.5）+11×（6×1+7×0.5）=147.25；（2）道路面积率：道路面积/学校总面积，设封闭型、开放型的道路面积率分别为；；；（3）车均道路面积：设该城市小汽车拥有量12×104辆；出租车拥有0.7×104辆量；公交车拥有量0.25×104辆；摩托车拥有量6×104辆；出勤率分别为：0.2、0.9、0.9、0.5；占用道路面积分别为：10、10、15、5；设封闭型、开放型的各种类型车辆的出车率分别为：（0.2、0.9、0.9、0.5）、（0.7、0.7、0.9、0.8），则车均道路面积分别为：27、31.5；（4）人均道路面积：设学校每个单元格为4人居住，则封闭型、开放型中人均道路面积为：；（5）路网密度：封闭型、开放型的路网密度分别为：；（6）干道间距E：因为干道间距有其固定的取值范围，在此设为1；（7）可达性系数G：根据所得数据分析出封闭和开放的学校的可达性系数分别为4、8；（8）道路网连接度H：对于开放后的学校模型，设其道路网连接度为2×3个网格栅栏的12个支点，则封闭型的支点少7个设为5。

综上结果，总结得出如表1所示。

4 结果分析比较

学校开放前的投影值更小，说明学校不开放对道路通行影响度很小，学校开放对道路通行影响力度很大。开放校园主干道，增大道路开放宽度等可缓解周边交通拥堵问题。

参考文献

[1] 徐全智，杨晋浩.数学建模[M].高等教育出版社，2009.

[2] 赵志耘，杨朝峰.中国在世界科学中的地位和影响力定量评估[J].情报学报，2010（3）：560-568.

[3] 解金铃.区域科技实力评价方法及应用研究[D].中国科学技术大学，2006.

[4] 谢金星.优化模型与LINDO/LINGO软件[M].北京：清华大学出版社，2005.